Собственная частота механической системы с распределенными параметрами без демпфирования

В качестве первой технической системы рассмотрим поперечную вибрацию участка трубопровода между двумя опорами.

Любая расчетная схема технической системы определяется набором принимаемых во внимание (учитываемых в расчете) силовых факторов и математической моделью, идеализирующей реальную механическую систему. Определение набора действующих на трубопровод силовых факторов и их количественных величин является самостоятельной сложной задачей, выходящей за пределы нашего курса. В качестве же математической модели трубопровода могут быть использованы трехмерная постановка, двухмерная (та или иная теория оболочек) и одномерная (обычно называемая балочной или стержневой). Выбор математической модели определяет набор учитываемых в расчете или отбрасываемых компонент тензора напряжений материала трубы. Количественной характеристикой, определяющей отношение отбрасываемых и учитываемых компонент и, следовательно, границ применения математических моделей, является характерный масштаб изменения деформаций. В данной задаче этим характерным масштабом является длина полуволны поперечной вибрации трубопровода. Пока для упрощения вычислений в качестве расчетной схемы трубопровода примем балочную (стержневую) теорию, то есть будем рассматривать ситуацию, когда длина полуволны вибрации трубопровода превышает диаметр трубы больше, чем на порядок.

Будем также пока считать, что трубопровод совершает вибрацию при отсутствии внешней нагрузки и демпфирования, то есть совершает свободные колебания под воздействием собственного веса и сил упругой реакции материала трубы. В рамках принятой расчетной схемы уравнение движения незагруженного трубопровода имеет вид

,

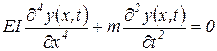(26)

где 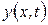- функция перемещения нейтральной оси трубопровода;

х - координата, отсчитываемая по оси трубопровода от левой опоры;

Е - модуль Юнга материала трубы;

I - момент инерции поперечного сечения трубы;

EI - жесткость поперечного сечения трубы;

m - суммарная масса единицы длины трубопровода;

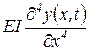- сила упругой реакции материала трубы;

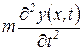- сила инерции суммарной массы трубопровода.

После введения безразмерной координаты 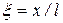(l - длина трубопровода - балки между опорами) уравнение (26) примет вид

,

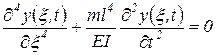(27)

Таким образом получили дифференциальное уравнение в частных производных по безразмерной координате x и времени t относительно неизвестной функции перемещения нейтральной оси трубопровода y=y(x,t).

Согласно методу разделения переменных Фурье общее решение уравнения (27) с учетом (23) может быть получено в виде (демпфиро­вание не учитывается, поэтому а=0)

,

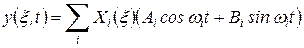(28)

в котором 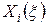являются ортогональными фундаментальными функциями, отвечающими условию

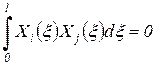при .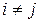

После подстановки (28) в уравнение (27) получим для каждой функции 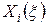обыкновенное дифференциальное уравнение (индекс i опускаем)

,

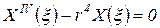(29)

где

.

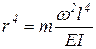(30)

Решение уравнения (29) будет иметь вид

.

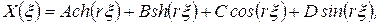(31)

которое удобно записать в виде

.

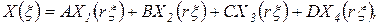(31)

где

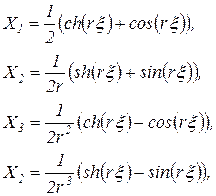
Обычно функции 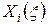(i=1,...,4) называют функциями Крылова. произвольные постоянные А, В, С и D определяются из граничных условий. Эти условия могут быть, например, следующими:

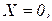
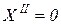для x = 0 и x = 1 – шарнирно опертый конец,

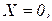
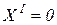для x = 0 и x = 1 – жестко заделанный конец,

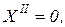
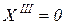для x = 0 и x = 1 – свободный конец,

Как видно из (31), функции формы в качестве аргумента содержат безразмерную координату x и величину r = r(w). Таким образом, функции формы зависят от соответствующих им собственных частот.

Из (30) получаем зависимость угловой частоты собственных колебаний трубопровода-балки:

.

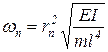(32)

где n ‑ номер формы вибрации (n = 1,2,3,...).

Значения угловой частоты зависят от коэффициента r_n, величина которого определяется в зависимости от условий закрепления и формы колебаний:

идеальный шарнир в обеих опорах: r_n = rp (n=l,2,3,...);

идеально жесткое закрепление в обеих опорах:

r₁ = 4,73,

r₂ = 7,8532,

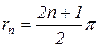при n³3.

Таким образом, одной из характеристик механической системы является собственная частота (спектр собственных частот), величина которой зависит от жесткости, массы, геометрических размеров и условий закрепления системы. Возможный диапазон изменения собственной частоты при изменении ее аргументов определяется для каждого конкретного случая.