Фазовая и частотная модуляции гармонической несущей

Определение и параметры. При фазовой модуляции отклонение (сдвиг) фазы модулированного сигнала от линейной ω₀t+ψ₀ изменяется пропорционально мгновенным значениям мо­дулирующего сигнала u_M(t)

ψ(t)= ω₀t+ψ₀+Δφ_дu_M(t), (3.12)

где Δφ_д — коэффициент пропорциональности, называемый девиа­цией фазы (от лат. deviatio — отклонение). Физический смысл этого коэффициента поясняется рис. 3.7, где изображены модули­рующий сигнал и полная фаза ФМ сигнала. С увеличением сиг­нала u_M(t) полная фаза ψ(t) растет во времени быстрее, чем по линейному закону. При значениях сигнала u_M(t)<.0 происходит спад скорости роста ψ(t) Абсолютная величина отклонения (сдвига) фазы от линейной наибольшая, когда и_м(0 достигает экстремальных значений. На рис. 3.7,б отмечено максимальное от­клонение фазы вверх Δφ₊ и вниз Δφ_- Наибольшее отклонение фазы от линейной и является девиацией фазы Δφ_д при ФМ. В при­мере рис. 3.7 Δφ_д= Δφ₊ Измеряется Δφ_д в радианах и может при­нимать значение от единиц до десятков тысяч радиан.

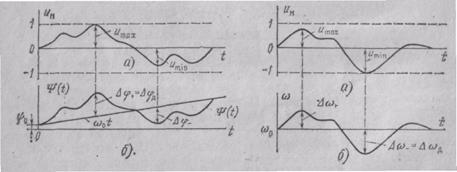
Рис. 3.7. Полная фаза ФМ сигнала. Рис. 3.8. Мгновенная частота ЧМ

а — модулирующий сигнал; б — измене- сигнала:

ние полной фазы а-модулирующий сигнал; б - из-

менение мгновенной частоты

Подставляя (3.12) в (3.1), получаем аналитическое выражение (математическую модель) ФМ сигнала:

S_фм(u_м,t)=A₀cos[ω₀t+ψ₀+Δφ_дu_м(t)]. (3.13)

При частотной модуляции отклонение частоты модулированно­го сигнала от ш₀ изменяется пропорционально мгновенным значе­ниям модулирующего сигнала u_u(t)

ω(t)=ω₀+Δω_дu_м(t) (3.14)

где Δω_д — коэффициент пропорциональности.

По аналогии с ФМ коэффициент Δω_д называют девиацией час­тоты и она равна наибольшему отклонению частоты модулирован­ного сигнала от значения частоты несущей ω₀ Изменение частоты ЧМ сигнала графически показано на рис. 3.8, где отмечена девиа­ция частоты Δω_д соответствующая наибольшему отклонению час­тоты вниз Δω_д=Δω_- поскольку Δω₊=Δω_- Как и при ФМ, в вы­ражении (3.14) величина u_u(t) нормирована, т. е.

Девиация частоты является одним из главныхпараметров частотных модуляторов и может принимать значения от единиц герц до сотен мегагерц в модуляторах различного назначения. Однако всегда необходимо, чтобы выполнялось условие

Полную фазу ЧМ сигнала с частотой (3.14) согласно (3.3) на­ходим путем интегрирования, т. е.

ψ_чм(t)=∫ω(t)dt=∫[ ω₀+Δω_дu_м(t)]dt= ω₀t+Δω_д∫ u_м(t)dt+Ψ₀,

где ψ₀ можно рассматривать как постоянную интегрирования. Тогда аналитическое выражение (математическая модель) ЧМ сигнала запишется в виде

S_ЧМ(u_м,t)=A₀cos[w₀t+Ψ₀+Δω_д∫u_м(t)dt[. (3.15)

Поскольку u_u(t) входит з это выражение под знаком интеграла, ЧМ часто называют интегральным видом модуляции.

Однотональные сигналы с угловой модуля­цией. При модуляции одним тоном(u_м,t)=cos(Ωt+Ψ) с уче­том того, что ∫cosax=(1/a)sinax, из (3.13) и (3.15) получаем, что аналитические выражения ФМ и ЧМ сигналов по форме за­писи имеют совершенно одинаковый вид

S_фм(u_м,t)=A₀cos[ω₀t+ψ₀+m_фмcos(Ωt+Ψ)];

S_чм(u_м,t)=A₀cos[ω₀t+ψ₀+m_чмsin(Ωt+Ψ)], (3.16)

где m — индекс модуляции. Отличие только в порядке вычисления индекса и фазы модулирующего колебания. При ФМ индекс мо­дуляции m_ФМ — величина, равная девиации фазы модулированно­го сигнала при гармоническом модулирующем сигнале u_M(t), т. е. m_ФМ —Δφ_д. При ЧМ индекс модуляции m_ФМ— отношение девиа­ции частоты модулированного сигнала Δω_д=2πΔf_д к частоте мо­дулирующего гармонического сигнала Ω=2πF т. е. m_чм=Δω_д/Ω

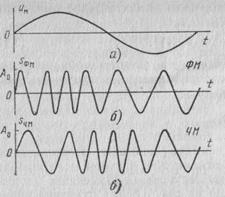
Рис. 3.9. Временные диаграммы угло­вой модуляции:

я — модулирующий гармонический сигнал; б — фазовая иодуляция; в — частотная модуляция

= Δf_д/F- Следовательно, ин­декс частотной модуляции яв­ляется амплитудой отклонения фазы, измеренной в радианах. Из (3.13), (3.15) и (3.16) следует, что частотно-модули­рованный сигнал является в то же время и фазо-модулирован- ным. Справедливо и обратное утверждение, поэтому ЧМ и ФМ в общем случае являются разновидностями угловой модуляции гармснической несущей. При гармоническом модулирующем сигнале временные диа­граммы ФМ и ЧМ имеют совершенно одинаковый вид (рис. 3.9). Отличить их можно, только сравнив изменение мгно­венной фазы модулированного сигнала с законом изменения модулирующего колебания. Особенности ФМ и ЧМ при гармони­ческом модулирующем сигнале отражены в табл. 3.2, где приме­няются принятые ранее обозначения, а — коэффициент пропор­циональности.

Пример 3.3. Дана реализация модулированного сигнала

s(u_m,t)=10cos(10⁷t+5sin2*10³t).

Указать вид модуляции и информационный параметр. Определить ампли­туду и частоту несущей, частоту модулирующего сигнала, характеристики мо­дулированного.

Из сравнения аналитического выражения модулирозанного сигнала с урав­нениями (3.16) следует, что это однотональная угловая модуляция (ЧМ или ФМ—определить нельзя). Информационный параметр модуляции — полная фа­за несущей s_н(t) = 10 cos 10⁷t

Амплитуданесущей А₀=10 В, угловая частота ω₀=10⁷ рад/с. Угловая час­тота модулирующего сигнала Ω=2• 10³ рад/с. Параметры модуляции: индекс т=5; девиация фазы Δφ_д=5 рад; девиация частоты Δω_д=mΩ =10-10³ = 10⁴ рад/с.

Спектр при угловой модуляции. Сигналы с угло­вой модуляцией, как и при AM, могут быть представлены в виде суммы гармонических колебаний. Сравнительно просто это можно сделать для однотональной модуляции. Из (3.16) следует, что спектры ФМ и ЧМ одинаковы, если m_чм=m_ФМ=m, поэтому бу­дем рассматривать один из них, например ЧМ, полагая для упро­щения записей, что ψ₀=0 и ψ=0.

Преобразуем (3.16) по формуле косинуса суммы двух аргу­ментов

s(u_м,t)=A₀cosω₀tcos(msinΩt)- A₀sinω₀tsin(msinΩt) (3.17)

Из теории бесселевых функций известны следующие соотно­шения:

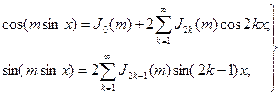(3.18)

где Jk(m) — функция Бесселя k-го порядка от аргумента m. Пос­ле подстановки (3.18) в (3.17), выполняя обычные алгебраические преобразования и раскрывая произведение тригонометрических функций, получаем

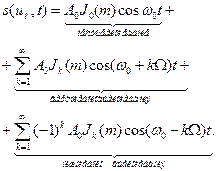(3.19)

Формулу (3.19) можно представить даже в более компактном виде, учитывая, что (-1)^kJ_k(m)=J_k(m):

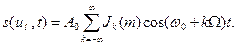
Таким образом, спектр даже для однотональной угловой модуля­ции является сложным. В (3.19) первый член — гармоническая составляющая с частотой несущей, средняя группа гармонических составляющих с частотами ω₀+kΩ является верхней боковой полосой частот, третья группа составляющих с частотами ω₀+kΩ представляет нижнюю боковую полосу частот. Число верхних и нижних боковых частот теоретически бесконечно. Боковые гармо­нические колебания расположены симметрично относительно соо на расстоянии Ω. Амплитуды всех компонент спектра, в том числе и с частотой ω_0, пропорциональны J_k(m).

Для детального анализа и построения спектральных диаграмм необходимо знание функций Бесселя J_k(m) при различных значе­ниях k иm. Их можно найти в математических справочниках. На рис. ЗЛО приведены графики функций Бесселя при k, m≤8. Зна-чения функций Бесселя, не отображенных на графиках, можно найти по рекуррентной формуле

J_k+1(m) = (2k/m)J_k(m)—J_k-1(m).

Пример 3.4. Задано аналитическое выражение модулированного сигнала

S(u_м,t)=10cos(1,256*10⁶t+3cos 6,28*10⁴t).

Построить спектральную диаграмму этого сигнала.

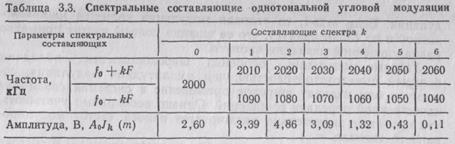
Из математического уравнения сигнала следует, что это однотональная угловая модуляция с индексом m=3. Спектральные составляющие сигнала оп­ределяем из уравнения (3.19), приняв k=0, 1, 2, 3,... (до тех пор, пока ам­плитуда составляющих будет меньше 2% Aо). Расчеты сводим в табл. 3.3, по которой и построена спектральная диаграмма (рис. 3.11).

Из графиков функций Бесселя следует интересная закономер­ность: чем больше порядок k функции Бесселя, тем при больших аргументах m наблюдается ее максимум, однако при k>m зна­чения функций Бесселя оказываются малой величиной. А раз так, то малыми будут и составляющие спектра и ими можно пренеб­речь.

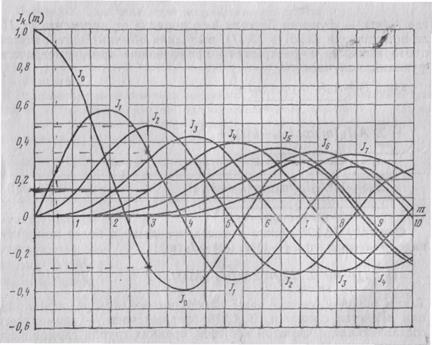
Рис. 3.10. Графики функций Бесселя

Сколько же надо взять составляющих спектра угловых моду­ляций? Все зависит от того, составляющие с какими значениями амплитуд отбрасываем. В практике считают, что можно пренеб­речь всеми спектральными составляющими, номера которых k> >m+1 (уровень меньше 5% от уровня несущей). Отсюда следу­ет, что ширина спектра сигналов с угловой модуляцией

Δf_ЧМ.ФМ.≈2(m+1)F_м, (3.20)

где F_м - - частота модулирующего сигнала. Для передачи моду­лированного сигнала с высокой точностью иногда считают, что надо учитывать спектральные составляющие с уровнем не менее 1 % от уровня несущей. Тогда ширина спектра с угловой модуля­цией

Δf_ЧМ.ФМ.≈2(m+m^1/2+1)F_м.

Если m<0,6, то угловая модуляция считается узкополосной и ее ширина спектра соизмерима с шириной спектра амплитудной модуляции. Если m>>1, то угловая модуляция является широкопо­лосной и из (3.20) следует, что ее ширина полосы частот примерно равна удвоенной девиации частоты.

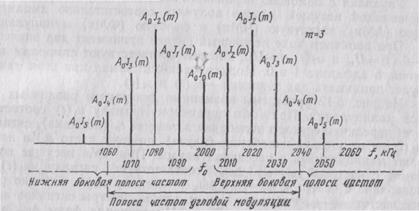
Рис. 3.11. Спектральная диаграмма сигналов с однотональной угловой модуляцией при m=3

Угловые модуляции, особенно широкополосные, обладают большей помехоустойчивостью, чем амплитудная модуляция, по­этому и они находят широкое применение в системах связи для качественной передачи сообщений. Однако необходимо учитывать, что при этом значительно расширяется полоса частот модулиро­ванного сигнала.

Если модулирующий сигнал u_m(t) является сложным и состоит из ряда гармонических составляющих, то спектр ЧМ и ФМ можно найти описанным выше методом, раскрывая выражение для коси­нуса нескольких аргументов. Однако спектр модулированного ко­лебания при этом оказывается весьма сложным, содержащим раз­личные комбинационные частоты, но общая полоса частот, зани­маемая модулированным сигналом, будет приблизительно равна 2(m+l)F_m, где F_m — максимальная частота спектра модулирую­щего сигнала u_m(t); индекс модуляции т определяется на этой максимальной частоте.

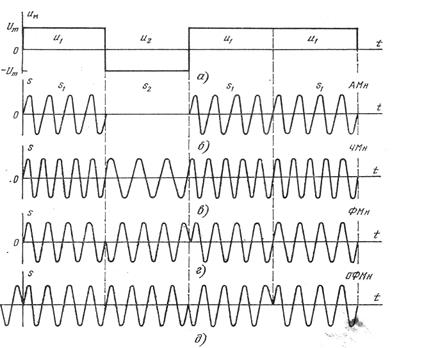
Рис. 3.12. Временные диаграммы сигналов при дискретной модуляции: а – модулирующий первичный сигнал; б – амплитудная манипуляция;

в - частотная манипуляция; г – фазовая манипуляция; д – относительная фазовая манипуляция.

положными. В связи с этим при ФМн фаза несущей меняется на 180^о при каждом переходе от u₁(t) и и₂(t) и наоборот.

В настоящее время наряду с ФМн широко применяется относительная фазовая манипуляция (ОФМн), предложенная в 1953 г. проф. Н. Т. Петровичем. Фаза несущего колебания в ОФМн изме- няется на 180^о при передаче символов 1 (сигнал u₁) и остается неизменной при передаче символов 0 (сигнал и₂)¹. Метод ОФМн предложен как способ борьбы с «обратной работой» при приеме ФМн и более подробно рассмотрен в гл. 15.

Спектр манипулированных сигналов. Сигналы s₁ (t) и s (t) — отрезки гармонических колебаний, поэтому их спектры хотя и бесконечны, но все же сосредоточены возле частот

несущих 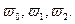Для расчета характеристик канала связи, предназначенного для передачи манипулированных сигналов, обычно не требуется знания точной структуры спектра, достаточно определить ширину спектра. Соотношения для расчета ширины

спектра двоичных манипулированных сигналов, полученные на основании формулы (2.34), сведены в табл. 3.4. Обозначения в ней следующие: В — скорость модуляции, Бод; 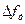— девиация частоты, Гц.

3.6. ИМПУЛЬСНАЯ МОДУЛЯЦИЯ

При импульсной модуляции несущей является периодическая последовательность импульсов одинаковой формы, обычно прямоугольных. Это последовательность характеризуется четырьмя параметрами: амплитудой Ао, длительностью t_и, частотой следования. f ₀=1 /Т и фазой импульсов (рис. 3.13, а). Все они могут бытьинформационными. Изменяя их пропорционально мгновенным значениям модулирующего сигнала и_м (t) (рис. 3.13,б), получаем четыре основные вида импульсной модуляции, а именно:

амплитудно-импульсную (АИМ) — изменяется амплитуда импульсов (рис. 3.13,в);

широтно-импульсную (ШИМ) — изменяется длительность (ширина) импульсов (рис. 3.13,г);

частотно-импульсную (ЧИМ) — изменяется частота следования импульсов (рис. 3.13,д);

фазово-импульсную (ФИМ) — импульсы сдвигаются относительно тактовых точек, за которые обычно принимают начало переднего фронта импульсов несущей (на рис. 3.13,а отмечены

кружками).

Период следования импульсов несущей определяется по теореме Котельникова (см. $2.4) Т 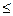(0,8...0,9) / 2F _т, где F _т — максимальная частота спектра модулирующего сигнала. Пределы изменения параметров импульсов выбираются такими, чтобы при

модуляции импульсы не перекрывались.

Спектр при импульсных видах модуляции зависит от спектра модулирующего сигнала F _и (), вида и параметров модуляции Аналитическое выражение спектра достаточно сложное. Однако примерный вид его можно получить из следующих рассуждений. Периодическую последовательность импульсов несущей можно разложить в ряд Фурье (см. пример 2.5). При модуляции каждую из гармонических составляющих ряда Фурье можно рассмат-

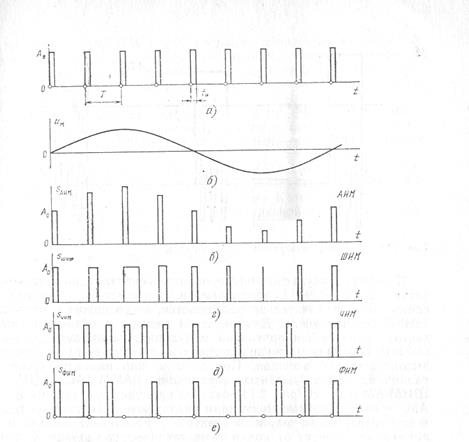
Рис. 3.13. Импульсные виды модуляции:

а – импульсная несущая; б – модулирующий сигнал; в – амплитудно-импульсная модуляция; г – широтно-импульсная модуляция; д – частотно-импульсная модуляция; е – фазо-импульсная модуляция.

ривать как индивидуальную «несущую», возле которой располагаются верхняя и нижняя боковые полосы частот. А они вычисляются по правилам, изложенным при рассмотрении модуляции гармонической несущей. Кроме того, в спектре импульсных модуляций обязательно содержится низкочастотный спектр модулирующего сигнала F _и (). При скважности S>10 боковые полосы частот не дают заметного расширения спектра в сравнении со спектром несущей.

Следовательно, для импульсных видов модуляции (кроме ШИМ) ширина спектра не зависит ни от ВША модуляции и ее параметров, ни от модулирующего сигнала, ни от периода следования импульсов, а определяется только длительностью импульса несущей и согласно (2.34) обратно пропорциональна длительности импульса несущей. Приведенные выше рассуждения справедливы и для ШИМ, но в него необходимо подставлять минимальную длительность модулированных импульсов t_{и min}, поскольку именно самый короткий импульс имеет наиболее широкий спектр.

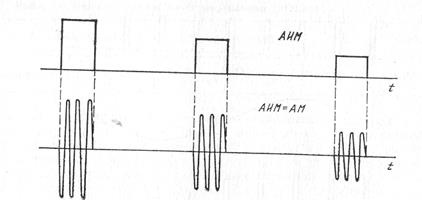
Рис. 3.14. Временные диаграммы АИМ-АМ сигнала.

Передача импульсно-модулированных сигналов по высокочастотным линиям связи принципиально невозможна, так как их спектр хотя и значительно расширяется, но содержит и низкочастотные составляющие. Для переноса спектра в область высоких

частот производится повторная модуляция, называемая двойной: модулированными импульсами снова модулируется гармоническая высокочастотная несущая. При этом можно получить более 10 различных видов двойных модуляций: АИМ-АМ, АИМ-ОМ,

ШИМ-АМ и др. На рис. 3.14 показана временная диаграмма АИМ-АМ сигнала. Двойные модуляции различаются сложностью технической реализации, шириной спектра, помехоустойчивостью, и их применение зависит от конкретных технических условий. С точки зрения помехоустойчивости предпочтительней является ФИМ-АМ

при скважности импульсов S = T/t_и 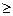10.

Пример 3.5. Для передачи речевого сигнала используется ФИМ-AN. Определить параметры импульсной модуляции и ширину спектра ФИМ-АМ.

Частота дискретизации речевого сигнала со спектром 300... 3400 Гц, по

рекомендации МККТТ, выбирается f_д =8 кГц (см. $ 2.4). Следовательно, период импульсов несущей T=l/ f_д ~=1/8 10³=1,25 10^-4 с=125 мкс. При скважности S=10 длительность импульсов несущей t_и =Т/S=125/10=12,5 мкс. Максимальное отклонение импульсов от тактовых точек при модуляции 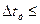(Т/2=125/2=62,5 мкс. Ширина спектра 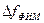=1/ t_и = 1/12,5 10^-6=8.10⁴=80 кГц.

При АМ ширина спектра удваивается, т. е. ширина спектра ФИМ-АМ будет 160 кГц.