Второй закон Кирхгофа

Алгебраическая сумма э.д.с. в любом контуре цепи равна алге­браической сумме падений напря­жения на элементах этого контура: .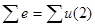

Обход контура совершается в произвольно выбранном направ­лении, например по ходу часовой стрелки. При этом соблюдается сле­дующее правило знаков для э.д.с. и падений напряжения, входящих в (2): э.д.с. и падения напряже­ния, совпадающие по направлению с направлением обхода, берутся с одинаковыми знаками.

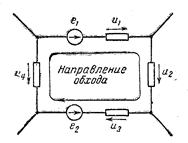Например, для данной схемы 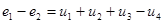.Уравнение (2) можно перепи­сать так: 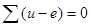. Здесь и — е — напряжение на ветви.

Следовательно, алгебраическая сумма напряжений на ветвях в лю­бом замкнутом контуре равна нулю.

Формулы (1) и (2) напи­саны в общем виде для мгновенных значений токов, напряжений и э.д.с; они справедливы для цепей как пе­ременного, так и постоянного тока.

Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.

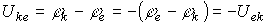(4)

Просуммируем напряжения на ветвях некоторого контура:

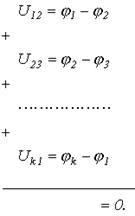
Поскольку при обходе контура потенциал каждой i -ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

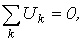(5)

- и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается 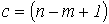независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из 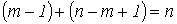уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

U=

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

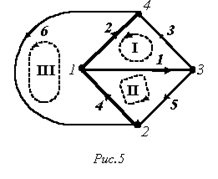В качестве примера для схемы рис. 5 имеем

,

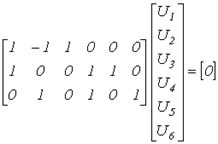откуда, например, для первого контура получаем

,

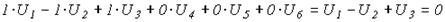что и должно иметь место.

Если ввести столбцовую матрицу узловых потенциалов

=

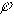причем потенциал последнего узла 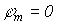, то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=AТ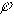

(7)

где A^Т - транспонированная узловая матрица.

Для определения матрицы В по известной матрице А = А _Д А _С, где А _Д – подматрица, соответствующая ветвям некоторого дерева, А_С - подматрица, соответствующая ветвям связи, может быть использовано соотношение В = (-А ^Т_С А ^-1Т_Д 1).