2015-06-10
826
1. Биноминальное. Пусть произведено n независимых испытаний. В каждом испытании наступает либо событие А, либо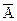 
соответственно с вероятностями р, 1 –р. Рассмотрим случайную величину x - число появлений события А в последовательности испытаний.
Закон распределения этой случайной величины можно записать следующим образом
Р (x = m) =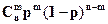 
, m=0,1,2,…n. (4)
Действительно, рассмотрим выражение (p + q)n =1 , разложим двучлен (p + q)n по формуле бинома Ньютона. Получим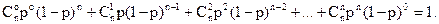 
т.е. сумма вероятностей значений случайной величины равна единице, следовательно (4) является законом распределения.
Найдем математическое ожидание:
M (x) =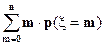 
,
Рассмотрим случайные величины x1, x2, … xn, с одинаковым законом распределения:
xk =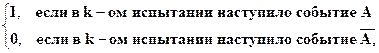 
где k = 1,2,…n. Тогда
x = x1 + x2 + … + xn.
Используя свойства математического ожидания получим:
М (x) = М (x1 + x2 + … + xn) = М (x1) + М (x2) +…+ М (xn).
Найдем математическое ожидание xk, М (xk) = 0 · (1 – p) + 1· p = р, тогда
М (x) = np
Аналогично найдем дисперсию:
D (x) = D (x1 + x2 + … + xn) = D (x1) + D (x2) +…+ D (xn)
D (xk) = (0 – p)2 (1 – p) + (1 – p)2 p = p2 (1 – p) + (1 – p)2 p =
= p (1 – p) (p + 1 – p) = p (1 – p) = p q
D (x) = n p q,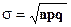 
2. Распределение Пуассона.
Пусть произведено бесконечное число испытаний. Рассмотрим случайную величину x -число появлений события А.
m = 0, 1, 2,...
Закон распределения в данном случае имеет вид:
p (x =m) =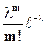 
, λ > 0 - параметр распределения, m = 0, 1, 2,... (5)
Покажем, что сумма вероятностей равна единице.
.
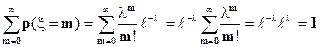Аналогично можно показать, что математическое ожидание и дисперсия соответственно равны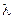 
,
М (x) = 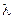, D (x) = .
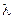Закон Пуассона называют законом редких событий.
