2015-06-10
3145
Экстремальные условия работы элементов современных конструкций, сложность их формы и большие габариты делают исключительно трудным и дорогим осуществление натурного или полунатурного эксперимента, особенно если речь идет об установлении предельных (разрушающих) нагрузок. Создание конструкций такого типа невозможно без совершенствования и автоматизации процесса проектирования, применения новых материалов и технологий.
Необходимость внедрения в производство сложнейшей техники в короткие сроки приводит к созданию систем автоматизированного проектирования. Важную роль в этих системах играет расчет на прочность.
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот.
Для многих материалов при нагружении до определенных пределов опыты показывают следующую зависимость между относительным удлинением стержня ε и напряжением σ:
ε = σ/ E, (1.1)
где ε = Δ l / l = (l 1-l)/ l – относительное удлинение стержня; Δ l – абсолютное удлинение стержня; l – длина образца до деформации; l 1 – то же, после деформации;
|
|
|
E – коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упругости первого рода.
Зависимость (2.1) носит название закон Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
Модуль упругости E характеризует жесткость материала, т.е. его способности сопротивляться деформациям.
Имея в виду, что для стержня постоянного сечения ε = Δ l / l, а σ = N / A, из формулы (2.1) можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня
Δ l = Nl /(EA). (2.2)
Между продольной ε и поперечной ε* деформациями существует установленная экспериментально зависимость
ε* = –ν ε. (2.3)
Здесь ν – коэффициент поперечной деформации (коэффициент Пуассона), характеризующий способность материала к поперечным деформациям. Для стали при упругих деформациях можно принимать значение ν приблизительно равным 0,3.
В таблице 1.1 приведены значения E иν для некоторых материалов.
Таблица 1.1 – Модуль упругости и коэффициент Пуассона для некоторых материалов
| Материал | Модуль упругости E | Коэффициент Пуассона ν |
| Сталь углеродистая | (2,0...2,1) •105 | 0,24...0,28 |
| Бронза фосфористая катана | 1,15 • 105 | 0,32...0,35 |
| Латунь холоднотянутая | (0,91...0,99) • 105 | 0,32...0,42 |
| Алюминий катанный | 0,69 • 105 | 0,32...0,36 |
| Свинец | 0,17 • 105 | 0,42 |
| Каучук | 0,00008 • 105 | 0,47 |
| Бакелит | (2...3) • 103 | 0,36 |
| Целлулоид | (14,3...27,5) • 102 | 0,33...0,38 |
| Цинк катанный | 0,84 • 105 | 0,27 |
| Никель |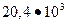 
| 0,28 |
При решении прочностных задач широко применяется метод конечных элементов (МКЭ).
|
|
|
Основная идея МКЭ состоит в том, что любую непрерывную величину (перемещение, температура, давление и т.д.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента.
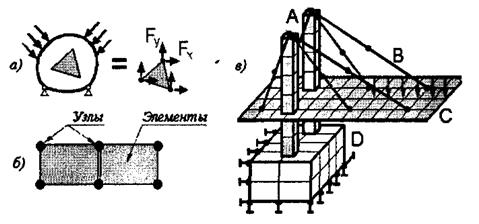
Рисунок 1.1 – Модель, разбитая на сетку конечных элементов
Решение задач с применением МКЭ состоит из следующих этапов:
1. Идентификация задачи, присвоения ей имени, создание чертежа конструкции и нагрузок.
2. Создание геометрии модели, пригодной для МКЭ.
3. Разбиение модели на сетку конечных элементов.
4. Приложение к модели граничных условий (закрепление на границе или граничные нагрузки).
5. Численное решение системы уравнений;
6. Анализ результатов.
Этапы 1, 2, 3, 4 относятся к препроцессорной стадии, этап 5 – к процессорной стадии, этап 6 – к постпроцессорной стадии.
Поясним основные понятия МКЭ на простейшем примере осевого растяжения ступенчатого стержня.
| 
|
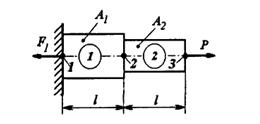
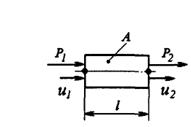
| Рисунок 1.2 – Эскиз стержня | Рисунок 1.3 – Стержневой элемент |
Ступенчатый стержень (рисунок 1.2) с двумя степенями одинаковой длины l и площадью поперечного сечения ступеней A 1 и A 2 жестко заделан с левого торца и нагружен на противоположном торце осевым усилием P. Необходимо определить перемещения сечений 1, 2 и 3.
Разобьем стержень на 2 элемента (участка) 1, 2 и введем на границах элементов узлы 1, 2, 3, в которых будем отыскивать неизвестные перемещения u. Таким образом, ступенчатый стержень будем моделировать двумя последовательно соединенными стержневыми конечными элементами. Рассмотрим отдельно стержневой элемент, изображенный на рисунке 2.3. Он имеет длину l, площадь поперечного сечения A, в узлах приложены усилия P 1 и P 2, от которых эти узлы имеют осевые перемещения u 1 и u 2. Запишем для элемента на рисунке 2.3 соотношения, очевидные из курса сопротивления материалов:
, 
,
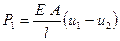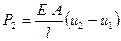Или то же в матричной форме:
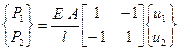, или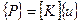 
, (2.4)
где E – модуль упругости материала стержня.
Матрица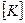 
, связывающая между собой в (2.4) узловые усилия и перемещения, носит название матрицы жесткости элемента.
Составим уравнение равновесия для всего стержня, изображенного на рисунке 2.2, объединив соотношения для элементов 1 и 2, записанные с учетом (2.4). Так как стержень состоит из нескольких элементов, то естественно предположить, что матрица жесткости всего стержня должна включать в себя матрицы жесткости образующих его элементов. Как будет показано ниже, для данной задачи главные диагонали матриц жесткости элементов должны совпадать с главной диагональю глобальной (общей) матрицы жесткости всего стержня и состыковываться в узле 2 (см. рисунок 2.2).
На основании (2.4) общую систему уравнений равновесия можно записать в виде:
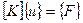
или
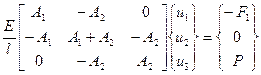. (2.5)
где ui – перемещение i -го узла всей системы. В (2.5) учтено, что усилие P приложено в узле 3, а усилие F 1 (реакция опоры) – в узле 1. Узел 2 свободен от внешних нагрузок.
Теперь следует наложить граничные условия в перемещениях, а именно: u 1 = 0. Это достигается замещением первой строки и первого столбца нулями и помещением на главную диагональ любого числа, отличного от нуля:
.
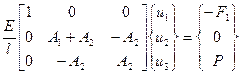Решением этой системы линейных алгебраических уравнений является:
; 
; 
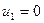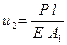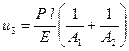. (2.6)
Исходные данные:
1. Сила Р,Н=1000;
2. Длина элементов l,м=0,5;
3. Модуль упругости первого рода Е,Па=2е11;
4. Ширина сечения а,м=0,1;
5. Ширина сечения b,м=0,1.
Результаты расчета по формуле (2.6):
; ; .
.
.
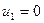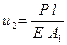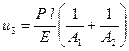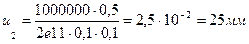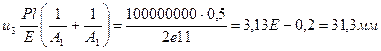Решения подобных задач проводится автоматизировано с использованием средств вычислительной техники и специализированного CAE программного обеспечения.
|
|
|
Следующим этапом лабораторной работы будет ознакомление с подобным программным обеспечением, признанным лидером в области CAE-анализа – ANSYS, а так же проведение расчета на прочность ступенчатого стержня.
ANSYS – программное обеспечение, позволяющее решать следующие задачи:
1. Построение модели конструкции (геометрия, реологические свойства, краевые условия) или импорт их из CAD-систем.
2. Изучение реакции конструкции на различные физические воздействия, такие, как воздействие различных нагрузок, температурных и электромагнитных полей, решение задач механики жидкости и газа.
3. Оптимизация геометрии конструкции.
Программная оболочка ANSYS состоит из нескольких меню (см. рисунок 2.4):
1. ANSYS Main Menu – главное меню ANSYS, служит для доступа ко всем операциям процессоров – препроцессора, процессора решения и постпроцессора.
2. ANSYS Utility Menu – меню утилит, служащее для доступа к командам, доступным из любого процессора. Это операции с файлами, управления выводом данных и другие.
3. ANSYS Toolbar – панель инструментов. Служит для быстрого доступа к ряду команд, а также для размещения кнопок доступа к макросам, написанным пользователем.
4. ANSYS Input – командное окно, служащее для ввода команд.
5. ANSYS Graphics – графическое окно, служащее для графического вывода объектов.
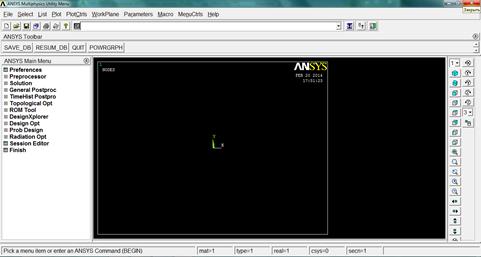
Рисунок 2.4 – Окно программы ANSYS
Далее необходимо выполнить задачу растяжения осевого стержня в программе ANSYS.
