Интегральная форма закона сохранения энергии(первый закон термодинамики)

Изменение энергии в системе вызывается разностью прихода и расхода энергии. Учитывая, что энергия может передаваться в форме теплоты и работы можно записать:

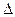E¢ = (Q¢_Tпр - Q¢_Tрасх) + (A¢_пр - A¢_расх)

Или

dE¢ = dQ¢- dA ¢ (2.44)

E¢ - штрих означает, что E отнесена к еденице массы.

dА¢ = (А¢_пр - А¢_расх) работа совершаемая над системой, поэтому перед dА¢ в уравнение (2.44) знак «–».

Энергия системы складывается из внутренней U, кинетической Eк и потенциальной Еп. Если потенциальная энергия обусловлена полем силы тяжести, то Е¢_п = gh:

Е¢ = U¢ + W²/2 + gh (2.45)

Работа может совершаться движущейся средой по преодолению внешнего давления и трения:

dА¢ = d(P/r) + dA¢_тр (2.46)

Тогда с учетом (2.45) и (2.46) уравнение (2.44) можно переписать:

dQ¢_T = dE¢ + dA¢ = dU¢ + d(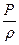) + + 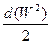gdh + dA¢_тр (2.47)

Рассмотрим частный случай закона сохранения энергии. Для изотермической идеальной жидкости (трение отсутствует, теплообмена с окружающей средой тоже нет) можно записать:

dU¢ = 0, dQ¢_T = 0, dA¢_тр = 0

Тогда получим:

d(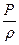) + + 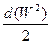gdh = 0 (2.48)

После интегрирования получим:

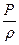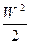+ + gh = const (2.49)

Это и есть уравнение Бернулли, выражающее закон сохранения механической энергии одиночной массы среды.

Локальная форма закона сохранения энергии.

Локальное уравнение сохранения энергии можно получить для единичного объема следующим образом:

Скорость результирующая скорость скорость Накопления = скорость совершения совершения

Энергии подвода - работы - работы

энергии против сил против сил

давления трения

Переносимая субстанция – энергия единичного объема rЕ¢. Тогда:

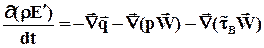(2.50)

На практике при рассмотрении процесса переноса тепла в изобарных условиях можно пренебречь работой по преодолению сил трения и изменением механической энергии, тогда можно записать:

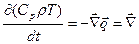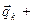
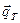( ) (2.51)

В этих условиях rE¢ = C_prT. Раскрывая выражения 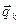и 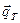получим:

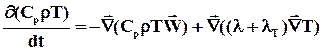(2.52)

В частном случае ламинарного движения и постоянства теплофизических характеристик (C_p, r, l = const, l_T = 0)

Это уравнение упрощается:

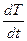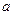= ѲT (2.53)

Здесь 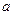= 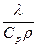- коэффициент молекулярной температуропроводности. Распишем уравнение (2.53):

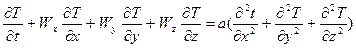– Уравнение Фурье-Кирхгофа.

При теплопереносе в неподвижной среде (W = 0) получим уравнение нестационарной теплопроводности Фурье:

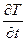= aѲT (2.54)

Для случая стационарного переноса тепла получено:

Ñ²Т = 0 (2.55)

Решение дифференциальных уравнений, полученных на основе закона сохранения совместно с условиями однозначности, позволяет получить поля температуры и поток тепла в аппарате.