Задача Коши и теорема существования и единственности решения систем дифференциальных уравнений

Рассмотрим общее решение нормальной системы.

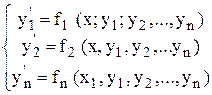. (3),

которое имеет вид:

y₁ = j₁ (x, c₁, c₂…., c_n), y₂ = j₂ (x, c₁, c₂…., c_n),…

y_n = j_n (x, c₁, c₂…., c_n),

где c₁, c₂…., c_n – произвольные постоянные.

Задаваясь начальными условиями (2), мы получаем n уравнений для определения этих произвольных постоянных.

.

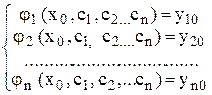Итак, задача Коши будет заключаться в том, чтобы найти решение системы (1), удовлетворяющее начальным условиям (3).

Для нормальных систем уравнений имеет место теорема, гарантирующая существование и единственность частного решения.

Теорема Коши. Если правые части нормальной системы непрерывны вместе со своими частными производными при значениях x₀, y₁₀,_… y_20,… y _n0, то существует единственная система функций y₁ (x), y₂ (x),…. y_n (x), являющаяся решением системы и удовлетворяющая заданным начальным условиям.

Таким образом, для нормальных систем дифференциальных уравнений можно сформулировать задачу и теорему Коши.