Позиционные системы счисления

Система счисления - это способ записи чисел с помощью заданного набора специальных знаков (цифр). Существуют позиционные и непозиционные системы счисления.

В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы. Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7*10² + 5*10¹ + 7*10⁰ + 7*10^-1 = 757,7

Любая позиционная система счисления характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число – два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.

В повседневной жизни предпочитают десятичную систему, потому, что с древних времен люди считали по пальцам, а пальцев у людей по десять на руках и ногах.

Кроме десятичной наиболее широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

· двоичная (используются цифры 0, 1);

· восьмеричная (используются цифры 0, 1,..., 7);

· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1,..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).

Из всех систем счисления особенно проста для технической реализации в компьютерах двоичная система счисления. Она имеет ряд преимуществ перед другими системами:

· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен - не намагничен и т.п.), а не, например, с десятью, – как в десятичной системе;

· -представление информации посредством только двух состояний надежно и помехоустойчиво;

· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

· двоичная арифметика намного проще десятичной.

Недостаток двоичной системы - быстрый рост числа разрядов, необходимых для записи чисел. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы. Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

При решении задач на позиционные системы счисления необходимо достаточно свободно владеть алгоритмами перевода в системы, наиболее важные для компьютерной техники, а именно: двоичная, восьмеричная, десятичная и шестнадцатеричная. Также необходимо умение выполнять действия сложения и вычитания в данных системах, а также корректно использовать сочетания данных алгоритмов при решении конкретных задач на системы счисления.

Любое натуральное число N может быть единственным образом представлено в системе счисления с основанием р.

N = a_n pⁿ + a_n-1 p^n-1+... + a₀ p⁰,

где a_i – цифры системы счисления; 0≤ a_i £ p-1; a_n ¹ 0;

n – число целых разрядов.

Переводы из всех позиционных систем счисления в 10-тичную систему выполняются на основе универсального определения позиционной системы счисления и заключаются в сложении степеней основания исходной системы, умноженных на коэффициенты.

Правило перевода целого числа из любой Р – ичной системы счисления в 10 – ую.

1. Запишем число в виде суммы слагаемых, где каждое слагаемое есть произведение одной из цифр переводимого числа на основание системы счисления в соответствующей степени.

2. Степень определяется следующим образом: выпишем над цифрами переводимого числа справа налево их порядковые номера, начиная с 0 (это и будет степень, в которую надо возводить основание).

Примеры:

1). Р = 8, а_i = {0, 1, 2, 3,4, 5, 6, 7}

2 1 0

613₈ = 6*8² + 1*8¹ + 3*8⁰ = 395₁₀

2). Р = 16, а_i = {0, 1, 2, 3,4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

2 1 0

18В₁₆ = 1*16² + 8*16¹ + 11*16⁰ = 395₁₀

3). Р = 2, а_i = {0, 1}

8 7 6 5 4 3 2 1 0

110001011₂ = 1*2⁸ + 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 1*2¹ + 1*2⁰ =

= 2⁸ + 2⁷ + 2³ + 2¹ + 2⁰ = 395₁₀

Перевод из 10-тичной системы в любую другую основан на алгоритме целочисленного деления числа на основание требуемой системы счисления, получаемые при этом остатки являются цифрами искомого числа.

Правило перевода целого числа из 10 – ой системы счисления в систему счисления с основанием Р (метод деления уголком)

1. Для перевода целого десятичного числа N в систему счисления с основанием р необходимо N разделить с остатком ("нацело") на основание системы счисления р (все деления выполняются в 10-тичной системе).

2. Полученный остаток будет младшей цифрой числа в новой системе (если остаток больше или равен 10, его надо заменить соответствующей цифрой в виде буквы).

3. Полученное от деления частное надо снова поделить с остатком на основание системы счисления, в которую осуществляем перевод. Остаток в этой операции даст вторую цифру числа, а частное послужит исходным материалом для получения аналогичным способом третьей цифры и так далее

4. Деление продолжается до тех пор, пока в частном не будет получено число, меньшее основания той системы счисления, в которую происходит перевод. Это частное будет старшей цифрой искомого числа.

5. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной р -ичной цифрой и записанных в порядке, обратном выполнению операций деления.

6. Если перевод осуществлялся в систему с основанием, большим 10, получившиеся двузначные остатки следует заменить соответствующими буквенными эквивалентами.

Примеры:

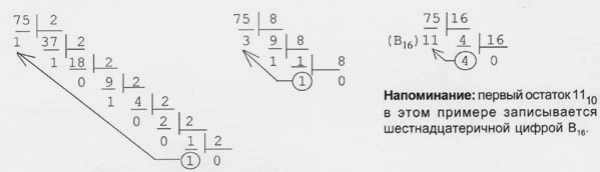
1) 395₁₀ = Х₁₆?

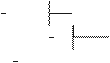395 16

32 24 16

75 16 1

64 8

11 (11₁₀ = В₁₆) Ответ: 395₁₀ = 18В₁₆

2) 395₁₀ = Х₈?

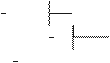395 8

32 49 16

75 48 6

72 1

3 Ответ: 395₁₀ = 613₈

3) 395₁₀ = Х₂?

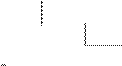
395 2

2 197 2

19 18 98 2 Ответ: 395₁₀ = 110001011₂

18 17 8 49 2

15 16 18 48 24 2

14 1 18 1 24 12 2

1 0 0 126 2

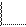0 0 3 2

1 1

При переводе числа N из 10-тичной системы в 2-ную можно воспользоваться таблицей степеней числа 2 вместо утомительного деления.

212	211	210	29	28	27	26	25	24	23	22	21	20

Правило следующее: ищется ближайшая степень числа 2, не превосходящая N. Обозначим её через «х». В этой позиции будет старшая значащая цифра двоичного числа – «1». Из числа N вычесть 2^Х. Для полученного числа опять ищется ближайшая степень числа 2, не превосходящая полученной разности. В данной позиции также будет стоять «1» и т.д. Все остальные позиции заполняются «0».

Пример: 3186₁₀ = Х₂

212	211	210	29	28	27	26	25	24	23	22	21	20

1) 2¹¹ = 2048 < 3186. В 11 позиции «1».

2) 3186 – 2048 = 1138.

3) 2¹⁰ = 1024 < 1138. В 10 позиции «1».

4) 1138 – 1024 = 114.

5) 2⁶ = 64 < 114. В 6 позиции «1».

6) 114 – 64 = 50.

7) 2⁵ = 32 < 50. В 5 позиции «1».

8) 50 – 32 = 18.

9) 2⁴ = 16 < 18. В 4 позиции «1».

10) 18 – 16 = 1. В 1 позиции «1».

11) Все остальные позиции заполняются «0».

Ответ: 3186₁₀ = 110001110010₂.