1. Прежде всего отметим, что эти алгебры равномощны и обе содержат по 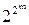 элементов т.к. если
элементов т.к. если 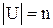 , то
, то 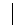 B
B 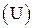
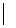 =
= 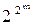 , и т.к. все двоичные функции
, и т.к. все двоичные функции 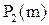 с m переменным определяются вектор-столбцом с
с m переменным определяются вектор-столбцом с 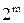 компонентами, то таких различных двоичных векторов будет
компонентами, то таких различных двоичных векторов будет 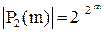 ;
;
2. Поскольку все множества U одинаковой мощности порождают изоморфные булевы алгебры (B 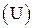 ,
, 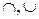
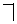 ) множеств, то эту теорему достаточно доказать для какого-либо конкретного U, удовлетворяющего условию
) множеств, то эту теорему достаточно доказать для какого-либо конкретного U, удовлетворяющего условию 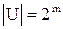 . В качестве такого множества U
. В качестве такого множества U 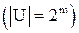 возьмем множество
возьмем множество 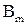 – двоичных векторов длины m и, следовательно, будем доказывать изоморфизм между булевой алгеброй множеств (B
– двоичных векторов длины m и, следовательно, будем доказывать изоморфизм между булевой алгеброй множеств (B 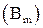 ,
, 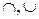
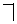 ) и булевой алгеброй функций
) и булевой алгеброй функций 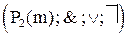 ;
;
3. Обозначим через 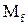 множество единичных наборов функции f. Тогда набор
множество единичных наборов функции f. Тогда набор 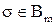 принадлежит
принадлежит 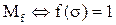 . Соответственно
. Соответственно 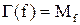 (гомоморфизм отображает f в множество единичных наборов
(гомоморфизм отображает f в множество единичных наборов 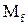 ) – между функциями и их единичными множествами является взаимно однозначным соответствием между
) – между функциями и их единичными множествами является взаимно однозначным соответствием между 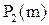 и B
и B 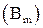 , поскольку различным функциям соответствуют различные множества, и наоборот.
, поскольку различным функциям соответствуют различные множества, и наоборот.
Определение: Функцию f, единичным множеством которой служит М, называют характеристической функцией множества М.
4. Покажем, что взаимно однозначное соответствие Г является изоморфизмом. Достаточно проверить выполнение равенств гомоморфизма для всех трех пар операций, которое в данном случае сводится к трем уравнениям:
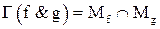
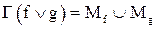
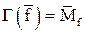 ,
,
для любых функций f и g от m переменных. Докажем втрое из них.
Пусть 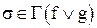 (
(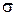 - двоичный вектор,
- двоичный вектор, 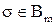 , f – единичное множество функции
, f – единичное множество функции 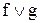 ), тогда
), тогда 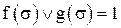 и, следовательно,
и, следовательно, 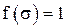 или
или 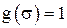 и, значит,
и, значит, 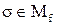 или
или 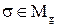 , следовательно,
, следовательно, 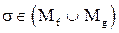 .
.
Обратно:
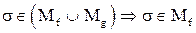 или
или 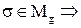
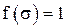 или
или 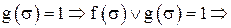
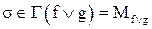 .
.
Аналогично доказываем остальные свойства.
Замечание: Во избежание путаницы обращаем внимание на различие объектов в доказанных нами теоремах.
1. В теореме 1 фигурировала алгебра со следующим основным множеством:
- 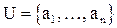 - множество произвольной природы и любой конечной мощности n;
- множество произвольной природы и любой конечной мощности n;
- B 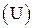 - множество подмножеств U мощности
- множество подмножеств U мощности 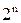 ;
;
- 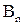 - множество двоичных векторов длины n также мощности
- множество двоичных векторов длины n также мощности 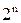 .
.
В теореме 2 участвовали:
- тот же множество 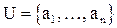 , но с дополнительным условием
, но с дополнительным условием 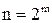 (m – любое натуральное число);
(m – любое натуральное число);
- 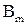 - конкретное множество U с этими же условиями:
- конкретное множество U с этими же условиями: 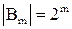 ;
;
- множество 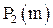 логических функций m переменных:
логических функций m переменных: 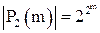 ;
;
- B 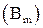 - множество подмножеств
- множество подмножеств 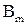 :
: 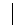 B
B 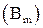
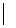 =
= 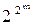 .
.
2. Множества 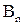 и
и 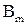 , хотя и имеют одну и ту же природу (состоят из двоичных наборов), использовались в теореме 1 и теореме 2 по-разному. В теореме 1 была использована структура элементов
, хотя и имеют одну и ту же природу (состоят из двоичных наборов), использовались в теореме 1 и теореме 2 по-разному. В теореме 1 была использована структура элементов 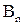 , благодаря чему над ними оказались возможными поразрядные логические операции. Подмножества
, благодаря чему над ними оказались возможными поразрядные логические операции. Подмножества 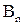 не рассматривались. В теореме 2 структура элементов
не рассматривались. В теореме 2 структура элементов 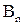 не учитывалась, само
не учитывалась, само 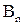
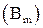 было выбрано только для естественности и наглядности, зато рассматривалась B
было выбрано только для естественности и наглядности, зато рассматривалась B 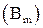 - система
- система
Таблица 1
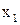
| 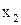
| 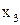
| f | g | 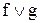
| 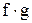
| 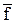
|
подмножеств 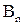 . Теоремы 1 и 2 указывают на тесную связь между множествами и логическими функциями и позволяют переходить от операций над множествами к операциям над функциями и обратно. В частности, они дают возможность непосредственно производить операции над функциями, заданными не формулами, а таблицами или единичными множествами.
. Теоремы 1 и 2 указывают на тесную связь между множествами и логическими функциями и позволяют переходить от операций над множествами к операциям над функциями и обратно. В частности, они дают возможность непосредственно производить операции над функциями, заданными не формулами, а таблицами или единичными множествами.
Из теоремы 1 и теоремы 2 следует, что булевы операции над функциями, заданными таблицами, сводятся к поразрядным логическим операциям над столбцами значений функций. Пример, приведенный в таблице, содержащей две функции f и g, и результат булевых операций над ними.
ЛИТЕРАТУРА
1. Кузнецов О. П., Адельсон - Вельский Г. М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1986. - 480 с.
2. Кук Д., Бейз Г. Компьютерная математика: Пер. с англ. - М.: Наука, Гл. ред. физ. - мат. лит., 1990. - 384 с.
3. Москинова Г. И. Дискретная математика в примерах и упражнениях. В 2-х ч. - Кемерово, Изд-во КГУ, 1993.
4.Виленкин Н. Я. Комбинаторика. - М.: Наука, гл. ред. физ.-мат. лит.,1969. – 328 с.
5. Яблонский С. В. Введение в дискретную математику/Учеб. пособие. М.: Наука, 1986. - 384 с.
6. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по курсу дискретной математики/Учеб. пособие. - М.: Наука, 1992. - 408 с.
 2015-06-28
2015-06-28 196
196






