Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сереном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
Для того чтобы написать разностную схему, приближенно описывающую данное дифференциальное уравнение, нужно:
заменить область непрерывного изменения аргумента областью дискретного его изменения,
заменить дифференциальный оператор некоторым разностным оператором, а также сформулировать разностный аналог для краевых условий и для начальных данных.
Заменим область Ω изменения аргумента x сеткой ωh, т.е. конечным множеством точек xi. Вместо функции u(x) непрерывного аргумента x ∈ Ω будем рассматривать сеточные функции y(xi), которую можно представить в виде вектора. Если пронумеровать все узлы в некотором порядке x1,x2,...,xN, то значения сеточной функции в этих узлах можно рассматривать как компоненты вектора
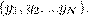
Дифференциальный оператор L, заданный в классе функций непрерывного аргумента, может быть приближенно заменен (аппроксимирован) разностным оператором Lh, заданным на сеточных функциях. Для этого каждая из производных заменяется разностным отношением, содержащим значения сеточной функции в нескольких узлах сетки. Рассмотрим пример аппроксимации первых и вторых производных функции одного переменного.
Пусть wh = {xi = ih} – сетка с шагом h на отрезке 0 ≤ x ≤ 1. Рассмотрим производную Lv = v′ функции v(x). Заменить ее разностным выражением можно бесчисленным множеством способов. Простейшими являются замены
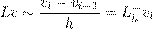 | (2.1) |
– левая разностная производная или левое разностное отношение,
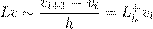 | (2.2) |
– правая разностная производная и
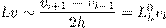 | (2.3) |
– центральная разностная производная.
При замене Lv = v′ разностным выражением Lh�vi допускается погрешность Lh�vi - 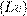 i = ψih, называемая погрешностью аппроксимации оператора L разностным оператором Lh. Естественно требовать, чтобы при стремлении h к нулю эта погрешность стремилась к нулю. Разложим v(x) по формуле Тейлора в окрестности точки x = xi
i = ψih, называемая погрешностью аппроксимации оператора L разностным оператором Lh. Естественно требовать, чтобы при стремлении h к нулю эта погрешность стремилась к нулю. Разложим v(x) по формуле Тейлора в окрестности точки x = xi
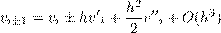
(предполагая при этом, что функция v(x) – достаточно гладкая в некоторой окрестности (x - h0,x + h0) точки x и h < h0, h0 – фиксированное число) Подставляя это разложение в (2.1)-(2.3), получим
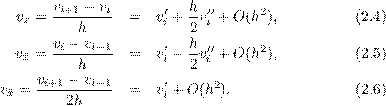
Отсюда видно, что
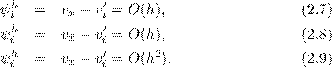
Будем говорить, что разностный оператор Lh аппроксимирует дифференциальный оператор L с порядком m > 0 в точке x, если max  h|ψih| = O(hm). Таким образом, левая и правая разностные производные аппроксимируют Lv = v′ с первым порядком, а центральная разностная производная – со вторым порядком.
h|ψih| = O(hm). Таким образом, левая и правая разностные производные аппроксимируют Lv = v′ с первым порядком, а центральная разностная производная – со вторым порядком.
Рассмотрим теперь вторую производную Lv = v′′ = 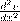 . Чтобы написать разностную аппроксимацию второй производной, надо использовать трехточечный шаблон, состоящий из узлов xi-1,xi,xi+1, в этом случае
. Чтобы написать разностную аппроксимацию второй производной, надо использовать трехточечный шаблон, состоящий из узлов xi-1,xi,xi+1, в этом случае
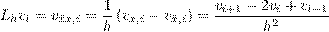 | (2.10) |
Пользуясь разложением функции v(x) по формуле Тейлора, можно показать, что порядок аппроксимации в этом случае равен двум, т.е.
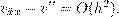
так как
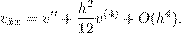 | (2.11) |
 2015-06-24
2015-06-24 944
944








