Определение. Векторным произведением двух ненулевых векторов 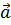 и
и 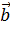 называется такой вектор
называется такой вектор 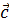 , что:
, что:
1. 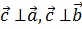 и тройка векторов
и тройка векторов 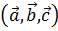 – правая
– правая  ;
;
2. 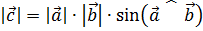 .
.
Обозначение: 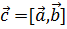 или
или 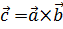 .
.
Простейшие свойства векторного умножения
1. 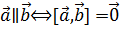 .
.
Доказательство. Если 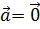 или
или 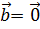 , то доказательство очевидно. Если
, то доказательство очевидно. Если 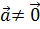 и
и 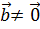 , то
, то 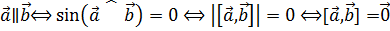 .
. 
2. Геометрический смысл векторного произведения: если из одной точки пространства построить представителей векторов 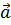 и
и 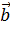 , и на этих отрезках достроить параллелограмм, то площадь параллелограмма будет равна модулю векторного произведения
, и на этих отрезках достроить параллелограмм, то площадь параллелограмма будет равна модулю векторного произведения 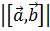 .
.
Алгебраические свойства векторного умножения
1. Антикоммутативность: 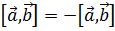 .
.
2. Ассоциативность (относительно скалярного множителя): 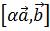 =
= 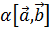
3. Дистрибутивность: 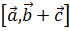 =
= 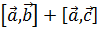 .
.
Следствие. Исходя из свойств векторного умножения, можно умножать линейную комбинацию векторов на другую линейную комбинацию некоторых векторов по правилу умножения многочленов. Но здесь важно учитывать порядок сомножителей в силу антикоммутативности векторного умножения векторов.
Пример
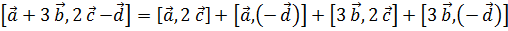 =
= 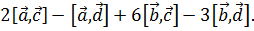
Векторное произведение в координатной форме
Пусть в репере 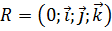 векторы имеют координаты:
векторы имеют координаты: 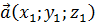 ,
, 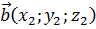 ,
, 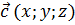 , где
, где 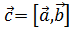 . Имеем разложение по базису:
. Имеем разложение по базису: 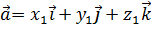 ,
, 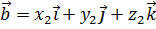 . Вектора базиса связаны соотношениями:
. Вектора базиса связаны соотношениями: 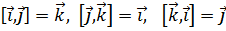 и
и 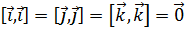 .
.
Так как 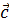 =
= 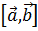 =
= 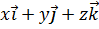 , то:
, то:
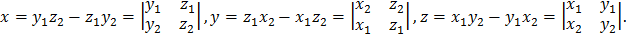
То есть, вектор 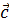 имеет координаты:
имеет координаты: 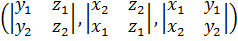 .
.
Существует такая условная запись: 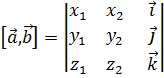 .
.
Пример. 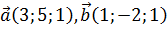 . Тогда:
. Тогда:
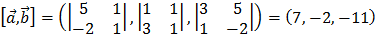 .
.
 Задача. Определите площадь треугольника
Задача. Определите площадь треугольника 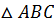 по координатам его вершин.
по координатам его вершин.
Пусть в репере R= 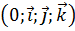 даны точки
даны точки 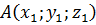 ,
, 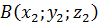 ,
, 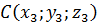 . Тогда площадь треугольника
. Тогда площадь треугольника 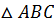 равна половине площади параллелограмма, натянутого на вектора
равна половине площади параллелограмма, натянутого на вектора 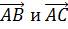 .
.
Используя геометрический смысл векторного произведения, имеем:
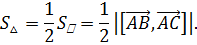
Вычисляем: 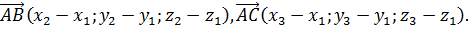 Пусть
Пусть 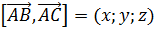 . Тогда
. Тогда
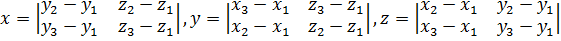 ,
,
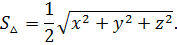
 2015-06-28
2015-06-28 1002
1002








