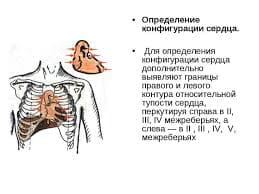
Лемма. Любая ДНФ (КНФ) имеет единственную равносильную СДНФ (СКНФ).
►Чтобы найти СДНФ по некоторой ДНФ, нужно каждое слагаемое, при необходимости, дополнить до полного числа литералов. Для этого определяется максимальное число переменных, и каждое слагаемое «умножается» на единицу из недостающих литералов. Фактически на разбиение единицы, осуществленное недостающими литералами. Единственность следует из единственности разложения единицы. ◄
Алгоритм приведения произвольной формулы к СДНФ.
6. Формула приводится к стандартному базису.
7. Операции отрицания «спускаются» на литералы с помощью законов де Моргана.
8. Раскрываются скобки и, при необходимости, удаляются повторяющиеся ЭК – в результате формула приводится к ДНФ.
9. Каждая ЭК в формуле превращается в сумму конституент. Снова, при необходимости, удаляются повторяющиеся ЭК.
Результат – любая формула, кроме нуля, представлена в виде дизъюнкции конституент, т. е. получена СДНФ.
Подсчитаем общее количество СДНФ из n переменных. Общее количество конституент N=2n, т.к. каждая из n переменных принимает два значения. Из множества из N элементов можно составить ровно 2N подмножеств, т.е. наборов-дизъюнкций различных конституент. Но из этого количества нужно вычесть единицу – нуль нельзя представить в виде СДНФ. Таким образом, полное число СДНФ совпадает с полным числом булевых функций без константы 0, и поэтому можно сделать вывод, что любая булева функция, кроме нуля, представима в виде СДНФ. Это и есть утверждение теоремы, которую мы сейчас докажем.
|
|
|
Лемма. Для любой булевой функции справедлива формула:
f(x1,x2,…,xn)=(x1)Ùf(0, x2,…,xn) Úx1Ùf(1, x2,…,xn)
►Две булевы функции равны, если они совпадают на всех наборах переменных. Для проверки формулы достаточно зафиксировать произвольный набор (x2,…,xn)=(а2,…,аn) и перебрать значения функций на двух возможных значениях аргумента х1=0,1.
Сравниваем на 0:
f(0,а2,…,аn)=(0)Ùf(0, а2,…,аn) Ú 0Ùf(1, а2,…,аn)= f(0,а2,…,аn)
Сравниваем на 1:
f(1,а2,…,аn)=(1) Ùf(0, а2,…,аn) Ú 1Ùf(1, а2,…,аn)= f(1,а2,…,аn)
Следовательно, функции в левой и правой частях равенства совпадают на всех наборах, т.е. они равны. ◄
Очевидно, что подобное разложение можно провести по любой переменной.
Далее можно продолжить процесс разложения и получить формулу разложения по произвольному набору переменных. Если провести разложение по всем переменным то, очевидно, получится СДНФ данной булевой функции.
Следствием данного рассуждения является
Теорема. Любая булева функция, не равная тождественно нулю, единственным образом представима в виде СДНФ.
Чтобы записать формулу разложения в компактном виде, введём обозначения:
|
|
|
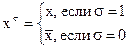 Так,
Так, 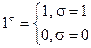 , а
, а 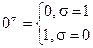
С использованием этих обозначений получаем формулу разложения:
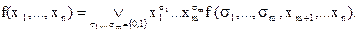
Следствием формулы разложения является представление булевой функции в виде СДНФ:
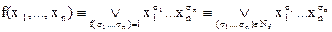
Рассмотрим еще одно доказательство данной теоремы, основанное на геометрических идеях.
Булева функция f есть отображение n-мерного булева куба Bn в одномерный булев куб B: f: Bn→B. Носитель функции Nf определяется как множество f: Nf→1, т.е. множество, на котором булева функция принимает значение 1. Каждую точку из (этого множества называют конституентой единицы, а каждую точку из дополнения – конституентой нуля. Поставим в соответствие каждой конституенте 1: (σ1, σ2,…,σn), f(σ1, σ2,…,σn)=1 элементарную конъюнкцию 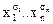 , которую тоже называют конституентой 1. Непосредственно проверяется, что эта ЭК равна единице на наборе (σ1, σ2,…,σn) и только на нем. Дизъюнкция всех таких элементарных конституент и будет СДНФ, т.к. она принимает значение 1 на тех и только тех наборах, на которых f=1. Следствием геометрического подхода является вторая равносильность в формуле.
, которую тоже называют конституентой 1. Непосредственно проверяется, что эта ЭК равна единице на наборе (σ1, σ2,…,σn) и только на нем. Дизъюнкция всех таких элементарных конституент и будет СДНФ, т.к. она принимает значение 1 на тех и только тех наборах, на которых f=1. Следствием геометрического подхода является вторая равносильность в формуле.
Пример: построим СДНФ для импликации. x→y ≡ 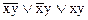
 2015-06-24
2015-06-24 1108
1108