Главные площадки и главные напряжения

Главными называются площадки, на которых касательные напряжения равны нулю. Нормальные напряжения на главных площадках называются главными напряжениями.

Обратимся к соотношению (6), описывающему преобразование вектора нормали к площадке в вектор напряжений на ней. Применим эти соотношения к главной площадке. Обозначим s главное напряжение, действующее на этой площадке (l,m,n – ее направляющие косинусы). Поскольку касательные напряжения на главной площадке отсутствуют, это напряжение s является полным напряжением S = s, его направление совпадает с нормалью, следовательно, его проекции на оси координат составляют:

S_x = s*l,

S_y = s*m,

S_z = s*n.

Подставим эти выражения в (6-а) и сгруппируем слагаемые с одинаковыми направляющими косинусами. Получим систему уравнений:

(s_x-s)·l + t_xy·m + t_zx·n = 0

t_xy·l + (s_y-s)·m + t_yz·n = 0 (10)

t_zx·l + t_yz·m + ( s_z-s)·n = 0

Направляющие косинусы l,m,n связаны соотношением:

l² + m² + n² = 1 (11)

Если задана матрица напряжений (s), то соотношения (10)+(11) составляют систему четырех уравнений с четырьмя неизвестными, из которых можно найти величину главного напряжения s и направляющие косинусы главной площадки l,m,n. Исследуем эту систему.

Соотношения (10) составляют систему из 3-х линейных однородных уравнений относительно направляющих косинусов l,m и n. Эта система имеет очевидное нулевое решение l = m = n = 0, которое не представляет для нас интереса, поскольку не удовлетворяет уравнению (11). Известно, что система линейных уравнений, в которой число уравнений равно числу неизвестных, имеет единственное решение, если определитель, составленный из ее коэффициентов не равен нулю. Система (10) может иметь решения, удовлетворяющие уравнению (11) только в том случае, когда нулевое решение не единственно, то есть когда определитель равен нулю. Следовательно, четвертое неизвестное,т.е. главное напряжение должно удовлетворять уравнению:

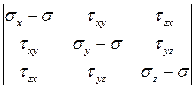= 0 (12-а)

Раскрыв определитель, получим кубическое уравнение относительно главного напряжения s:

s³ - Аs² + Вs - С = 0, (12)

где А = s_x + s_y + s_z

В = s_xs_y + s_ys_z + s_zs_x - t_xy² - t_yz² - t_zx² (13)

С = s_xs_ys_z + 2t_xyt_yzt_zx –(s_xt_yz² +s_yt_zx² +s_zt_xy²).

Уравнение (12) называется характеристическим уравнением матрицы напряжений. Три корня этого уравнения s₁, s₂, s₃ - это три главных напряжения, которые принято нумеровать в порядке убывания от максимального значения до минимального (алгебраически): s₁ ³ s₂ ³ s₃.

Каждому главному напряжению соответствует главная площадка, направляющие косинусы которой находятся из решения системы уравнений (10)-(11), если в нее вместо s подставить найденное главное значение. Главное напряжение обращает в ноль определитель системы (10), следовательно, эта система особенная, ее уравнения не являются независимыми. Поэтому одно из них следует отбросить и определять три направляющих косинуса главной площадки, решая оставшиеся два уравнения совместно с уравнением (11).

Примем без доказательства следующие положения:

- все корни характеристического уравнения вещественны для любой симметричной матрицы;

- три главные площадки взаимно перпендикулярны, их нормали образуют ортогональную систему главных осей матрицы напряжений.