Теорема 6. Поворот плоскости есть произведение двух осевых симметрий, оси которых пересекаются. Центром поворота будет точка пересечения осей, а угол поворота равен двойному углу от первой оси до второй.
Доказательство. a=2j, f = S2·S1. Необходимо показать, что движение f - поворот. Действительно f - движение первого рода (т.е. либо параллельный перенос, либо поворот,), так как ориентация репера меняется дважды и возвращается к исходному. При осевой симметрии S1 неподвижными точками будут точки прямой l1, а при осевой симметрии S2 - точки прямой l2, но точка О останется неподвижной как в первом так и во втором случаях.
Следовательно, движение f имеет одну неподвижную точку О. Следовательно, f - поворот вокруг точки О.
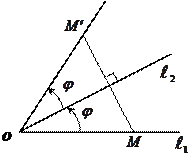 |
Найдем угол поворота: возьмем произвольно точку МÎl1 f(M)=S2(S1(M))=S2(M)=M', a=2j. f - поворот на угол 2j вокруг точки О. Докажем обратное. Пусть мы имеем поворот на угол 2j вокруг точки О (угол 2j - ориентированный). Проведем через точку О пару прямых l1 и l2 так, чтобы угол от прямой l1 к прямой l2 составлял j.

Поэтому 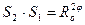 . Если бы мы взяли ещё пару прямых, проходящих через точку О, угол между которыми был бы равен j и рассмотрели бы произведение осевых симметрий
. Если бы мы взяли ещё пару прямых, проходящих через точку О, угол между которыми был бы равен j и рассмотрели бы произведение осевых симметрий 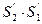 относительно этих осей, то это был бы один и тот же поворот
относительно этих осей, то это был бы один и тот же поворот
▄
Теорема 7. Параллельный перенос 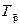 плоскости есть произведение двух осевых симметрий, оси которых
плоскости есть произведение двух осевых симметрий, оси которых  и l2 параллельны и удовлетворяют условию: 1)
и l2 параллельны и удовлетворяют условию: 1) 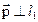 , 2) расстояние между осями равно
, 2) расстояние между осями равно 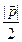 и направление вектора
и направление вектора 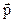 совпадает c направлением от первой прямой до второй.
совпадает c направлением от первой прямой до второй.
Доказательство. Пусть прямые  и l2 параллельны и удовлетворяют условию: 1)
и l2 параллельны и удовлетворяют условию: 1) 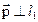 , 2) расстояние между осями равно
, 2) расстояние между осями равно 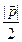 , и направление вектора
, и направление вектора 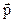 совпадает c направлением от первой прямой до второй. Обозначим осевые симметрии относительно этих прямых, соответственно,
совпадает c направлением от первой прямой до второй. Обозначим осевые симметрии относительно этих прямых, соответственно, 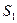 и
и 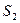 .
.
Произведение  - есть движение первого рода (т.к. не меняет ориентации). Неподвижных точек здесь нет. Поэтому, это движение является параллельным переносом. Найти вектор этого параллельного переноса можно так:
- есть движение первого рода (т.к. не меняет ориентации). Неподвижных точек здесь нет. Поэтому, это движение является параллельным переносом. Найти вектор этого параллельного переноса можно так:
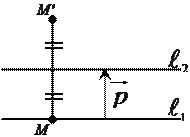 выберем точку
выберем точку  и найдем ее образ
и найдем ее образ 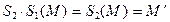 Þ
Þ 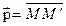 .
.
Длина вектора 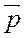 в два раза больше расстояния между данными параллельными прямыми
в два раза больше расстояния между данными параллельными прямыми  и l2, а направление вектора
и l2, а направление вектора 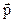 совпадает c направлением от первой прямой до второй и
совпадает c направлением от первой прямой до второй и 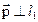 . Докажем обратное: покажем, что параллельный перенос есть произведение двух осевых симметрий с параллельными осями. Вектор
. Докажем обратное: покажем, что параллельный перенос есть произведение двух осевых симметрий с параллельными осями. Вектор 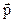 - определен. Проведем две параллельные прямые, перпендикулярные вектору
- определен. Проведем две параллельные прямые, перпендикулярные вектору 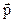 , так чтобы расстояние между ними было равно
, так чтобы расстояние между ними было равно 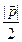 ,и направление от первой прямой до второй совпадало с вектором
,и направление от первой прямой до второй совпадало с вектором 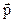 . Тогда, как доказано выше,
. Тогда, как доказано выше,
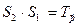 .
.
Замечание: мы можем пару параллельных прямых, определяющих параллельный перенос смещать параллельно и при этом параллельный перенос остается прежним.
▄
Теорема 8. Всякое движение плоскости можно представить в виде произведения не более трех осевых симметрий.
Доказательство. Мы имеем параллельный перенос - произведение двух осевых симметрий; поворот - произведение двух осевых симметрий; скользящая симметрия есть произведение осевой симметрии и параллельного переноса, следовательно, произведение трех осевых симметрий.
▄
Теорема 9. Если прямые 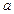 и b перпендикулярны, то
и b перпендикулярны, то
S 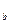 × S
× S 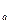 = S
= S 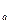 × S
× S 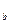 = Z0, О - точка пересечения прямых а и b.
= Z0, О - точка пересечения прямых а и b.
Доказательство. Пусть а ^ b. Если О - точка пересечения прямых а и b, то композиция S 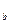 × S
× S 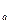 представляет собой поворот на угол 180°, то есть центральную симметрию относительно точки О: S
представляет собой поворот на угол 180°, то есть центральную симметрию относительно точки О: S 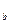 × S
× S 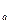 = Z0. Аналогично, композиция S
= Z0. Аналогично, композиция S 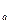 × S
× S 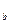 =Z0 .
=Z0 .
Следовательно, S 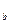 × S
× S 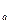 = S
= S 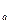 × S
× S 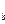 .
.
▄
Теорема 10. Если имеет место равенство S 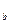 × S
× S 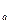 = S
= S 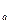 × S
× S 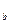 ,
,
то а ^ b.
Доказательство. Докажем методом от противного: предположим а и b не перпендикулярны, тогда они или пересекаются под углом a¹9°, или параллельны.
Если прямая а пересекается с b под углом a ¹ 9°, то S 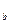 × S
× S 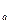 есть поворот вокруг точки пересечения прямых на угол 2a, а композиция S
есть поворот вокруг точки пересечения прямых на угол 2a, а композиция S 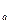 × S
× S 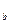 – поворот вокруг той же точки, но на угол –2a, т.е. S
– поворот вокруг той же точки, но на угол –2a, т.е. S 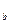 × S
× S 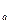 ¹ S
¹ S 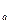 × S
× S 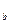 .
.
Если а || b, то S 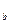 × S
× S 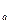 и S
и S 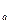 × S
× S 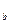 - параллельные переносы на противоположные векторы 2
- параллельные переносы на противоположные векторы 2 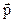 и –2
и –2 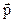 . Поэтому S
. Поэтому S 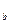 × S
× S 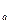 ¹ S
¹ S 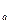 × S
× S 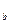 .
.
Но это противоречит условию. Следовательно, если имеет место равенство S 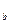 × S
× S 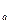 = S
= S 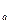 × S
× S 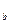 , то прямые, определяющие эти симметрии взаимно перпендикулярны.
, то прямые, определяющие эти симметрии взаимно перпендикулярны.
▄
 2015-07-04
2015-07-04 5035
5035
