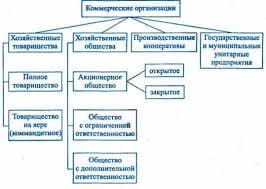
All the vital points about potential energy can be made by focusing on the example of gravitational potential energy. For simplicity, we treat only vertical motion, and motion close to the surface of the earth, where the gravitational force is nearly constant. To find an equation for gravitational  , we examine the case of free fall, in which energy is transformed between kinetic energy and gravitational
, we examine the case of free fall, in which energy is transformed between kinetic energy and gravitational  . Whatever energy is lost in one form is gained in an equal amount in the other form, so using the notation
. Whatever energy is lost in one form is gained in an equal amount in the other form, so using the notation 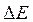 to stand for
to stand for 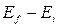 and a similar notation for
and a similar notation for 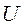 , we have
, we have
(1) 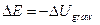 .
.
We know an equation for kinetic energy,
(2) 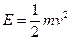
so if we can relate v to height, y, we will be able to relate 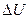 to y, which would tell us what we want to know about potential energy. The y component of the velocity can be connected to the height via the constant acceleration equation
to y, which would tell us what we want to know about potential energy. The y component of the velocity can be connected to the height via the constant acceleration equation
(3) 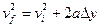
and Newton’s second law provides the acceleration,
(4) 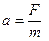
in terms of the gravitational force. The algebra is simple because both equation (2) and equation (3) have velocity to the second power. Equation (2) can be solved for 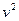 to give
to give 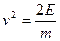 , and substituting this into equation (3), we find
, and substituting this into equation (3), we find
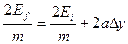 .
.
Making use of equations (1) and (4) gives the simple result
(5) 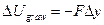 .
.
Change in gravitational 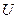 resulting from a change in height
resulting from a change in height 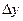 ; F is the gravitational force on the object, i.e. its weight; valid only near the surface of the earth, where F is constant.
; F is the gravitational force on the object, i.e. its weight; valid only near the surface of the earth, where F is constant.
(6) 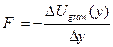
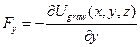

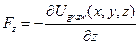
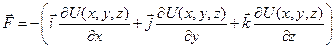
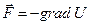
 2015-07-03
2015-07-03 391
391