Определение условного экстремума функции многих переменных путем сокращения числа переменных

Пусть необходимо найти экстремум функции Z=f(х₁, х₂, …, x_n) при условии, что переменные х₁, х₂, …, x_n удовлетворяют уравнениям:

φ_i(х₁, х₂, …, x_n) = 0, i=1,2, …,m, m<n (7.8)

Предполагается, что функции f и φ_i имеют непрерывные частные производные по всем переменным. Уравнения (7.8) называются уравнениями связи.

Говорят, что в точке Х⁰ = (х⁰₁, х⁰₂, …, x⁰_n), удовлетворяющей уравнениям связи (7.8), функция Z=f(X) имеет условный максимум(минимум), если неравенство f(X⁰) ≥ f(X) (f(X⁰)≥ f(X)) имеет место для всех точек Х, координаты которых удовлетворяют уравнениям связи.

Легко заметить, что задача определения условного экстремума совпадает с задачей нелинейного программирования (7.3)-(7.4).

Один из способов определения условного экстремума на границах области D применяется в том случае, если из уравнений связи (7.8) m переменных, например, х₁, х₂, …, x_m, можно явно выразить через оставшиеся n-m переменных:

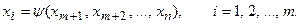(7.9)

Подставив полученные выражения для x_i в функцию Z, получим

Z = f(ψ₁(x_m+1, …, x_n), …, ψ_m(x_m+1, …, x_n), x_m+1, …, x_n),

или Z = F(x_m+1, …, x_n). (7.10)

Таким образом, задача свелась к нахождению локального (глобального) экстремума для функции (7.10) от n-m переменных.

Доказано, что если в точке 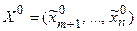функция (7.10) имеет экстремум, то в точке 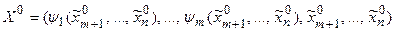функция

Z=f(x₁, …, x_n) имеет условный экстремум (сформулированный выше).