Заняття 19
Эмпирические зависимости. В научных и инженерных исследованиях часто возникает задача математического описания некоторого исследуемого процесса или объекта. Для определенности предположим, что связь независимой переменной 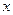 и зависимой переменной
и зависимой переменной 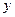 выражается в общем случае нелинейной функций
выражается в общем случае нелинейной функций 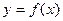 . Функция
. Функция 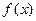 является неизвестной, но значения переменных
является неизвестной, но значения переменных 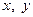 могут быть измерены и результаты таких измерений представлены таблицей
могут быть измерены и результаты таких измерений представлены таблицей 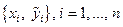 , где
, где 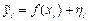 ,
, 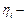 погрешности измерений, имеющие случайную природу.
погрешности измерений, имеющие случайную природу.
Задача построений эмпирической зависимости состоит в нахождении функции S(x), как можно точнее аппроксимирующей неизвестную f(x).
Решение этой задачи включает два этапа.
Этап 1. Выбор класса функций, из которого выбирается S(x). Например, S(x) выбирается из класса линейных функций вида S(x)=а0+а1х, где а0, а1 – параметры. Таким образом, на этом этапе эмпирическая зависимость выбирается с «точностью» до её параметров. Выбор класса функций осуществляется на основе анализа диаграммы рассеяния (в декартовой системе координат наносятся точки 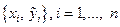 ) или на основе достоверной априорной информации. Например, из курса физики известно, что сопротивление металлического проводника линейно зависит от его температуры.
) или на основе достоверной априорной информации. Например, из курса физики известно, что сопротивление металлического проводника линейно зависит от его температуры.
Этап 2. Вычисление неизвестных параметров функции S(x) с использованием таблицы измерений. Параметры вычисляются из условия минимума некоторого функционала F(a). Наиболее часто в качестве такого функционала используется функционал метода наименьших квадратов, имеющий вид:
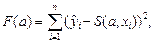 (1.1)
(1.1)
где запись S(а, x) указывает на наличие у функции S(x) параметров {aj}, j=1, 2,…, M.
Функции MathCAD для построения эмпирических зависимостей. В пакет MathCAD включены функции для вычисления параметров различных функций S(x). Обращения к этим функциям приведены в табл. 1.1, где Х – вектор, составленный из значений { xi }, i= 1, …, n, а Y – вектор, сформированный из значений 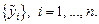
Таблица 1.1
| Функция | Назначение функции |
| slope(x, y) | Вычисляет параметр а1 линейной функции 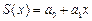 |
| intercept(x, y) | Вычисляет параметр а0 линейной функции 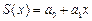 |
| regress(x,y,m) | Вычисляет параметры 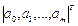 полиномиальной функции полиномиальной функции 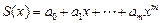 для любого m (на практике для любого m (на практике 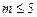 ). Вычисленные параметры размещаются в результирующем векторе, начиная с четвертой проекции (см. пример 1.2) ). Вычисленные параметры размещаются в результирующем векторе, начиная с четвертой проекции (см. пример 1.2) |
| line(x, y) | Вычисляет параметры а0, а1 линейной зависимости 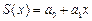  |
| linfit (x, y,Ф) | Вычисляет параметры 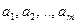 линейной комбинации линейной комбинации 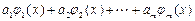 Базисные функции Базисные функции 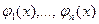 являются проекциями вектора-функции Ф(x), формируемого до обращения к функции linfit являются проекциями вектора-функции Ф(x), формируемого до обращения к функции linfit |
| genfit(x,y,ао,F) | Вычисляет параметры 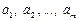 нелинейной функции S(x). До обращения формируется F(x,a) – вектор-функция размерности (m+1), составленный из самой функции S(x) и частных производных нелинейной функции S(x). До обращения формируется F(x,a) – вектор-функция размерности (m+1), составленный из самой функции S(x) и частных производных 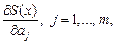 ао – вектор размерности m, составленный из «стартовых» значений параметров ао – вектор размерности m, составленный из «стартовых» значений параметров 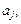 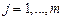 (см. пример 1.3) (см. пример 1.3) |
Замечание 1.1. Для вычисления значения эмпирической зависимости в точке 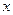 с параметрами
с параметрами 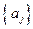 , найденными с помощью функции regress, используется функция interp(v, X, Y, x), где v – вектор, результат работы функции regress (см. пример1.2 ). Вычисление других эмпирических зависимостей осуществляется с использованием функций пользователя (см. примеры 1.1, 1.3).
, найденными с помощью функции regress, используется функция interp(v, X, Y, x), где v – вектор, результат работы функции regress (см. пример1.2 ). Вычисление других эмпирических зависимостей осуществляется с использованием функций пользователя (см. примеры 1.1, 1.3).
Замечание 1.2. Разница между функциями linfit и genfit заключается в том, что параметры а1,…, аm функции linfit находятся из решения линейной системы уравнений, а в функции genfit из нелинейной системы, и поэтому задаётся точка старта (вектор ао) итерационной процедуры построения решения этой нелинейной системы.
Пример 1.1. Значения линейной зависимости 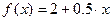 измерялись в
измерялись в 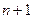 узлах
узлах 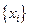 с относительным уровнем шума
с относительным уровнем шума 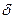 . Построение линейной эмпирической зависимости показано на рис. 1.1. ¨
. Построение линейной эмпирической зависимости показано на рис. 1.1. ¨
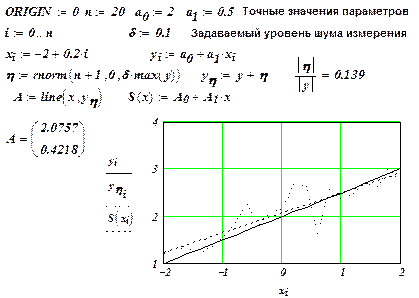
Рис. 1.1. Построение линейной эмпирической зависимости
Пример 1.2. По исходным данным, приведенным на рис. 1.2, построить полиномиальные эмпирические зависимости вида 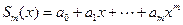 при m = 2 и m = 3. Построение этих эмпирических зависимостей показано в документе, приведенном на рис. 1.2. Видно, что при m = 3 эмпирическая зависимость в большей степени адекватна исходным экспериментальным данным, т.е. более близко подходит к измеренным значениям
при m = 2 и m = 3. Построение этих эмпирических зависимостей показано в документе, приведенном на рис. 1.2. Видно, что при m = 3 эмпирическая зависимость в большей степени адекватна исходным экспериментальным данным, т.е. более близко подходит к измеренным значениям 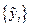 . ¨
. ¨
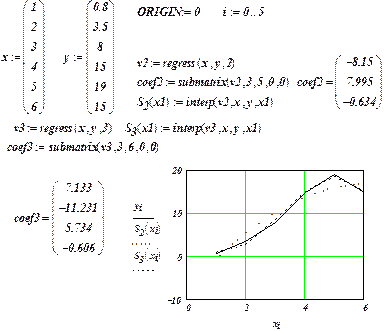
Рис. 1.2. Построение полиномиальных зависимостей
Пример 1.3. По данным, приведенным на рис. 1.3 (векторы 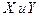 ), построить эмпирическую зависимость вида
), построить эмпирическую зависимость вида
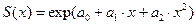 .
.
Построение выполнено в документе MathCAD, показанном на рис. 1.3, с использованием функции genfit. Перед обращением к этой функции формируется вектор-функция 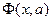 , первая проек проекция которого содержит формулу эмпирической зависимости, а три других проекции частные производные от этой формулы по параметрам
, первая проек проекция которого содержит формулу эмпирической зависимости, а три других проекции частные производные от этой формулы по параметрам 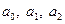 соответственно. Окружностями отмечены измеренные значения
соответственно. Окружностями отмечены измеренные значения 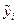 . ¨
. ¨
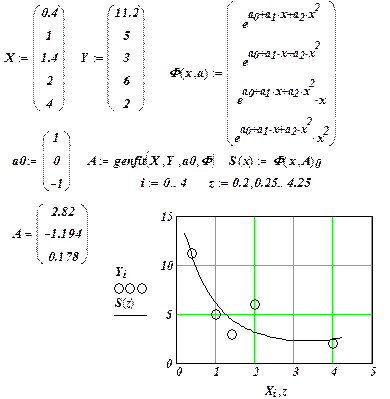
Рис. 1.3. Построение нелинейной зависимости
Кроме функций вычислений параметров «универсальных» эмпирических зависимостей, приведенных в табл. 1.1, определены функции, вычисляющие параметры «специальных» эмпирических зависимостей. В табл. 1.2 приведено обращение к этим функциям.
Таблица 1.2
| Функция | Назначение функции |
| expfit(X,Y,ao) | Вычисляет параметры а1, а2, а3 экспоненциальной зависимости 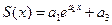 . Вектор ао (размерности 3) определяет точку старта, т.е. задает «начальное» значение для а1, а2, а3 . Вектор ао (размерности 3) определяет точку старта, т.е. задает «начальное» значение для а1, а2, а3 |
| lgsfit(X,Y,ao) | Вычисляет параметры а1, а2, а3 зависимости 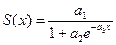 . Вектор ао (размерности 3) определяет «стартовые» значения для а1, а2, а3 . Вектор ао (размерности 3) определяет «стартовые» значения для а1, а2, а3 |
| lnfit(X,Y) | Вычисляет параметры а1, а2 зависимости 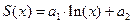 |
| logfit(X,Y, ao) | Вычисляет параметры а1, а2, а3 зависимости 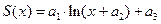 .Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 .Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 |
| pwrfit(X,Y,ao) | Вычисляет параметры степени зависимости 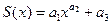 . Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 . Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 |
| sinfit(X,Y,ao) | Вычисляет параметры синусоидальной зависимости 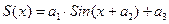 . Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 . Вектор ао (размерности 3) задаёт «стартовые» значения для а1, а2, а3 |
Пример 1.4. По данным, приведенным на рис. 1.4, построить эмпирическую зависимость вида
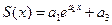 .
.
Построение этой эмпирической зависимости показано в документе MathCAD, приведенном на рис. 1.4. ¨
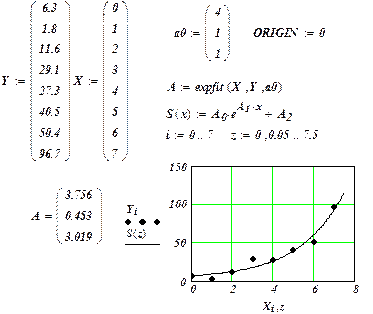
Рис. 1.4. Построение экспоненциальной зависимости
Приведенные в табл. 1.1 и 1.2 функции осуществляют построение эмпирических зависимостей, которые можно назвать «глобальными», так как при вычислении их параметров используется вся таблица исходных данных. В ряде экспериментов возникает необходимость построить эмпирическую зависимость по некоторому небольшому набору исходных данных, которые находятся в окрестности точки х, для которой будет вычисляться значение эмпирической формулы. Такие эмпирические формулы можно назвать «локальными».
Для построения «локальных» эмпирических зависимостей в MathCAD включена функция loess(X,Y,d), приближающая исходные данные полиномом второй степени. Формальные параметры X, Y –этомассивы с исходными данными, а параметр 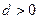 определяет размер области приближаемых данных (рекомендуемое начальное значение 0.75 – 0.85). Чем больше величина d, тем больше сглаживание исходных данных. При больших значениях d работа функции loess(X,Y,d) становится аналогичной функции regress(X,Y,2). Резуль Результатом работы функции loess(X,Y,d) является вектор v, используемый функцией interp(v,X,Y,z), которая вычисляет значение построенной эмпирической формулы в точке z.
определяет размер области приближаемых данных (рекомендуемое начальное значение 0.75 – 0.85). Чем больше величина d, тем больше сглаживание исходных данных. При больших значениях d работа функции loess(X,Y,d) становится аналогичной функции regress(X,Y,2). Резуль Результатом работы функции loess(X,Y,d) является вектор v, используемый функцией interp(v,X,Y,z), которая вычисляет значение построенной эмпирической формулы в точке z.
Пример 1.5. На рис. 1.5 приведен документ MathCAD, реализующий вычислительный эксперимент по построению локальной эмпирической формулы с помощью функции loess(X,Y,d) при 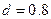 и
и 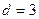 . Из графиков видно, что формула при
. Из графиков видно, что формула при 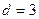 достаточно хорошо приближает полином второго порядка. ¨
достаточно хорошо приближает полином второго порядка. ¨
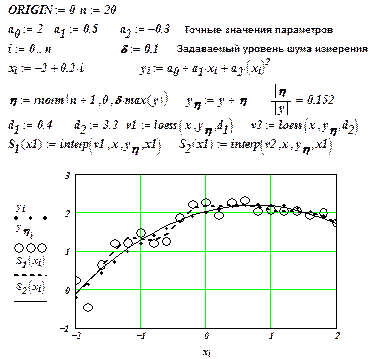
Рис. 1.5. Построение локальных эмпирических зависимостей
 2015-07-21
2015-07-21 6654
6654






