Понятие дифференциала функции
Пусть функция 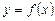 имеет в точке
имеет в точке 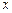 отличную от нуля производную
отличную от нуля производную
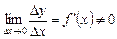 .
.
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать 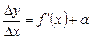 , где
, где 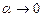 при
при 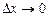 , или
, или 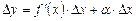 .
.
Таким образом, приращение функции 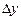 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 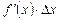 и
и 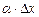 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 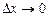 . При этом первое слагаемое есть бесконечно малая функция одного порядка с
. При этом первое слагаемое есть бесконечно малая функция одного порядка с 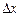 , так как
, так как 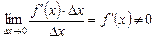 , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем 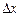 то
то 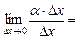
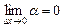 .
.
Поэтому первое слагаемое 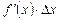 называют главной частью приращения функции
называют главной частью приращения функции 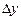 .
.
Дифференциалом функции 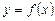 в точке
в точке 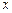 называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 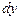 (или
(или 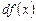 ):
):
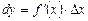 .(1)
.(1)
Дифференциал 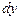 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной 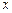 , т. е. дифференциал функции
, т. е. дифференциал функции 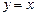 .
.
Так как 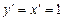 , то, согласно формуле (1), имеем
, то, согласно формуле (1), имеем 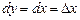 , т. е. дифференциал независимой переменной равен приращению этой переменной:
, т. е. дифференциал независимой переменной равен приращению этой переменной: 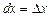 .
.
Поэтому формулу (1) можно записать так
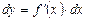 , (2)
, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство 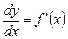 . Теперь обозначение производной
. Теперь обозначение производной 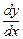 можно рассматривать как отношение дифференциалов
можно рассматривать как отношение дифференциалов 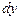 и
и 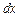 .
.
Пример 1. Найти дифференциал функции 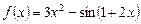 .
.
Решение: По формуле 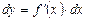 находим
находим 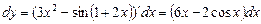 .
.
Пример 2. Найти дифференциал функции 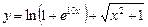 . Вычислить
. Вычислить 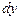 при
при 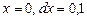 .
.
Решение: 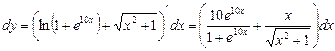 .
.
Подставив 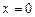 и
и 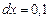 , получим
, получим 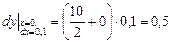 .
.
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для этого проведем к графику функции 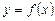 в точке
в точке 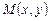 касательную
касательную 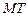 и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки 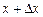 (см. рис.). На рисунке
(см. рис.). На рисунке 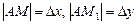 . Из прямоугольного треугольника
. Из прямоугольного треугольника 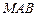 имеем:
имеем: 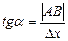 , т.е.
, т.е. 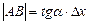 .
.
Но, согласно геометрическому смыслу производной, 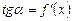 . Поэтому
. Поэтому 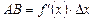 .
.
Сравнивая полученный результат с формулой (1), получаем 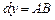 , т. е. дифференциал функции
, т. е. дифференциал функции 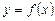 в точке
в точке 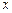 равен приращению ординаты касательной к графику функции в этой точке, когда
равен приращению ординаты касательной к графику функции в этой точке, когда 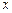 получит приращение
получит приращение 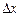 .
.
 В этом и состоит геометрический смысл дифференциала.
В этом и состоит геометрический смысл дифференциала.
Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (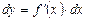 ) и соответствующие теоремы о производных.
) и соответствующие теоремы о производных.
Например, так как производная функции 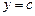 равна нулю, то дифференциал постоянной величины равен нулю:
равна нулю, то дифференциал постоянной величины равен нулю: 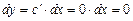 .
.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.
Таблица дифференциалов
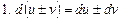
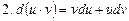 , в частности
, в частности 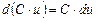
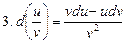 , в частности
, в частности 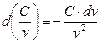
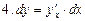 , если
, если 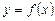
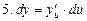 , если
, если 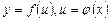
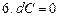
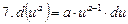
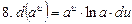 , в частности
, в частности 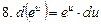
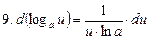 , в частности
, в частности 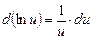
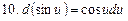
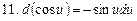
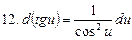
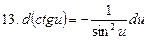
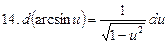
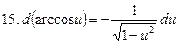
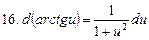
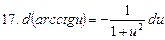
Применение дифференциала к приближенным вычислениям
Как уже известно, приращение 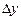 функции
функции 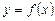 в точке
в точке 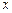 можно представить в виде
можно представить в виде 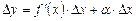 , где
, где 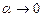 при
при 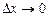 , или
, или 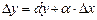 . Отбрасывая бесконечно малую
. Отбрасывая бесконечно малую 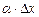 более высокого порядка, чем
более высокого порядка, чем 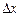 , получаем приближенное равенство
, получаем приближенное равенство
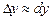 , (3)
, (3)
причем это равенство тем точнее, чем меньше 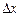 .
.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
Пример 3. Найти приближенное значение приращения функции 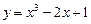 при
при 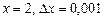 .
.
Решение: Применяем формулу (3) получаем 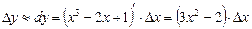 .
.
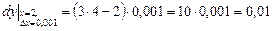
Итак, 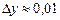 .
.
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем 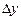 :
:
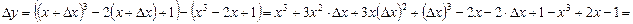
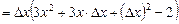 .
.
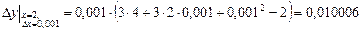
Абсолютная погрешность приближения равна 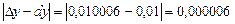 .
.
Подставляя в равенство (3) значения 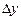 и
и 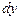 , получим
, получим 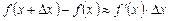 или
или
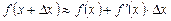 (4)
(4)
Формула (4) используется для вычислений приближенных значений функций.
Пример 4. Вычислить приближенно 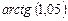 .
.
Решение: Рассмотрим функцию 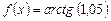 . По формуле (4) имеем
. По формуле (4) имеем 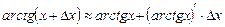 , т. е.
, т. е. 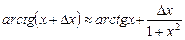 .
.
Так как 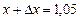 , то при
, то при 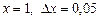 получаем
получаем 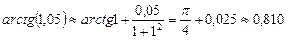 .
.
Пример 5. Вычислить приближенно 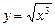 , при
, при 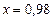 .
.
Решение: Рассмотрим функцию 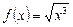 . По формуле (4) имеем
. По формуле (4) имеем 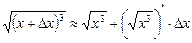 , т. е.
, т. е. 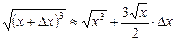 .
.
Так как 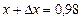 , то при
, то при 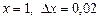 (
(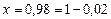 ) получаем
) получаем
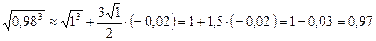 .
.
Пример 6. Какой путь пройдет тело при свободном падении на Луне за 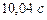 от начала падения. Уравнение свободного падения тела
от начала падения. Уравнение свободного падения тела 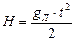 ,
, 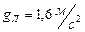 .
.
Решение: Требуется найти 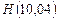 . Воспользуемся приближенной формулой
. Воспользуемся приближенной формулой 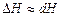 , т.е.
, т.е. 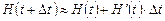 . При
. При 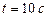 и
и 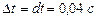 ,
, 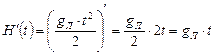 , находим
, находим
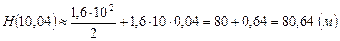 .
.
 2015-07-14
2015-07-14 265
265








