Уравнение Шредингера для атома водорода

Рассмотрим теперь квантово-механическую теорию атомов. Она сохраняет некоторые аспекты старой теории Бора. Например, электроны могут находиться в атоме только в дискретных состояниях с определенной энергией; при переходе электрона из одного состояния в другое испускается или поглощается фотон. Согласно квантовой механике, не существует определенных круговых орбит электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, подобно «облаку» отрицательного заряда.

Применим уравнение Шредингера к электрону, находящемуся в атоме водорода.

Решение задачи об энергетических уровнях электрона для водорода, а также водородоподобных систем сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1), определяется выражением 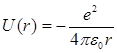(21.20)

и зависит только от r – расстояния между электроном и протоном, поэтому задачу с таким видом потенциальной энергии обычно решают в сферической системе координат. В общем случае волновая функция является функцией от всех координат и уравнение Шредингера будет иметь вид:

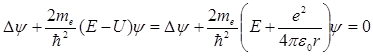. (21.21)

Электрон в атоме находится в потенциальной яме, края которой имеют форму гиперболы (рис.21.5).

Очевидно, что решение этой задачи должно быть подобно решению задачи, когда частица находилась в бесконечно глубокой одномерной потенциальной яме с прямоугольными краями.

Так как электрическое поле – центрально-симметрично, то для решения этого уравнения воспользуемся сферической системой с координатами (r, θ, φ),

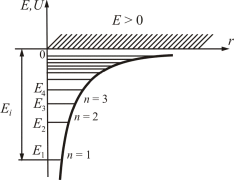Рис.21.5.

которые связаны с декартовыми координатами, как это следует из рис. 21.6, соотношениями: x = r sin θ cos φ; y = r sin θ sin φ; z = r cosθ.

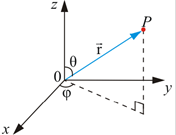Рис. 21.6

Подставив в (21.23) выражение оператора Лапласа в сферических координатах, получим уравнение Шредингера в следующем виде:

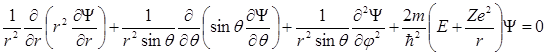. (21.22)

Строгое решение уравнения (21.22) в соответствии с теорией дифференциальных уравнений дает следующие результаты. Электрон в атоме обладает не произвольным значением энергии, а набором определенных отрицательных дискретных значений E _n:

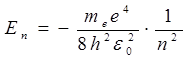, (21.23)

где n – главное квантовое число, принимающее значения 1,2,3.…,∞. Из (21.23) следует, что именно главное квантовое число определяет энергию электрона в атоме: E_n ~ 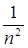. Выражение для значений энергий En (21.23) полностью совпадает с результатами теории Бора (19.15). Для атома водорода значение n = 1 соответствует основному состоянию электрона, значение n = ∞ – свободному электрону (E∞ = 0). Отрицательные значения энергии соответствуют связанному состоянию электрона, когда он находится внутри потенциальной ямы и имеет большие отрицательные значения потенциальной энергии (21.20). Положительными значениями энергии электрон обладает в свободном состоянии, когда он покидает пределы атома, и его энергетический спектр становится непрерывным, т.е. область E > 0 соответствует ионизированному атому.

Оказывается, что одному и тому же значению энергии электрона соответствует несколько различных состояний с разными волновыми функциями, соответствующими различным типам движения электрона. Эти типы движения различаются разными значениями орбитального момента импульса и его проекцией на физически выделенное направление Z, совпадающее с направлением вектора напряженности внешнего магнитного поля.

В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции Ψ n l m s, определяемые набором четырех квантовых чисел: главного n, орбитального l, магнитного m и спинового m _s.

Момент импульса частицы 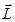относительно начала координат О (центр орбиты электрона на рис. 21.7) в классической механике определяется векторным произведением 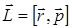, где вектора 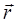и 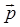являются соответственно радиус-вектором частицы и ее импульсом.

Модуль магнитного момента тока, создаваемого движущимся по орбите электроном, равен 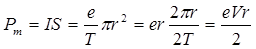. (21.26)

Здесь T – период обращения электрона по орбите, V – его скорость, I − орбитальный ток, S − площадь орбиты.

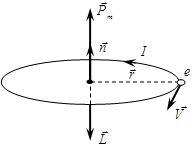Магнитный момент 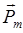обусловлен движением электрона по орбите,

Рис. 21.7

вследствие чего называется орбитальным магнитным моментом электрона.

Электрон обладает массой m _e, поэтому при движении по орбите он обладает моментом импульса 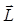, модуль которого 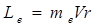. (6.25)

Вектор 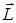называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направление векторов 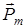и 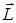противоположны (рис. 21.7).

Отношение магнитного момента элементарной частицы к ее механическому моменту называется орбитальным гиромагнитным отношением. Для электрона оно равно 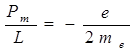. (21.26)

Такая связь между векторами сохраняется и в теории Бора. Поскольку направления векторов 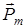и 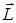противоположны, 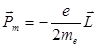. (21.27)

В квантовой механике модуль момента импульса 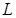движущейся микрочастицы определяется выражением:

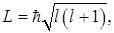(21.28)

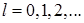. Здесь 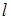– орбитальное квантовое число. Величина 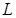является дискретной (квантовой).

В квантовой механике строго доказывается (это следует из решения уравнения Шредингера), что проекция (L _Z) вектора 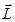на направление вектора напряженности внешнего магнитного поля 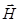, совмещенного с осью Z, может принимать лишь целочисленные значения, кратные постоянной 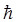: Lz = mħ. (21.29)

Проекция любого вектора не может быть больше модуля этого вектора, т.е. 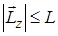. Поэтому в соответствии с выражениями (21.28) и (21.29) имеем:

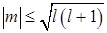, (21.30)

Следовательно, максимальное значение 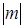равно 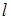, тогда 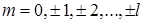. При заданном 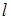число т принимает 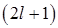значений: 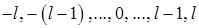, которые образуют спектр проекций 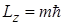на любую выделенную ось 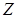, т.е. вектор 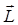может принимать (2 l + 1) ориентаций в пространстве (рис. 21.8).

Таким образом, квантовое число 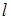определяет как модуль 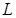момента импульса, так и все возможные значения его проекции на ось 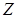. На рис. 6.8 показаны возможные ориентации вектора 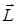и его проекции на выделенное направление 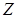магнитного поля. Например, когда орбитальное квантовое число 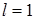(средний рисунок 6.8), то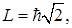 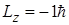; 0; .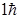

Приведенные результаты, определяющие возможные значения 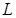и 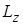, т.е. дискретность в ориентации вектора 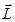, называют пространственным квантованием.

Пространственное квантование на рис. 21.8 представлено лишь схематически (графически): по оси 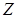откладывают возможные значения mћ, рассматривая их как проекции на ось 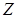вектора 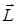длины .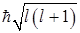

На рис. 21.8 показаны возможные ориентации вектора 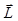в состояниях s, p, d.

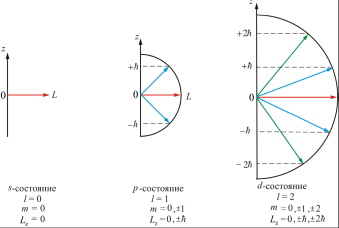
Рис.21.8

Согласно выражениям (21.27), (21.28), (21.29) дискретный спектр разрешенных значений величины модуля орбитального магнитного момента P_m и его проекции на выделенное направление Z для движущегося электрона определяются как

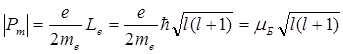и (21. 31)

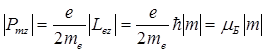. (21. 32)

Ориентация вектора 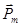в пространстве изображается аналогично вектору 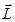, приведенному на рис. 21.8.