В общем случае температура зависит от точки ее замера в пространстве и от времени

Лабораторная работа №1

“Исследование теплопроводности плоской двухслойной стенки”

Цель работы: более глубокое усвоение теории процесса теплопроводности, ознакомление с методикой опытного исследования коэффициентов теплопроводности, получение навыков в постановке эксперимента и в обработке результатов наблюдения.

Теоретические основы эксперимента

Если два тела разной температуры находятся в непосредственном состоянии с друг другом, то передачу тепла от более нагретого к менее нагретому называют теплопроводностью. Аналитическая теории теплопроводности рассматривает любое тело или вещество как сплошную среду, то есть континуум, а не как состоящую из совокупности большого числа дискретных частиц. Это достаточно верно, когда размеры дифференциальных объемов, рассматриваемых при решении задач, значительно превосходят размеры молекулы и межмолекулекулярные расстояния.

В газах процесс переноса энергии осуществляется путем диффузии молекул и атомов, в жидкостях и неметаллах (диэлектриках) путем упругих волн, в металлах же путем диффузии электронов. Чистая теплопроводность в жидкостях и газах практически отсутствует, так как ей всегда будет сопутствовать процесс конвекции.

В общем случае температура зависит от точки ее замера в пространстве и от времени

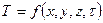(1.1)

Уравнение (1.1) представляет собой аналитически записанную совокупность мгновенных значений температуры во всех точках изучаемого пространства

Эта совокупность будет представлять собой температурное поле, зависящее от времени.

Если температурное поле с течением времени остается неизменным, то имеет место случай стационарного температурного поля.

Если же температура в изучаемом пространстве изменяется не только от точки от точке, но и во времени, то такое поле будет соответствовать неустановившемуся тепловому режиму теплопроводности. Поле температур в этом случае будет также нестационарным. В общем случае уравнение такого поля записано выше (1.1).

Кроме того, в зависимости от числа координат, являющихся аргументами функции температуры, поле может быть одномерным, двухмерным и трехмерным.

Геометрическое место точек, имеющих равные температуры, будет называться поверхностью точек равных температур или изотермической поверхностью. Если рассечь изотермические поверхности плоскостью, то получим линии равных температур – изотермы.

Изотермы, равно как и изотермические поверхности, не пересекаются между собой и не обрываются внутри поля, если оно непрерывно.

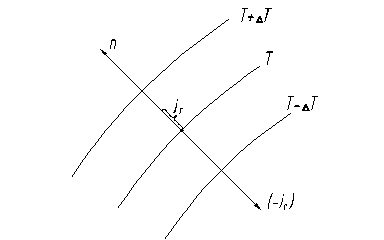
Рисунок 1.1 – Изотермические поверхности

Наибольшее изменение температуры на единицу длины, очевидно, будет происходить по нормали к изотермической поверхности и определяется оно градиентом температуры 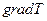. Градиент температуры есть вектор, который направлен по нормали к изотерме в сторону возрастания температуры

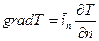, (1.2)

где 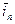- единичный вектор, направленный по нормали к изотермической

поверхности

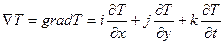(1.3)

Напряженность температурного поля есть вектор, равный по величине, но противоположного направления

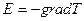(1.4)

Тепло может распространяться лишь в том случае, когда не равен нулю температурный градиент. На основании опытных данных и согласно гипотезе Фурье можно записать, что количество тепла 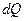, проходящее через элементарную площадку изотермической поверхности 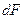за промежуток времени 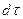, пропорционально температурному градиенту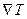

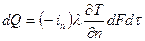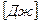, (1.5)

Количество тепла, проходящее через единицу площади изотермической поверхности в единицу времени, называется плотностью теплового потока

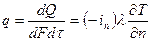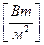, (1.6)

Это и есть основной закон теплопроводности. Читается он так: плотность теплового потока прямо пропорциональна напряженности температурного поля или прямо пропорционально градиенту температуры

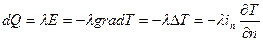, (1.7)

где l - коэффициент пропорциональности, называемый коэффициентом

теплопроводности.

Коэффициент теплопроводности является физической характеристикой тела и указывает на способность тел к переносу тепла за счет теплопроводности.

Из закона Фурье можно заключить, что коэффициент теплопроводности равен количеству тепла, протекающему в единицу времени через единицу поверхности при перепаде температур на единицу длины нормали в один градус.

Для одномерного, стационарного температурного поля будем иметь

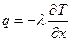
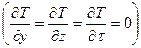(1.8)

Если 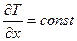, то температура с изменением длины x будет меняться по линейному закону и тогда

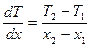(1.9)

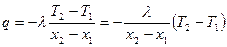(1.10)

Величина 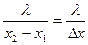называется теплопроводностью, а величина обратная ей

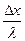- термическим сопротивлением участка тела.

Теплопроводность в газах и парах обусловлена в значительной мере молекулярным переносом кинетической энергии движения молекул. Этим объясняется малая величина коэффициентов теплопроводности [1].

В жидкостях перенос тепла теплопроводностью происходит по типу распространения продольных колебаний, аналогично звуковым волнам. Величины коэффициентов теплопроводности для жидкостей больше, чем для газов и паров.

В металлах перенос тепла при теплопроводности осуществляется за счет наличия и перемещения свободных электронов, которые переносят с собой энергию. При повышении температуры рассеивание электронов увеличивается, и это приводит к снижению коэффициента теплопроводности. Для газов с ростом температуры растет и коэффициент теплопроводности. Для большинства жидкостей с ростом температуры коэффициент теплопроводности l убывает (исключением являются вода и глицерин).

Дифференциальное уравнение теплопроводности выводится на основании общих законов физики для элементарного объема рассматриваемого тела и устанавливает зависимость между температурой T, временем t, координатами x, y, z и физическими параметрами тела. Для нестационарного теплового режима применительно к твердым телам это уравнение имеет вид

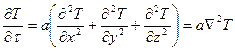, (1.11)

где T – температура, К;

t - время, с;

а – коэффициент температуропроводности, который определяется по

формуле

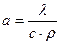, (1.12)

где с – удельная теплоемкость, Дж/кг град;

r - плотность, кг/м³;

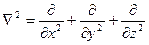- оператор Лапласа.

Коэффициент температуропроводности имеет физический смысл. Покажем это, приведя следующие рассуждения. Можно показать, что для изотермической поверхности справедливо следующее соотношение

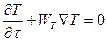, (1.13)

где W_T – скорость распространения изотермической поверхности.

Воспользовавшись дифференциальным уравнением теплопроводности, получим

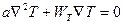(1.14)

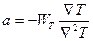(1.15)

и окончательно, то есть коэффициент температуропроводности пропорционален скорости распространения изотермической поверхности, а величина, обратная коэффициенту температуропроводности

Дифференциальное уравнение теплопроводности описывает процесс в целом. Постановка и решение конкретных задач при изучении теплопроводности могут быть получены из дифференциального уравнения теплопроводности при помощи условий однозначности.

Условия однозначности позволяют из бесчисленного числа возможных процессов выделить интересующий нас и дать ему математическое описание.

Условия однозначности включают в себя:

1. геометрические, учитывающие форму и размер тела;

2. физические, характеризующие физические свойства тела;

3. временные, характеризующие протекание процесса во времени;

4. граничные, определяющие взаимодействие рассматриваемого тела с окружающей средой.

Рассмотрим условия однозначности применительно к задаче о теплопроводности плоской стенки (рисунок 1.2).

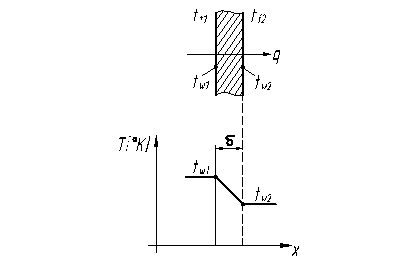
Рисунок 1.2 – Теплопроводность плоской стенки

Будем считать, что толщина стенки пренебрежимо мала по сравнению с другими ее размерами. Это условие приводит к тому, что можно пренебречь теплоотводом с торцев и считать, что удельный тепловой поток q направлен перпендикулярно стенке, как показано на рисунке 1.2. То есть разбор геометрических условий однозначности позволил несколько упростить дифференциальное уравнение термодинамики для рассматриваемого случая, свести задачу к одномерной. Физические условия однозначности заключаются в том, что известен материал стенки и все его физические параметры, в том числе и l.

Временные условия однозначности заключаются в том, что рассматривается стационарный режим, то есть .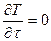

Граничные условия однозначности могут быть трех родов: при граничных условиях первого рода должно быть известным распределение температуры по поверхности тела, то есть, известны значения температур стенк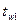и и 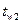. Задача сводится к определению величины удельного теплового потока по формуле

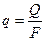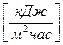, (1.16)

При граничных условиях первого рода заданы величины удельного теплового потока и одна из температур поверхносте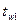й или 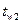необходимо определить неизвестную температуру стенки.

При граничных условиях третьего рода определяется величина удельного теплового потока q, когда известны температуры сред, омывающих стенку 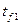и 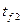, и коэффициенты теплоотдачи. Последний случай описывает сложный теплообмен, обычно планируемый теплопередачей.

Решая дифференциальное уравнение теплопроводности с учетом условий однозначности, можно получить, что распределение температур в плоской стенке подчиняется закону прямой.

Действительно, для задачи с граничными условиями первого рода при передаче тепла через плоскую стенку на стационарном режиме будем иметь

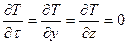(1.17)

Дифференциальное уравнение теплопроводности примет вид

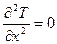(1.18)

Температура изменяется лишь в направлении перпендикулярном плоскости стенки.

Граничные условия:

при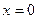

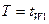
при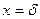

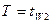
После двойного интегрирования с использованием граничных условий получим

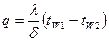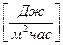, (1.19)

Разность температур 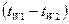называют температурным напором. Для граничных условий второго рода на основании полученного выражения можно записать

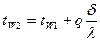(1.20)

или

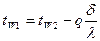(1.21)

Для многослойной стенки величина удельного теплового потока для граничных условий первого рода может быть определена по уравнению

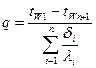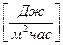, , (1.22)

где 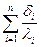- термическое сопротивление многослойной стенки, равное

сумме термических сопротивлений отдельных слоев;

n – число слоев (рисунок 1.3).

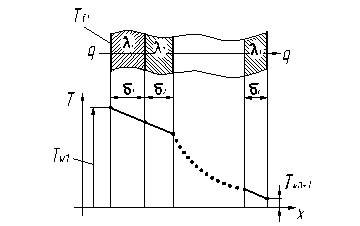
Рисунок 1.3 – Распределение температур

Для граничных условий второго рода задача может быть решена

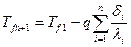(1.23)

или

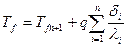(1.24)

В каждом из слоев распределение температур происходит по линейному закону. Наклон прямой распределения температур зависит от термического сопротивления слоя.

При толщине d слоев температурный напор больше в том из слоев, который обладает большим термическим сопротивлением или меньшим коэффициентом теплопроводности.