Док-во

Обозначим X ₁ – число появлений события A в 1^ом испытании

X ₂ – число появлений события A в 2^ом испытании

..........................................................................................

X_n – число появлений события A в n ^ом испытании

Законы распределения 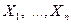одинаковы, а именно

X_i=0,– событие А не появилось в i ^ом испытании

X_i=1,– событие А появилось в i ^ом испытании
i =1, 2,..., n

M(X_i)=p; D(X_i)=0×q+1×p-p²=p-p²=pq

X ₁+ X ₂ +...+ X_n=m – столько раз появилось A в n испытаниях.

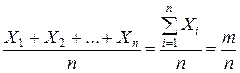– относительная частота события A.

Применим частный случай теоремы Чебышева

1) 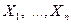– попарно независимые (вып-ся)

2) имеют одно и то же математическое ожидание, M(X_i)=p,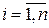

3) дисперсии равномерно ограничены

Действительно: D (X_i) = pq = p – p ², 0< p <1, i =1, 2,..., n

D’ (X_i)=1 – 2 p, D’ (X_i)=0 Þ p = ½

Единственный экстремум, max Þ при p = ½ наибольшее значение

D_{наиб .}= ½ × ½= ¼, D(X_i) £¼ – равномерно ограничены. Тогда, по теореме Чебышева

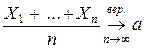или 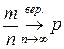, что и требовалось доказать.

Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности.