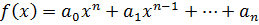 .
.
Первой производной многочлена  называется многочлен вида:
называется многочлен вида:
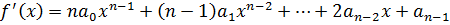 .
.
Второй производной многочлена  называется производная от первой производной многочлена
называется производная от первой производной многочлена  :
:
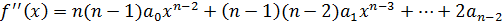 .
.
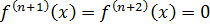
Для многочленов справедливы правила дифференцирования:
1) 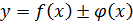 ;
;
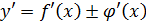 .
.
2) 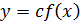 ;
;
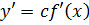 .
.
3) 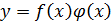 ;
;
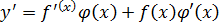 .
.
4) 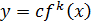 ;
;
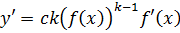 .
.
Теорема о кратном множителе многочлена 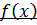 :
:
Если 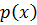 является k-кратным множителем в разложении многочлена
является k-кратным множителем в разложении многочлена  над P, то этот многочлен будет являться множителем (k-1) кратности в разложении его производной
над P, то этот многочлен будет являться множителем (k-1) кратности в разложении его производной 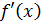 .
.
Доказательство:
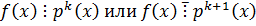
ð 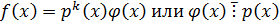
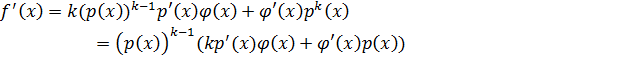
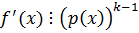
Покажем, что 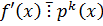 .
.
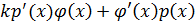
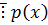
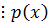
Сумма 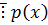 .
.
Многочлен 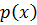 для
для  является (k-1)-кратным.
является (k-1)-кратным.
Теорема о k-кратном корне многочлена 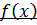 :
:
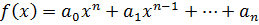 , c – k-кратный корень многочлена
, c – k-кратный корень многочлена  .
.
Всякое число с, являющееся корнем k-кратности многочлена  , является корнем его производной кратности (k-1).
, является корнем его производной кратности (k-1).
Доказательство:
Дано: c – k-кратный корень.
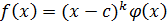
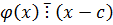
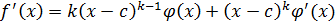
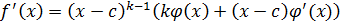
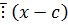
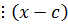
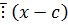
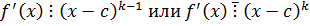
c – корень (k-1) кратности.
Пример: 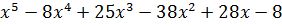 ,
, 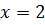
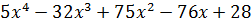
| -32 | -76 | ||||
| -22 | -14 |
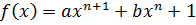 .
.
с=1 – корень.
Следствие:
1) 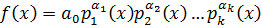
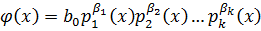
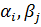 - могут быть нулями.
- могут быть нулями.
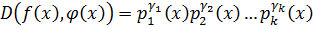 .
.
Произведение всех общих множителей, входящих в разложение каждого из них:
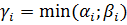 .
.
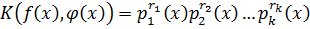 ,
,
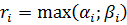
произведение неприводимых множителей, входящих в разложение хотя бы одного.
Учитывая теорему о k-кратном множителе многочлена  можно доказать следующую теорему.
можно доказать следующую теорему.
2) Многочлен  не имеет кратных множителей ó
не имеет кратных множителей ó 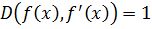 .
.
Доказательство:
Пусть дан многочлен 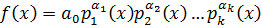 .
.
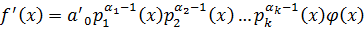 .
.
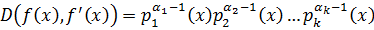 .
.
Дано: многочлен 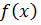 не имеет кратных множителей.
не имеет кратных множителей.
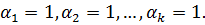
В произведение будут входить в 0-ой степени.
Тогда 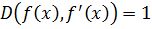 .
.
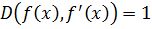 . => Значит каждый
. => Значит каждый 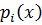 в разложение
в разложение 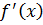 входит в 0-ой степени, значит, в сам многочлен он войдет в 1 степени.
входит в 0-ой степени, значит, в сам многочлен он войдет в 1 степени.
Пример: 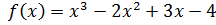
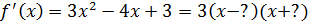
Есть ли кратные неприводимые множители?
D<0. Найти НОД.
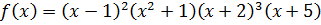
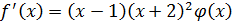
 - 4-ой степени.
- 4-ой степени.
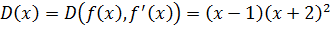 .
.
 2015-08-13
2015-08-13 3561
3561
