Минимизация на заданном множестве. Теорема о существовании решения

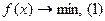
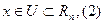, тут f(x) – функция многих переменных.

Если U - компактное, тогда существует точка 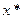, в котором н/п ф-я f(x) достигает своего наименьшего значения.

Теорема. Если ф-я f(x) н/п в замкнутом множестве U, и для некоторого 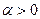выполняется, что на подмножестве 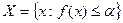, непустом и ограниченом, то задача (1), (2) имеет решения.

Доказательство. Т.к. м-во Х задается нестрогим неравенством, 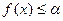, то это множество замкнутое. Покажем это: Пусть 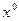- некоторая предельная точка м-ва Х, то всегда существ. некоторая ее 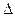-окрестность, которая содержит точки из Х. Тогда если взять 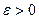, найдутся точки м-ва Х, для которых 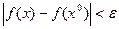=> сущест. 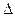- окрестность в пересечении с м-вом U дающая непустое м-во. Можем найти 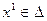-окрестности и .

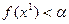Тогда можем получить, что 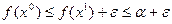. Тоесть м-во Х буд. замкнутым и ф-ция будет определена и на границе. Если м-во U выпукло, то минимум единственный.