Реализуем 10 циклов обучения. Для этого можно использовать функции train или adapt:
net.trainParam.epochs = 10;
net = train(net,p);
net.adaptParam.passes = 10;
[net,y,e] = adapt(net,mat2cell(p));
Заметим, что для сетей с конкурирующим слоем по умолчанию используется обучающая функция trainwb1, которая на каждом цикле обучения случайно выбирает входной вектор
и предъявляет его сети; после этого производится коррекция весов и смещений.
Выполним моделирование сети после обучения:
a = sim(net,p);
ac = vec2ind(a)
ac = 2 1 2 1
Видим, что сеть обучена классификации векторов входа на 2 кластера: первый расположен в окрестности вектора (0, 0), второй – в окрестности вектора (1, 1). Результирующие веса и смещения равны:
wts1 = net.IW{1,1}
b1 = net.b{1}
wts1 =
0.58383 0.58307
0.41712 0.42789
b1 = 5.4152
5.4581
Заметим, что первая строка весовой матрицы действительно близка к вектору (1, 1),
в то время как вторая строка близка к началу координат. Таким образом, сформированная сеть обучена классификации входов. В процессе обучения каждый нейрон в слое, весовой вектор которого близок к группе векторов входа, становится определяющим для этой группы векторов. В конечном счете, если имеется достаточное число нейронов, каждая группа векторов входа будет иметь нейрон, который выводит 1, когда представлен вектор этой группы, и 0 в противном случае, или, иными словами, формируется кластер. Таким образом, слой Кохонена действительно решает задачу кластеризации векторов входа.
Пример:
Функционирование слоя Кохонена можно пояснить более наглядно, используя графику системы MATLAB. Рассмотрим 48 случайных векторов на плоскости, формирующих 8 кластеров, группирующихся около своих центров. На графике, приведенном на рис. 7.3, показано 48 двухэлементных векторов входа.
Сформируем координаты случайных точек и построим план их расположения
на плоскости:
c = 8; n = 6; % Число кластеров, векторов в кластере
d = 0.5; % Среднеквадратичное отклонение от центра кластера
x = [–10 10;–5 5]; % Диапазон входных значений
[r,q] = size(x); minv = min(x')'; maxv = max(x')';
v = rand(r,c).*((maxv – minv)*ones(1,c) + minv*ones(1,c));
t = c*n; % Число точек
v = [v v v v v v]; v=v+randn(r,t)*d; % Координаты точек
P = v;
plot(P(1,:), P(2,:),'+k') % Рис.7.3
title(' Векторы входа'), xlabel('P(1,:)'), ylabel('P(2,:)')
Векторы входа, показанные на рис. 7.3, относятся к различным классам.
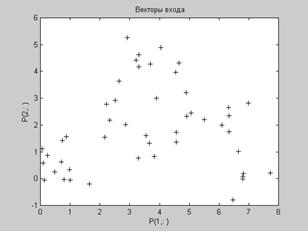 Рис. 7.3
Рис. 7.3
Применим конкурирующую сеть из восьми нейронов для того, чтобы распределить их по классам:
net = newc([–2 12;–1 6], 8,0.1);
w0 = net.IW{1}
b0 = net.b{1}
c0 = exp(1)./b0
Начальные значения весов, смещений и параметров активности нейронов представлены в следующей таблице:
| w0 = 0.5 0.25 0.5 0.25 0.5 0.25 0.5 0.25 0.5 0.25 0.5 0.25 0.5 0.25 0.5 0.25 | b0 = 21.746 21.746 21.746 21.746 21.746 21.746 21.746 21.746 | c0 = 0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125 |
После обучения в течение 500 циклов получим:
net.trainParam.epochs = 500;
net = train(net,P);
w = net.IW{1}
bn = net.b{1}
cn = exp(1)./bn
| w = 6.2184 2.4239 1.3277 0.94701 0.31139 0.40935 3.543 4.5845 3.4617 2.8996 4.3171 1.4278 6.7065 0.43696 0.97817 0.17242 | bn = 22.137 21.718 21.192 21.472 21.957 21.185 23.006 21.42 | cn = 0.123 0.125 0.128 0.127 0.124 0.128 0.118 0.127 |
Как следует из приведенных таблиц, центры кластеризации распределились по восьми областям, показанным на рис. 7.4, а; смещения отклонились в обе стороны от исходного значения 21.746 так же, как и параметры активности нейронов, показанные на рис. 7.4, б.
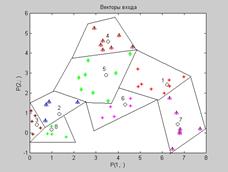 а
а
| 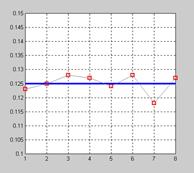 б
б
|
Рис. 7.4
Рассмотренная самонастраивающаяся сеть Кохонена является типичным примером сети, которая реализует процедуру обучения без учителя.
Демонстрационный пример democ1 также поясняет процедуру обучения самоорганизующейся сети.
 2015-08-21
2015-08-21 263
263








