Определение 15.2. Квадратичная форма называется канонической (или имеет канонический вид), если все aij = 0 при i ¹ j. Таким образом, канонический вид квадратичной формы следующий:
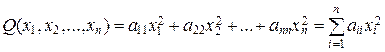 .
.
Очевидно, что канонической квадратичной форме соответствует диаго-нальная матрица
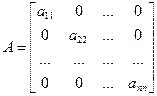 = diag (а 11, а 22,…, аnn).
= diag (а 11, а 22,…, аnn).
Нахождение канонического вида квадратичной формы называется приведением формы к каноническому виду.
Теоремa 15.1. Любая квадратичная форма с помощью ортогонального преобразования может быть приведена к каноническому виду
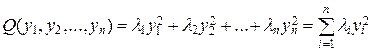 , (15.3)
, (15.3)
где l 1, l 2,…, ln – собственные значения матрицы квадратичной формы.
Доказательство. Так как матрица А квадратичной формы является сим-метрической, то в силу теоремы 14.2 для нее существует ортогональная матрица Т, такая, что выполнено равенство L = Т * АТ. Пусть x = Т y, y = (у 1, у 2,…, уn), где у 1, у 2,…, уn – это координаты x в новом базисе, состоящем из нормированных собственных векторов матрицы А. Тогда из соотношения (15.2) получаем
Q (x 1, x 2,…, xn) = (x, А x) = (T y, А (Т y)) = (y, (Т * АТ) y) = (y, L y) = 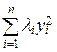 , y = Т * x. (15.4)
, y = Т * x. (15.4)
|
|
|
Таким образом, квадратичная форма в базисе, состоящем из ортонорми-рованных собственных векторов матрицы А, приводится к каноническому виду. Алгоритм приведения ее к каноническому виду заключается, очевидно, в диагонализации симметрической матрицы квадратичной формы и последующей записи квадратичной формы в виде (15.3).¨
Пример 3. Привести к каноническому виду квадратичную форму
Q (x 1, x 2, x 3, x 4) = 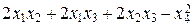 .
.
Решение. Составим соответствующую этой форме матрицу
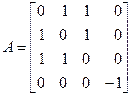 .
.
Характеристическое уравнение 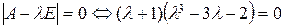 имеет корни l 1 = 2, l 2 = l 3 = l 4= – 1. Для l 1 = 2 и l 2 = – 1 находим собственные векторы (см. аналогичный пример 1 из §12.2) v 1 = (1, 1, 1, 0) и v 2 = (0, – 1, 1, 0) соответственно. Собственные векторы v 3 и v 4, соответствующие собственному значению l 3 = l 4= – 1, найдем из следующих соображений: по теореме 12.4 собственные векторы v 1, v 2, v 3, v 4 можно выбрать попарно ортогональными. Если v = (v 1, v 2, v 3, v 4) – произвольный вектор, ортогональный v 1 и v 2, то для определения его координат получаем систему уравнений
имеет корни l 1 = 2, l 2 = l 3 = l 4= – 1. Для l 1 = 2 и l 2 = – 1 находим собственные векторы (см. аналогичный пример 1 из §12.2) v 1 = (1, 1, 1, 0) и v 2 = (0, – 1, 1, 0) соответственно. Собственные векторы v 3 и v 4, соответствующие собственному значению l 3 = l 4= – 1, найдем из следующих соображений: по теореме 12.4 собственные векторы v 1, v 2, v 3, v 4 можно выбрать попарно ортогональными. Если v = (v 1, v 2, v 3, v 4) – произвольный вектор, ортогональный v 1 и v 2, то для определения его координат получаем систему уравнений
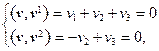
общее решение которой имеет вид
v = 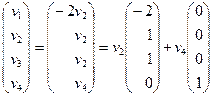 ,
,
где v 2 и v 4 – произвольные действительные числа.
Таким образом, любой вектор v, ортогональный v 1 и v 2, является линейной комбинацией векторов v 3 = (– 2, 1, 1, 0) и v 4 = (0, 0, 0, 1). Попарная ортогональность векторов v 1, v 2, v 3, v 4 очевидна. Итак, найдены все четыре попарно ортогональных собственных вектора матрицы A. Нормируя их, получим векторы
u 1 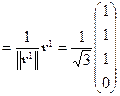 , u 2
, u 2 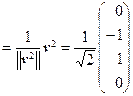 , u 3
, u 3 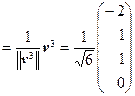 , u 4
, u 4 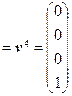 ,
,
которые являются столбцами матрицы ортогонального преобразования Т, т. е.
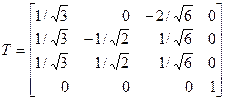 .
.
Тогда в силу формулы (15.4) квадратичная форма Q в базисе u 1, u 2, u 3, u 4 приводится к каноническому виду
Q (y 1, y 2, y 3, y 4) = 2 y 12 – y 22 – y 32 – y 42.·
 2015-08-21
2015-08-21 10060
10060
