Рассмотрим следующую ситуацию, с которой вы сталкиваетесь каждый день. Предположим, что вы собрались в магазин канцелярских товаров. Ваша задача сделать как можно больше покупок при условии, что вы покупаете только 3 разновидности товара, а именно ручки, карандаши и блокноты (если рассматривать весь ассортимент товара, размерность задачи значительно увеличится, при наличии достаточного количества свободного времени можете попытаться ее решить). В кармане у вас 50 у.е. и, кроме всего прочего, вам необходимо купить хотя бы 3 ручки и 2 блокнота. Вполне закономерно, что вам известна цена товаров: 10 - ручка, 5 - ка-рандаш и 20 у.е. - блокнот.
Если вы обладаете достаточными аналитическими способностями, то сразу сможете сделать вывод по поводу решения данной задачи, но, в качестве примера, попытаемся решить ее симплекс-методом.
Решение:
Если обозначить за Х1 - количество приобретаемых в магазине ручек, за Х2 - карандашей, а за Х3 - блокнотов, то исходную задачу можно представить в следующем виде:
Максимизировать
L(X)=X1+X2+X3
при ограничениях
10* X1+5* X2+20*X3 <= 50,
X1 >= 3,
X3 >= 2,
X1, X2, X3 >= 0.
После приведения к каноническому виду задача примет вид:
максимизировать
L(X)=X1+X2+X3
при ограничениях
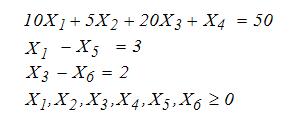
При определении начального опорного плана сталкиваемся с отсутствием единичной подматрицы и, следовательно, вводим искусственные переменные и переходим к М-задаче (M→∞):
максимизировать
L(X)=X1+X2+X3-M*X7-M*X8
при ограничениях
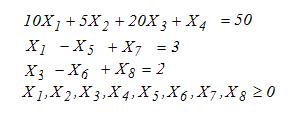
Отыскав таким образом единичный начальный базис Б0=(А4, А7, А8), переходим к построению симплексных таблиц.
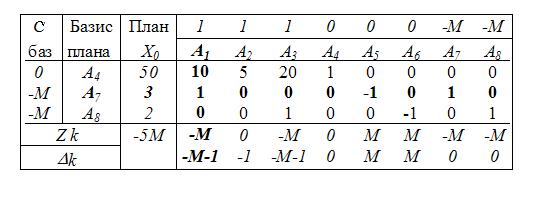
Если принять во внимание, что М - это большое положительное число, то из данной таблицы видно, что опорный план не оптимален (не все *k>0 и хотя бы одно из значений Zjk >0).
Рассчитываем
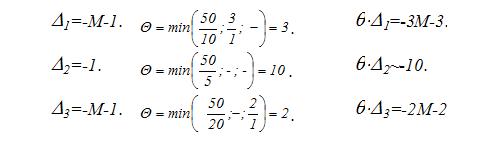
Вводя в базис А1 вместо А7, получаем новую симплексную таблицу. 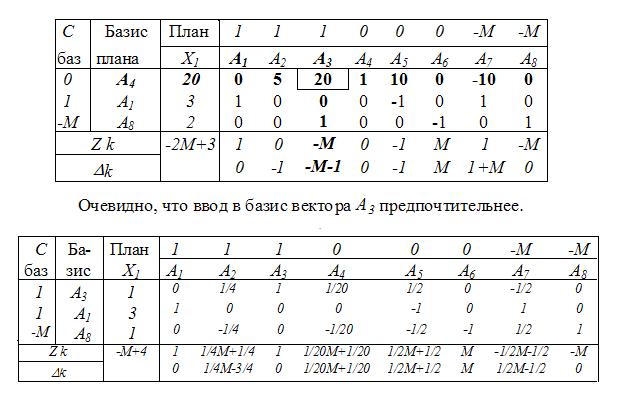
Из таблицы видно, что данный опорный план оптимален. Однако в базисе находится искусственная переменная и она не равна нулю, отсюда заключаем, что в исходной задаче противоречивые ограничения.
Если вспомнить о происхождении решенной задачи, то при указанном количестве денег в кармане вам необходимо "умерить свой аппетит".
Варианты заданий для самостоятельной работы
Решить задачу классическим симплекс-методом. Объяснить полученные результаты.



Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей, как мы уже знаем, в нахождении максимального значения функции
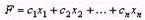 (32)
при условиях (32)
при условиях
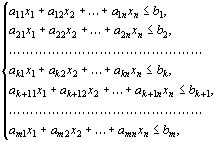 (33) (33)
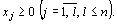 (34)
Определение 13.
Задача, состоящая в нахождении минимального значения функции (34)
Определение 13.
Задача, состоящая в нахождении минимального значения функции
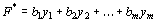 (35)
при условиях (35)
при условиях
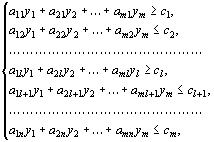 (36) (36)
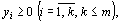 (37)
называется двойственной по отношению к задаче (32) – (34). Задачи (32) – (34) и (35) – (37) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:
1. Целевая функция исходной задачи (32) – (34) задается на максимум, а целевая функция двойственной (35) – (37) – на минимум.
2. Матрица (37)
называется двойственной по отношению к задаче (32) – (34). Задачи (32) – (34) и (35) – (37) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:
1. Целевая функция исходной задачи (32) – (34) задается на максимум, а целевая функция двойственной (35) – (37) – на минимум.
2. Матрица
 (38)
составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) – (34), и аналогичная матрица (38)
составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) – (34), и аналогичная матрица
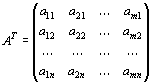 (39)
в двойственной задаче (35) – (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками).
3. Число переменных в двойственной задаче (35) – (37) равно числу ограничений в системе (33) исходной задачи (32) – (34), а число ограничений в системе (36) двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) – (37) являются свободные члены в системе (33) исходной задачи (32) – (34), а правыми частями в соотношениях системы (36) двойственной задачи – коэффициенты при неизвестных в целевой функции (32) исходной задачи.
5. Если переменная xj исходной задачи (32) – (34) может принимать только лишь положительные значения, то j –е условие в системе (36) двойственной задачи (35) – (37) является неравенством вида “? ”. Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) – (34) и переменными двойственной задачи (35) – (37). Если i – соотношение в системе (33) исходной задачи является неравенством, то i –я переменная двойственной задачи (39)
в двойственной задаче (35) – (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками).
3. Число переменных в двойственной задаче (35) – (37) равно числу ограничений в системе (33) исходной задачи (32) – (34), а число ограничений в системе (36) двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) – (37) являются свободные члены в системе (33) исходной задачи (32) – (34), а правыми частями в соотношениях системы (36) двойственной задачи – коэффициенты при неизвестных в целевой функции (32) исходной задачи.
5. Если переменная xj исходной задачи (32) – (34) может принимать только лишь положительные значения, то j –е условие в системе (36) двойственной задачи (35) – (37) является неравенством вида “? ”. Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) – (34) и переменными двойственной задачи (35) – (37). Если i – соотношение в системе (33) исходной задачи является неравенством, то i –я переменная двойственной задачи 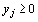 . В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (33) прямой задачи и соотношения (36) двойственной задачи являются неравенствами вида “ . В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (33) прямой задачи и соотношения (36) двойственной задачи являются неравенствами вида “ 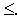 ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Пример 11.
Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Пример 11.
Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
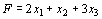 (40)
при условиях (40)
при условиях
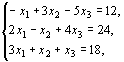 (41) (41)
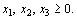 (42)
Решение. Для данной задачи (42)
Решение. Для данной задачи
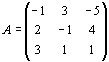 и и 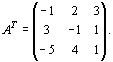 Число переменных в двойственной задаче равно числу уравнений в системе (41), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (41), т.е. числа 12, 24, 18.
Целевая функция исходной задачи (40) – (42) исследуется на максимум, а система условий (41) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (40) – (42) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “? ”. Следовательно, для задачи (40) – (42) двойственная задача такова: найти минимум функции
Число переменных в двойственной задаче равно числу уравнений в системе (41), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (41), т.е. числа 12, 24, 18.
Целевая функция исходной задачи (40) – (42) исследуется на максимум, а система условий (41) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (40) – (42) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “? ”. Следовательно, для задачи (40) – (42) двойственная задача такова: найти минимум функции 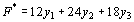 при условиях при условиях
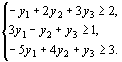 Пример 12.
Для задачи, состоящей в максимизации функции
Пример 12.
Для задачи, состоящей в максимизации функции
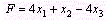 при условиях
при условиях
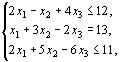
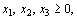 сформулировать двойственную задачу.
Решение. Для данной задачи
сформулировать двойственную задачу.
Решение. Для данной задачи
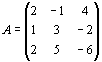 , , 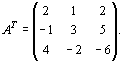 В соответствии с общими правилами задача, двойственная по отношению к данной, формулируется следующим образом: найти минимум функции
В соответствии с общими правилами задача, двойственная по отношению к данной, формулируется следующим образом: найти минимум функции 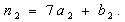 при условиях при условиях
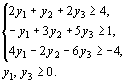 Связь между решениями прямой и двойственной задач. Рассмотрим пару двойственных задач, образованную основной задачей линейного программирования и двойственной к ней. Исходная задача: найти максимум функции
Связь между решениями прямой и двойственной задач. Рассмотрим пару двойственных задач, образованную основной задачей линейного программирования и двойственной к ней. Исходная задача: найти максимум функции
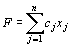 (43)
при условиях (43)
при условиях
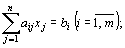 (44) (44)
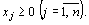 (45)
Двойственная задача: найти минимум функции (45)
Двойственная задача: найти минимум функции
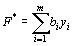 (46)
при условиях (46)
при условиях
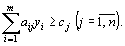 (47)
Каждая из задач двойственной пары (43) – (45) и (46), (47) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1.
Если Х – некоторый план исходной задачи (43) – (45), a Y – произвольный план двойственной задачи (46), (47), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е. (47)
Каждая из задач двойственной пары (43) – (45) и (46), (47) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1.
Если Х – некоторый план исходной задачи (43) – (45), a Y – произвольный план двойственной задачи (46), (47), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е. 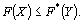 Лемма 2.
Если
Лемма 2.
Если 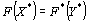 для некоторых планов X* и Y* задач (43) – (45) и (46), (47), то X* – оптимальный план исходной задачи, а Y* – оптимальный план двойственной задачи.
Теорема 8
(первая теорема двойственности). Если одна из задач двойственной пары (43) – (45) или (46), (47) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. для некоторых планов X* и Y* задач (43) – (45) и (46), (47), то X* – оптимальный план исходной задачи, а Y* – оптимальный план двойственной задачи.
Теорема 8
(первая теорема двойственности). Если одна из задач двойственной пары (43) – (45) или (46), (47) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. 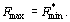 Если же целевая функция одной задачи из двойственной пары неограничена (для исходной (43) – (45) – сверху, для двойственной (46), (47) – снизу), то другая задача вообще не имеет планов.
Теорема 9
(вторая теорема двойственности).
План
Если же целевая функция одной задачи из двойственной пары неограничена (для исходной (43) – (45) – сверху, для двойственной (46), (47) – снизу), то другая задача вообще не имеет планов.
Теорема 9
(вторая теорема двойственности).
План 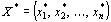 задачи (43) – (45) и план задачи (43) – (45) и план 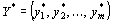 задачи (46), (47) являются оптимальными планами этих задач тогда и только тогда, когда для любого задачи (46), (47) являются оптимальными планами этих задач тогда и только тогда, когда для любого 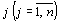 выполняется равенство выполняется равенство
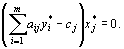 Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев: 1) обе задачи имеют планы; 2) планы имеет только одна задача; 3) для каждой задачи двойственной пары множество планов пусто.
Пример 13.
Для задачи, состоящей в определении максимального значения функции
Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев: 1) обе задачи имеют планы; 2) планы имеет только одна задача; 3) для каждой задачи двойственной пары множество планов пусто.
Пример 13.
Для задачи, состоящей в определении максимального значения функции 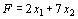 при условиях при условиях
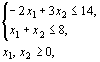 составить двойственную задачу и найти решение обеих задач.
Решение. Двойственной задачей по отношению к исходной является задача, состоящая в определении минимального значения функции
составить двойственную задачу и найти решение обеих задач.
Решение. Двойственной задачей по отношению к исходной является задача, состоящая в определении минимального значения функции 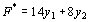 при условиях при условиях
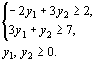 Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию задачи линейного программирования (рис. 7 и 8).
Как видно из рис. 8, максимальное значение целевая функция исходной задачи принимает в точке В. Следовательно, Х*= (2, 6) является оптимальным планом, при котором
Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию задачи линейного программирования (рис. 7 и 8).
Как видно из рис. 8, максимальное значение целевая функция исходной задачи принимает в точке В. Следовательно, Х*= (2, 6) является оптимальным планом, при котором 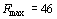 . Минимальное значение целевая функция двойственной задачи принимает в точке Е (рис. 8). Значит, Y *=(1; 4) является оптимальным планом двойственной задачи, при котором . Минимальное значение целевая функция двойственной задачи принимает в точке Е (рис. 8). Значит, Y *=(1; 4) является оптимальным планом двойственной задачи, при котором 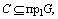 Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой. Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.
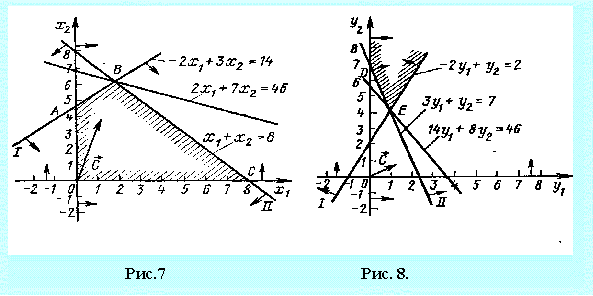 Из рис. 7 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис. 8, значение целевой функции двойственной задачи при любом ее плане не меньше 46. Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи при ее произвольном плане.
Пример 14.
Найти решение двойственной пары задач.
Исходная задача;
Из рис. 7 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис. 8, значение целевой функции двойственной задачи при любом ее плане не меньше 46. Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи при ее произвольном плане.
Пример 14.
Найти решение двойственной пары задач.
Исходная задача;
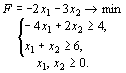 Двойственная задача:
Двойственная задача:
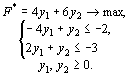 Решение. Как исходная, так и двойственная задача содержат по две переменные. Поэтому их решение находим, используя геометрическую интерпретацию задачи линейного программирования (рис. 7 и 8). Из рис. 7 видно, что исходная задача не имеет оптимального плана из-за неограниченности снизу ее целевой функции на множестве допустимых решений.
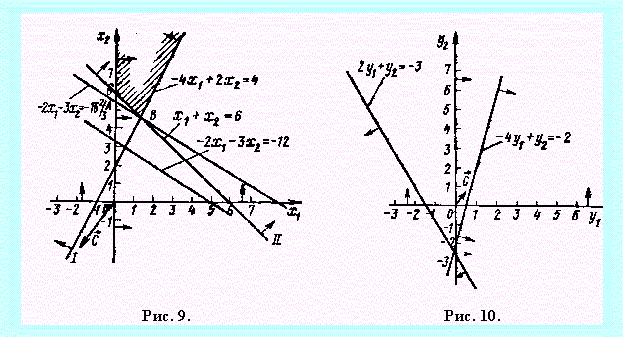
Из рис. 10 следует, что двойственная задача не имеет планов, поскольку многоугольник решений ее пуст. Это означает, что если исходная задача двойственной пары не имеет оптимального плана из-за неограниченности на множестве допустимых решений ее целевой функции, то двойственная задача также не имеет планов.
Решение. Как исходная, так и двойственная задача содержат по две переменные. Поэтому их решение находим, используя геометрическую интерпретацию задачи линейного программирования (рис. 7 и 8). Из рис. 7 видно, что исходная задача не имеет оптимального плана из-за неограниченности снизу ее целевой функции на множестве допустимых решений.
Из рис. 10 следует, что двойственная задача не имеет планов, поскольку многоугольник решений ее пуст. Это означает, что если исходная задача двойственной пары не имеет оптимального плана из-за неограниченности на множестве допустимых решений ее целевой функции, то двойственная задача также не имеет планов.
 Нахождение решения двойственных задач. Рассмотрим пару двойственных задач – основную задачу линейного программирования (43) – (45) и двойственную к ней задачу (46), (47).
Предположим, что с помощью симплексного метода найден оптимальный план X* задачи (43) – (45) и этот план определяется базисом, образованным векторами
Нахождение решения двойственных задач. Рассмотрим пару двойственных задач – основную задачу линейного программирования (43) – (45) и двойственную к ней задачу (46), (47).
Предположим, что с помощью симплексного метода найден оптимальный план X* задачи (43) – (45) и этот план определяется базисом, образованным векторами 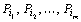 .
Обозначим через .
Обозначим через 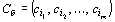 вектор-строку, составленную из коэффициентов при неизвестных в целевой функции (43) задачи (43) – (45), а через вектор-строку, составленную из коэффициентов при неизвестных в целевой функции (43) задачи (43) – (45), а через 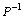 – матрицу, обратную матрице Р,составленной из компонент векторов – матрицу, обратную матрице Р,составленной из компонент векторов 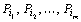 базиса. Тогда имеет место следующее утверждение.
Теорема 10.
Если основная задача линейного программирования имеет оптимальный план X*, то базиса. Тогда имеет место следующее утверждение.
Теорема 10.
Если основная задача линейного программирования имеет оптимальный план X*, то 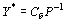 является оптимальным планом двойственной задачи.
Таким образом, если найти симплексным методом оптимальный план задачи (43) – (45), то, используя последнююсимплекс–таблицу, можно определить является оптимальным планом двойственной задачи.
Таким образом, если найти симплексным методом оптимальный план задачи (43) – (45), то, используя последнююсимплекс–таблицу, можно определить 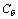 и и 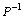 и с помощью соотношения и с помощью соотношения 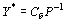 найти оптимальный план двойственной задачи (46), (47).
В том случае, когда среди векторов найти оптимальный план двойственной задачи (46), (47).
В том случае, когда среди векторов 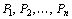 , составленных из коэффициентов при неизвестных в системе уравнений (44), имеется т единичных, указанную матрицу , составленных из коэффициентов при неизвестных в системе уравнений (44), имеется т единичных, указанную матрицу 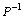 образуют числа первых т строк последней симплекс–таблицы, стоящие в столбцах данных векторов. Тогда нет необходимости определять оптимальный план двойственной задачи умножением образуют числа первых т строк последней симплекс–таблицы, стоящие в столбцах данных векторов. Тогда нет необходимости определять оптимальный план двойственной задачи умножением 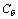 на на 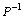 , поскольку компоненты этого плана совпадают с соответствующими элементами (m +1)–й строки столбцов единичных векторов, если данный коэффициент , поскольку компоненты этого плана совпадают с соответствующими элементами (m +1)–й строки столбцов единичных векторов, если данный коэффициент 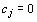 , и равны сумме соответствующего элемента этой строки и , и равны сумме соответствующего элемента этой строки и 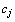 если если 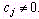 Сказанное выше имеет место и для симметричной пары двойственных задач. При этом так как система ограничений исходной задачи содержит неравенства вида “
Сказанное выше имеет место и для симметричной пары двойственных задач. При этом так как система ограничений исходной задачи содержит неравенства вида “ 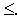 ”, то компоненты оптимального плана двойственной задачи совпадают с соответствующими числами (m +1)–й строки последней симплекс–таблицы решения исходной задачи. Указанные числа стоят в столбцах векторов, соответствующих дополнительным переменным.
Пример 15.
Для задачи, состоящей в определении максимального значения функции ”, то компоненты оптимального плана двойственной задачи совпадают с соответствующими числами (m +1)–й строки последней симплекс–таблицы решения исходной задачи. Указанные числа стоят в столбцах векторов, соответствующих дополнительным переменным.
Пример 15.
Для задачи, состоящей в определении максимального значения функции 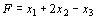 при условиях при условиях
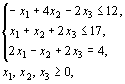 составить двойственную задачу и найти ее решение.
Решение. Двойственная задача по отношению к исходной состоит в нахождении минимума функции
составить двойственную задачу и найти ее решение.
Решение. Двойственная задача по отношению к исходной состоит в нахождении минимума функции 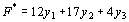 при условиях при условиях
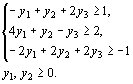 Чтобы найти решение двойственной задачи, сначала находим решение исходной задачи методом искусственного базиса. Оно приведено в таблице 12.
Из последней симплекс-таблицы видно, что двойственная задача имеет решение
Чтобы найти решение двойственной задачи, сначала находим решение исходной задачи методом искусственного базиса. Оно приведено в таблице 12.
Из последней симплекс-таблицы видно, что двойственная задача имеет решение 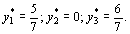 Оптимальные двойственные оценки удовлетворяют всем условиям двойственной задачи. При этом минимальное значение целевой функции двойственной задачи, равное
Оптимальные двойственные оценки удовлетворяют всем условиям двойственной задачи. При этом минимальное значение целевой функции двойственной задачи, равное 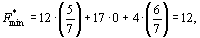 совпадает с максимальным значением целевой функции совпадает с максимальным значением целевой функции 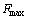 исходной задачи.
Таблица 12 исходной задачи.
Таблица 12
Экономическая интерпретация двойственных задач. Экономическую интерпретацию двойственных задач и двойственных оценок рассмотрим на примере. |
 2015-08-21
2015-08-21 429
429







