101. Пассажир электропоезда, движущегося со скоростью 15 м/с, заметил, что встречный поезд длиной 210 м прошел мимо него за 6,0 с. Определить скорость встречного поезда.
102. При неподвижном эскалаторе метрополитена пассажир поднимается за t1=120 с, а по движущемуся при той же скорости относительно ступенек – за
t2=30 с. Определить время подъема пассажира, неподвижно стоящего на движущемся эскалаторе.
103. Определить скорость моторной лодки относительно воды, если при движении по течению реки её скорость 10 м/с, а при движении против течения – 6,0 м/с. Чему равна скорость течения воды в реке?
104. Скорость поезда, при торможении двигающегося равнозамедленно, уменьшается в течение 1 мин от 40 км/ч до 28 км/ч. Найти ускорение поезда и расстояние, пройденное им за время торможения.
105. Движение материальной точки задано уравнением x=at+bt2+ct3, где
a=5 м/с, b=0,2 м/с2, с=0,1 м/с3. Определить скорость точки в момент времени t1=2 с, t2=4 с, а также среднюю скорость в интервале времени от t1 до t2.
106. Скорость материальной точки, движущейся вдоль оси X, определяется уравнением uX = 0,2-0,1t. Найти координату точки в момент времени t=10 с, если в начальный момент времени она находилась в точке x0=1.
107. Самолет для взлета должен иметь скорость 100 м/с. Определить время разбега и ускорение, если длина разбега 600 м; движение самолета при этом считать равноускоренным.
108. Автомобиль движется со скоростью u1=25 м/с. На пути S=40 м производится торможение, после чего скорость уменьшается до u2=15 м/с. Считая движение автомобиля равнозамедленным, найти модуль ускорения и время торможения.
109. Первую половину пути тело двигалось со скоростью u1 = 2 м / с, вторую половину пути - со скоростью u2 = 8 м / с. Определить среднюю скорость движения.
110.Точка прошла половину пути со скоростью 10 км/ч. Оставшуюся часть пути она половину времени двигалась со скоростью 18 км/ч, а последний участок - со скоростью 25,2 км/ч. Найти среднюю скорость движения точки.
111. Определить угловое ускорение маховика, частота вращения которого за время N=20 полных оборотов возросла равномерно от n0=1 об/c до n=5 об/с.
112. Определить зависимость угловой скорости и углового ускорения от времени для твердого тела, вращающегося вокруг неподвижной оси z по закону j=at-bt2, где a=20 рад/с, b=1 рад/с2. Каков характер движения этого тела? Построить графики зависимости угловой скорости и углового ускорения от времени.
113. Колесо радиусом R=10 см вращается с постоянным угловым ускорением e=3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость; 2) линейную скорость; 3) тангенциальное ускорение; 4) нормальное ускорение; 5) полное ускорение.
114. Твёрдое тело вращается вокруг неподвижной оси по закону
j = 6,0 t -2,0 t3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки.
115. Вентилятор вращается с частотой 600 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Какое время прошло с момента выключения вентилятора до его полной остановки?
116. Колесо вращается с угловым ускорением 2 рад/с2. Через время 0,5 с после начала движения полное ускорение точек на ободе колеса равно 0,15 м/с2. Найти радиус колеса.
117. Велосипедное колесо вращается с частотой n=5 c-1 . Под действием сил трения оно остановилось через Dt=1 мин. Определить угловое ускорение и число оборотов, которое сделало колесо за это время.
118. Ось с двумя параллельными бумажными дисками, расположенными на расстоянии 0,5 м друг от друга, вращается с частотой 1200 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; пробоины в дисках смещены друг относительно друга на угол 15о. Найти скорость пули. Силой тяжести, действующей на пулю пренебречь.
119. Движение точки по окружности радиусом 4 м задано уравнением
S = 10 - 2 t + t2. Найти тангенциальное, нормальное и полное ускорения точки в момент времени 2 с.
120. Точка движется по окружности радиусом 2 м согласно уравнению S = 2 t3. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Чему будет равно полное ускорение точки в этот момент времени?
121. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a=45°. Зависимость пройденного телом пути S от времени t задана уравнением S=Ct2, где С=1,73 м/с2. Найти коэффициент трения k тела о плоскость.
122. Тело массой m=0,5 кг движется так, что зависимость координаты тела от времени t дается уравнением X=Asin(wt), где А=5 см и w=p рад/с. Найти силу F, действующую на тело через время t=(1/6) с после начала движения.
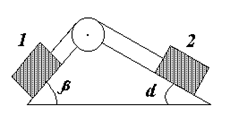 |
123. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы a=30° и b=45°. Гири 1 и 2 одинаковой массы m1=m2=1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
124. Самолёт делает «мёртвую петлю» радиусом 500 м с постоянной скоростью 360 км/ч. Найти вес летчика массой 70 кг в нижней, верхней и средней точках петли.
125. К пружинным весам подвешен блок. Через блок перекинули шнур, к концам которого привязали грузы массой 1,5 кг и 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.
126. Наклонная плоскость, образующая угол 25о с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения тела о плоскость.
127. На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью:
а) в гору с уклоном 1 м на каждые 25 м пути; б) под гору с тем же уклоном.
128. На столе стоит тележка массой m1=4 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением будет двигаться тележка, если к другому концу шнура привязать гирю массой m2=1 кг?
129. Аэростат массой m начал опускаться с постоянным ускорением а. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.
130. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол 15о с горизонтом. Найти коэффициент трения, если время подъёма тела оказалось в 2 раза меньше времени спуска.
131. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого J=50 кг×м2 и радиус R=20 см. Момент сил трения вращающегося блока MТР=98,1 Н×м. Найти разность сил натяжения нити Т1-Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением
e=2,36 рад/с. Блок считать однородным диском.
132. На барабан массой m0=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение a груза. Барабан считать однородным цилиндром. Трением пренебречь.
133. Маховик радиусом R=0,2 м и массой m=10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения,
Т=14,7 Н. Какую частоту вращения будет иметь маховик через время t=10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
134. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени даётся уравнением w = А + 8 t, где А=const. Найти касательную силу, приложенную в ободу диска. Трением пренебречь.
135. Маховое колесо, момент инерции которого 245 кг×м2, вращается с частотой 20 об / с. Через 1 минуту после того, как на колесо перестал действовать момент сил, оно остановилось. Найти момент сил трения и число оборотов, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
136. Однородный стержень длиною 1м и весом 0,5 Н вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент равен 9,8 × 10-2 Н×м?
137. Автомобиль идет по закруглению шоссе, радиус кривизны которого равен 200 м. Коэффициент трения колес о покрытие дороги равен 0,1. При какой скорости автомобиля начнется его занос?
138. Однородный диск радиусом R=0,2м и массой 0,5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением w=A+Bt, где 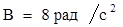 . Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.
. Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.
139. Найти момент импульса земного шара относительно оси вращения.
140. Грузик, привязанный к шнуру длиной L=50см, описывает окружность в горизонтальной плоскости. Какой угол (в градусах) образует шнур с вертикалью, если частота вращения n=1c-1?
141. Под действием постоянной силы вагонетка прошла путь 5 м и приобрела скорость 2 м / с. Определить работу силы, если масса вагонетки 400 кг и коэффициент трения равен 0,01.
142. Вычислить работу, совершаемую при равноускоренном подъёме груза массой 100 кг на высоту 4 м за время 2 с.
143. На тело, двигавшееся со скоростью 2 м/с, подействовала сила 2 Н в направлении скорости. Через 10 с после начала действия силы кинетическая энергия тела оказалась равной 100 Дж. Найти массу тела, считая его материальной точкой.
144. Найти работу, которую надо совершить, чтобы увеличить скорость движения тела от 2 м/с до 6 м/с на пути в 10 м. На всём пути действует постоянная сила трения, равная 2 Н. Масса тела равна 1 кг.
145. Найти, какую мощность развивает двигатель автомобиля массой в
1000 кг, если известно, что автомобиль едет с постоянной скоростью 36 км / ч:
1) по горизонтальной дороге, 2) в гору с уклоном 5 м на каждые 100 м пути, 3) под гору с тем же уклоном. Коэффициент трения 0,07.
146. Маховик вращается по закону, выражаемому уравнением
j = 2+16t-2t2. Момент инерции маховика равен 50 кг×м2. Найти закон, по которому меняется вращающий момент сил и мощность. Чему равна мощность в момент времени 3 с?
147. Якорь мотора вращается с частотой 1500 об/мин. Определить вращающий момент сил, если мотор развивает мощность 500 Вт.
148. Ремённая передача передаёт мощность 9 кВт. Шкив передачи имеет диаметр 0,48 м и вращается с частотой 240 об/мин. Натяжение ведущей ветви ремня в два раза больше натяжения ведомой ветви. Найти натяжение обеих ветвей ремня.
149. Диск массой 1 кг и диаметром 0,6 м вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с. Какую работу надо совершить, чтобы остановить диск?
150. Камень, пущенный по поверхности льда со скоростью u=2м/с, прошел до полной остановки расстояние S=20,4 м. Найти коэффициент трения камня по льду, считая его постоянным.
151. Человек, весом 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку весом 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка? С какой скоростью будет двигаться тележка, если человек бежал ей навстречу?
152. Пуля, летящая горизонтально со скоростью u = 400 м/c, попадает в брусок, подвешенный на нити длиной L = 4м, и застревает в нем. Определить угол a, на который отклонится брусок, если масса пули m1 = 20 г, а бруска m2 = 5кг.
153. Шар массой 1 кг, катящийся без скольжения, ударяется о стенку, откатывается от неё. Скорость шара до удара 10 см/с, после удара 8 см/с. Найти количество тепла, выделившееся при ударе.
154. Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. Найти, на какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения коньков о лед равен 0,02.
155. Тело массой 2 кг движется навстречу второму телу массой 1,5 кг и неупруго сталкивается с ним. Скорости тел перед столкновением 1 м/с и 2 м/с соответственно. Сколько времени будут двигаться эти тела после столкновения, если коэффициент трения равен 0,1.
156. Шарик массой 200 г ударился о стенку со скоростью 10 м/с и отскочил от неё с такой же по модулю скоростью. Определить импульс, полученный стенкой, если до удара шарик двигался под углом 30° к плоскости стенки.
157. Два шарика массами 2 и 4 кг двигаются со скоростями 5 м/с и 7 м/с соответственно. Определить скорость шаров после прямого неупругого удара, если большой шар догоняет меньший.
158. Абсолютно упругий шар массой 1,8 кг сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36 % своей кинетической энергии. Определить массу большего шара.
159. Стержень длиной L = 1,5 м и массой M = 10 кг может вращаться вокруг неподвижной оси, проходящий через верхний конец стержня. В середину стержня ударяет пуля массой m= 10 г, летящая в горизонтальном направлении со скоростью u0 = 500 м/c, и застревает в стержне. На какой угол a отклонится стержень после удара?
160. На покоящийся шар массой М = 1 кг, подвешенный на длинном жестком стержне, попадает пуля m = 10 г. Угол между направлением полета пули и линией стержня a = 45°. Удар центральный. После удара пуля застревает в шаре и шар вместе с пулей, отклонившись, поднимается на высоту h= 0,12 м относительно первоначального положения. Найти скорость u пули. Массой стержня пренебречь.
161. Молотком, масса которого М = 1 кг, забивают в стену гвоздь массой
m = 50г. Определить КПД удара молотка.
162. К ободу диска массой m=5 кг приложена постоянная касательная сила F=2 Н. Какую кинетическую энергию будет иметь диск через t=5 с после начала действия силы?
163. На краю горизонтальной платформы, имеющей форму диска радиусом
2 м, стоит человек. Масса платформы 200 кг, масса человека 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль её края со скоростью 2 м/с относительно платформы.
164. Платформа, имеющая форму диска, может вращаться вокруг вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы с постоянной скоростью и, обойдя её, вернется в исходную точку? Масса платформы 240 кг, масса человека 60 кг. Момент инерции человека рассчитывать как для материальной точки.
165. Какую работу совершит человек, если он от края вращающейся платформы перейдет в её центр? Масса платформы 100 кг, масса человека 80 кг, первоначальная частота вращения 10 об/мин, радиус платформы 2 м.
166. Диск радиусом 20 см и массой 5 кг вращался, делая 8 об/с. При торможении он остановился через 4 секунды. Определить тормозящий момент.
167. Маховик вращается с частотой n=10 об/с. Его кинетическая энергия WК=7,85 кДж. За какое время t момент сил М=50 Н×м, приложенный к маховику, увеличит угловую скорость маховика вдвое?
168. Вентилятор вращается с частотой n = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Работа сил торможения А = 44,4 Дж. Найти момент инерции J вентилятора и момент сил торможения М.
169. Маховое колесо начинает вращаться с угловым ускорением e=0,5 рад/с2 и через время t1=15 с после начала движения приобретает момент импульса
L=73,5 (кг×м2)/с. Найти кинетическую энергию WК колеса через время t2=20 с после начала движения.
170. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути.
171. Найти релятивистское сокращение размеров протона, кинетическая энергия которого 10 ГэВ.
172. Какую работу необходимо совершить, чтобы увеличить скорость частицы с массой покоя m0 от 0,6 с до 0,8 с?
173. Солнце ежеминутно испускает энергию, равную 6,5×1021 кВт×ч. Считая излучение солнца постоянным, найти, за какое время масса Солнца уменьшится в
2 раза.
174. Частица движется со скоростью u=0,5×с. Во сколько раз масса частицы больше массы покоя?
175. Кинетическая энергия протона 10 МэВ. Определить его импульс.
176. При какой скорости движения релятивистское сокращение длины движущегося тела составляет 25 %.
177. Мезон движется со скоростью 0,96 с. Какой промежуток времени по часам наблюдателя соответствует одной секунде “собственного” времени мезона?
178. C какой скоростью движется частица, если ее масса в 4 раза больше массы покоя?
179. Определить скорость куба, при которой его плотность возрастает в 2 раза.
180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c.
III. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяются два качественно различных метода: статистический и термодинамический. Первый лежит в основе молекулярной физики, второй – термодинамики.
Молекулярная физика – раздел физики, изучающий строение и свойства вещества, исходя из молекулярно–кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном движении.
Термодинамика – раздел физики, изучающий общие свойства макроскопических систем и процессы перехода между различными состояниями.
Состояние системы задается термодинамическими параметрами (параметрами состояния) – совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру Т, давление р, и объем V. Температура тела – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы – одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом.
Параметры состояния системы могут меняться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из термодинамических параметров, называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется.
1. Молекуляро-кинетическая теория идеальных газов
1.2. Опытные законы идеального газа
В молекулярно-кинетической теории пользуются моделью идеального газа, удовлетворяющей следующим условиям: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) потенциальной энергией взаимодействия молекул можно пренебречь; 3) столкновения молекул между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки к идеальному газу. Кроме того, внеся поправки на собственный размер молекул и действующие молекулярные силы, можно перейти к теории реальных газов.
Опытным путем, задолго до появления молекулярно-кинетической теории, был открыт целый ряд законов, описывающих поведение идеальных газов.
Закон Бойля-Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:
pV=const при Т, m=const.
Изотермы представляют собой гиперболы, расположенные на графике тем выше, чем выше температура (рис. 9).
|
|
|
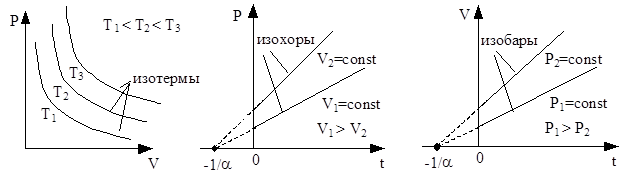
Законы Гей-Люссака: 1) давление данной массы газа при постоянном объеме изменяется линейно с температурой:
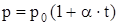 при V, m=const (рис. 10);
при V, m=const (рис. 10);
2) объем данной массы газа при постоянном давлении изменяется линейно с температурой:
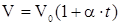 при p, m=const (рис. 11).
при p, m=const (рис. 11).
В этих уравнениях t – температура по шкале Цельсия, p0 и V0 – давление и объем при 0° C, a - температурный коэффициент. Изобары и изохоры пересекают ось температур в точке t = - 1/a, (рис. 10 и11), определяемой из условия
1 + a t = 0. Если сместить начало отсчета в эту точку, то происходит переход к шкале Кельвина, откуда 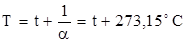 . Законам Гей-Люссака можно придать более удобный вид, вводя в формулы термодинамическую температуру
. Законам Гей-Люссака можно придать более удобный вид, вводя в формулы термодинамическую температуру
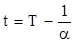 :
:
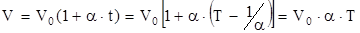 ,
,
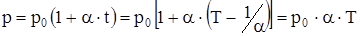 ,
,
или
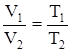 при p, m=const;
при p, m=const;
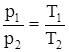 при V, m=const, где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
при V, m=const, где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях p = 1,013×105 Па;
Т=273,15 К; этот объем V=22,41×10-3 м3/моль.
По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро: NA=6,022×1023 моль-1.
Закон Дальтона: давление смеси нормальных газов равно сумме парциальных давлений входящих в нее газов, т.е. p = p1 + p2 + p3 +¼, где р1, р2 …- парциальные давления – давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
1.2. Уравнение Менделеева–Клапейрона
Состояние некоторой массы газы определяется тремя термодинамическими параметрами: давлением p, объемом V, температурой T. Между этими параметрами существует связь, показываемая уравнением состояния f (p,V,T)=0, где каждая переменная является функцией двух других. Французский физик и инженер Б. Клапейрон (1799-1864) вывел уравнение состояния идеального газа, объединив законы Бойля–Мариотта и Гей–Люссака.
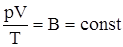 , где B – газовая постоянная, различная для разных газов.
, где B – газовая постоянная, различная для разных газов.
Д.И. Менделеев (1834-1907) объединил уравнение Клапейрона и закон Авогадро, отнеся уравнение Клапейрона к одному молю газа: 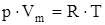 . При одинаковых p и T моли всех газов занимают одинаковый объем Vm, поэтому постоянная B будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. R=8,31
. При одинаковых p и T моли всех газов занимают одинаковый объем Vm, поэтому постоянная B будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. R=8,31 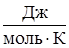 . Если один моль газа занимает объем Vm, то при тех же условиях масса m газа займет объем
. Если один моль газа занимает объем Vm, то при тех же условиях масса m газа займет объем 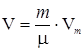 , где m - молярная масса газа.
, где m - молярная масса газа.
Уравнение Менделеева–Клапейрона для массы m газа 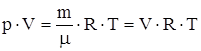 , где
, где 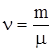 - число молей.
- число молей.
1.3. Основное уравнение молекулярно-кинетической теории газов
Основное уравнение молекулярно-кинетической теории устанавливает зависимость между давлением и объемом газа и кинетической энергией поступательного движения его молекул: 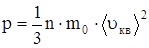 ,
,
где p – давление газа, оказываемое им на стенки сосуда; n – концентрация молекул газа; m0 – масса молекулы газа; <u 2КВ> - средняя квадратичная скорость молекул.
Если газ в объеме V содержит N молекул, движущихся со скоростями
u1, u1, u1,…, uN, то средняя квадратичная скорость характеризует всю совокупность молекул газа и определяется из соотношения
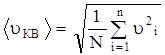 .
.
Учитывая, что 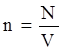 , получим
, получим
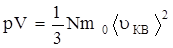 , (1)
, (1)
или
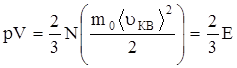 , (2)
, (2)
где E – суммарная кинетическая энергия поступательного движения всех молекул. Таким образом, мы получим уравнение (2) эквивалентное уравнение (1).
Используя уравнение Менделеева–Клапейрона, можно показать, что
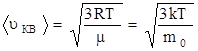 ,
,
где k – постоянная Больцмана, k = 1,38 × 10-23 Дж/К. Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
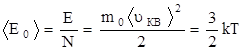
пропорциональна термодинамической температуре и зависит только от нее.
1.4. Закон Максвелла для распределения молекул идеального газа
по скоростям теплового движения
По молекулярно-кинетической теории, как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m0 в газе, находящемся в состоянии теплового равновесия при Т=cоnst, остается постоянной и 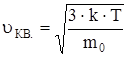 . Это объясняется тем, что в газе, находящемся в состоянии теплового равновесия, установлено некоторое стационарное распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Максвеллом.
. Это объясняется тем, что в газе, находящемся в состоянии теплового равновесия, установлено некоторое стационарное распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Максвеллом.
Закон Максвелла описывается некоторой функцией f(u), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные du, то на каждый интервал скорости будет приходиться некоторое число молекул dN(u), имеющих скорости в интервале (u+du).
 и
и 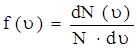 , где N – число молекул газа.
, где N – число молекул газа.
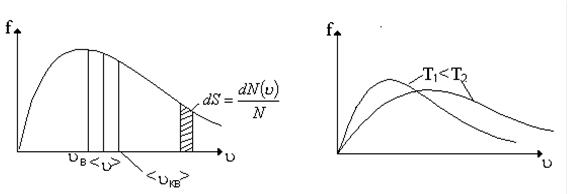
рис.12 рис. 13
Таким образом, функция f(u) определяет относительное число молекул 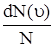 , скорости которых лежат в интервале от u до (u+du).
, скорости которых лежат в интервале от u до (u+du).
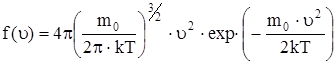 . (3)
. (3)
График функции распределения приведен на рис. 12. Из приведенного графика следует, что функция распределения стремится к нулю при u®0 и u®¥ и проходит через максимум при некоторой скорости uВ, называемой наиболее вероятной скоростью. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно uВ.
Значение наиболее вероятной скорости можно найти, продифференцировав уравнение Максвелла (3) по аргументу u и приравняв результат нулю, используя условие для максимума выражения f(u):
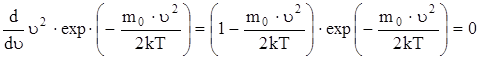 ;
;
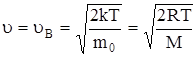 .
.
На рис. 13 показано смещение uВ с изменением температуры. Получим среднюю скорость 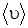 . Среднее значение любой величины находят, умножая каждое возможное значение этой величины на число молекул, обладающих этим значением данной величины, а затем полученные числа суммируют и делят на N.
. Среднее значение любой величины находят, умножая каждое возможное значение этой величины на число молекул, обладающих этим значением данной величины, а затем полученные числа суммируют и делят на N.
Так как распределение молекул непрерывно, вместо суммы мы имеем интеграл
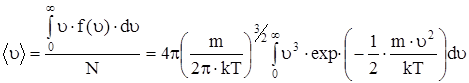 ;
;
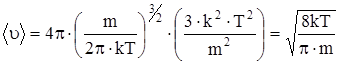 .
.
При выводе основного уравнения молекулярно-кинетической теории и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул - с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает (рис. 14).
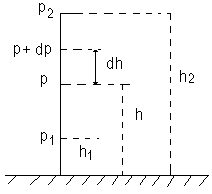
Рис. 14
При h=0 p1=p0, где p0 - нормальное давление на уровне моря.
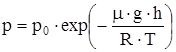
На рис.15 показано изменение давления газа с высотой для различных газов при T = const, а на рис. 16 – изменение давления газа (m = const) при разных температурах.
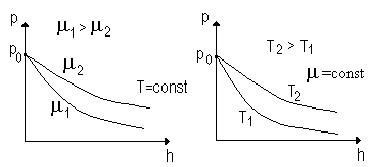 |
Рис. 15 Рис. 16
Барометрическую формулу можно преобразовать, если воспользоваться выражением 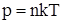 :
: 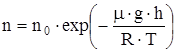 , где n0 - концентрация молекул газа на высоте h = 0, n – на высоте h. Так как
, где n0 - концентрация молекул газа на высоте h = 0, n – на высоте h. Так как 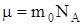 , а
, а 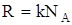 , то
, то
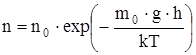
и 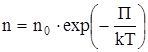 - распределение Больцмана во внешнем потенциальном поле,
- распределение Больцмана во внешнем потенциальном поле,
где П=m0×g×h – потенциальная энергия молекулы в поле тяготения.
1.6. Среднее число столкновений и средняя длина свободного пробега молекул
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь L, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, то можно говорить о средней длине свободного пробега молекул < L>.
Минимальное расстояние, на которое сближаются центры молекул, называется эффективным диаметром молекулы d. Он зависит от скорости сталкивающихся молекул, т.е. от температуры. За 1 с молекула проходит путь, равный <u>, и если <z> - среднее число столкновений за единицу времени, то 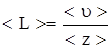 .
.
Молекула, которая движется по центру цилиндра (рис. 17), сталкивается только с теми молекулами, центры которых находятся внутри цилиндра радиусом 2r.
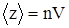 ,
,
где n – концентрация молекул, 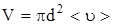 , (<u> - средняя скорость молекул).
, (<u> - средняя скорость молекул).
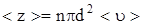 ,
,
более точно 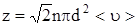 - при учете движения других молекул.
- при учете движения других молекул.
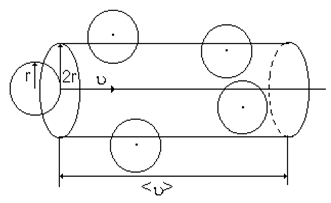
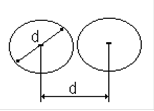
Рис. 17
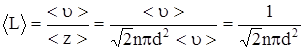 .
.
1.7. Явления переноса в термодинамически неравновесных системах
В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), количества движения (внутреннее трение).
Теплопроводность
Если в одной области газа средняя кинетическая энергия молекул больше чем в другой, то с течением времени вследствие постоянных столкновений молекул температура выравнивается. Процесс передачи энергии в форме тепла подчиняется закону теплопроводности Фурье: количество теплоты q, которое переносится за единицу времени, через единичную площадку, прямо пропорционально 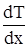 - градиенту температуры, равному скорости изменения температуры на единицу длины x в направлении нормали к этой площади.
- градиенту температуры, равному скорости изменения температуры на единицу длины x в направлении нормали к этой площади.
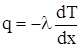 ,
,
где l - теплопроводность. Знак минус показывает, что при теплопроводности энергия переносится в сторону убывания температуры. Теплопроводность равна количеству теплоты, переносимой через единичную площадку в единицу времени при температурном градиенте 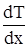 , равном единице. Очевидно, что теплота, прошедшая посредством теплопроводности через площадь S за время t:
, равном единице. Очевидно, что теплота, прошедшая посредством теплопроводности через площадь S за время t:
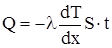 Можно показать, что
Можно показать, что 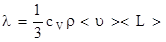 , где cv – удельная теплоемкость газа при постоянном объеме, r - плотность газа.
, где cv – удельная теплоемкость газа при постоянном объеме, r - плотность газа.
Диффузия
Если в стакан с водой аккуратно влить пищевой краситель, то мы увидим, что вода будет постепенно окрашиваться. Это смешивание обусловлено хаотическим движением молекул и называется диффузией.
Диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности.
Перенос массы вещества подчиняется закону Фика: масса вещества m переносимая за единицу времени через единичную площадку, прямо пропорциональна градиенту плотности:
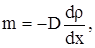
где D – диффузия (коэффициент диффузии). Знак минус показывает, что перенос массы происходит в направлении убывания плотности.
Диффузия D равна массе вещества, переносимого через единицу площади за единицу времени при градиенте плотности 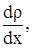 равном единице. Масса Мвещества, перенесенная в результате диффузии через площадь S за время t:
равном единице. Масса Мвещества, перенесенная в результате диффузии через площадь S за время t:
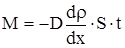 .
.
Согласно кинетической теории газов,
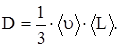
Внутреннее трение (вязкость)
Механизм возникновения внутреннего трения между слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего количество движения слоя, движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Внутреннее трение подчиняется закону Ньютона:
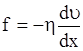 ,
,
где f – сила внутреннего трения, действующая на единицу площади поверхности слоя, h - динамическая вязкость (вязкость), 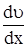 - градиент скорости. Знак минус указывает, что сила трения направлена против скорости. Вязкость h вычисляется по формуле:
- градиент скорости. Знак минус указывает, что сила трения направлена против скорости. Вязкость h вычисляется по формуле:
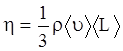 .
.
Сила F, действующая на площадь S, пропорциональна этой площади и градиенту скорости 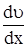 :
:
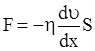 .
.
Между l, h и Dсуществуют простые закономерности:
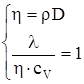
2.1. Внутренняя энергия
Внутренняя энергия U – энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, и. т. д.) и энергия взаимодействия частиц.
Молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения.
В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек - атомов, жестко связанных недеформируемой связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Трехатомная и многоатомные нелинейные молекулы имеют шесть степеней свободы – три поступательные и три вращательные.
На каждую поступательную степень свободы приходится энергия 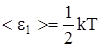 . Столько же приходится на вращательную степень.
. Столько же приходится на вращательную степень.
Таким образом, средняя кинетическая энергия молекулы идеального газа 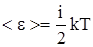 , где i – сумма числа поступательных и вращательных степеней свободы молекулы
, где i – сумма числа поступательных и вращательных степеней свободы молекулы 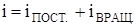
Внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий NA молекул: 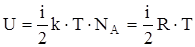 . Если имеем nмолей газа, то его внутренняя энергия:
. Если имеем nмолей газа, то его внутренняя энергия: 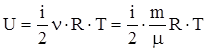 .
.
2.2. Первое начало термодинамики
Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия.
Внутренняя энергия системы может измениться за счет совершения работы над системой и сообщения ей количества теплоты.
Передача теплоты может осуществляться тремя способами:
1) теплопроводностью 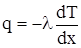 ;
;
2) конвекцией, где происходит перенос теплого вещества к холодному;
3) излучением.
Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и перешла в новое состояние U2, совершив при этом работу А против внешних сил.
Q считается положительным, если оно подводится к системе, а работа - положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии DU=U2-U1 будет одинаковым и равным разности между количеством теплоты, полученным системой и работой, совершаемой системой против внешних сил:
DU = Q-A, или Q= DU+A – математическое выражение первого начала термодинамики: теплота, сообщаемая системе, расходуется на увеличение ее внутренней энергии и на совершение ею работы против внешних сил. Q выражается в тех же единицах, что и работа, и внутренняя энергия, т.е. в джоулях (Дж).
Если система периодически возвращается в первоначальное состояние, то DU=0 и A=Q, нельзя построить вечный двигатель, который совершал бы большую по величине работу, чем количество сообщенной ему извне энергии.
2.3. Работа газа при изменении его объема
Найдем в общем виде работу, совершаемую газом при изменении его объема.
Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде (рис. 18).
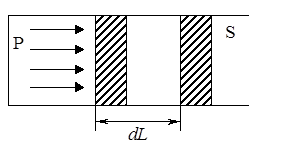
Рис. 18
Если газ, расширяясь, передвигает поршень на расстояние 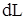 , то он производит над ним работу:
, то он производит над ним работу:
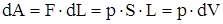 ,
,
где S - площадь поршня, sdL = dV - изменение объема системы. Таким образом, 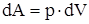 . Полную работу А, совершаемую газом при изменении его объема от V1 до V2, найдем путем интегрирования:
. Полную работу А, совершаемую газом при изменении его объема от V1 до V2, найдем путем интегрирования:
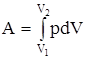 .
.
Результат интегрирования определяется характером зависимости между давлением и объемом газа.
2.4. Теплоемкость
Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1К: 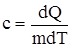 ([c] = 1 Дж/(кг× К)). Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:
([c] = 1 Дж/(кг× К)). Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К: 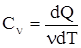 , где
, где 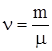 - количество молей вещества ([Cn] = 1 Дж/(моль × К)). Удельная теплоемкость связана с молярной соотношением
- количество молей вещества ([Cn] = 1 Дж/(моль × К)). Удельная теплоемкость связана с молярной соотношением
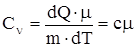 .
.
Различают теплоемкости при постоянном давлении и постоянном объеме, если в процессе нагревания вещества поддерживаются постоянным соответственно давление и объем.
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщенная газу извне теплота идет на увеличение его внутренней энергии:
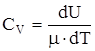 , то есть молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии газа при повышении его температуры на 1 К.
, то есть молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии газа при повышении его температуры на 1 К.
Так как 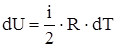 , то
, то 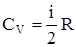 .
.
Используя первое начало термодинамики можно показать, что молярная теплоемкость газа при постоянном объеме CVи молярная теплоемкость газа при постоянном давлении CPсвязаны соотношением: 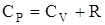 . Это выражение называется уравнением Майера. Тогда
. Это выражение называется уравнением Майера. Тогда 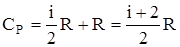 .
.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение CP к CV:
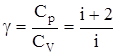 .
.
Из последних формул следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры.
2.5. Применение первого начала термодинамики к изопроцессам
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из параметров остается постоянным.
Изохорный процесс. (V = const). При изохорном процессе газ не совершает работу над внешними силами 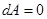 . Из первого начала термодинамики следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
. Из первого начала термодинамики следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
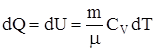 .
.
Изобарный процесс (p = const). Диаграмма этого процесса в координатах p, V изображается прямой 1-2, параллельной оси V (рис. 19). При изображенном процессе работа газа при расширении от объеме V1 до V2 равна: 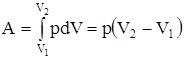 и определяется площадью заштрихованного прямоугольника на рис. 19.
и определяется площадью заштрихованного прямоугольника на рис. 19.
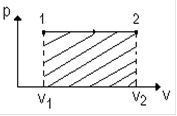 |
Рис. 19
Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то 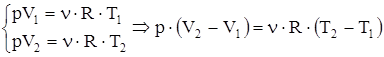 . Тогда выражение для работы изобарного расширения примет вид
. Тогда выражение для работы изобарного расширения примет вид 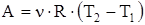 . Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-Т1 = 1 К, то для одного моля газа R=A, то есть R численно равна работе расширения одного моля идеального газа при нагревании его на 1К.
. Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-Т1 = 1 К, то для одного моля газа R=A, то есть R численно равна работе расширения одного моля идеального газа при нагревании его на 1К.
В изображенном процессе при сообщении газу количества теплоты 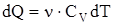 его внутренняя энергия возрастает на величину
его внутренняя энергия возрастает на величину 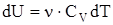 .
.
Изотермический процесс (T = const).
Уравнением изотермического процесса является закон Бойля-Мариотта: pV=const. Найдем работу газа при изотермическом процессе:
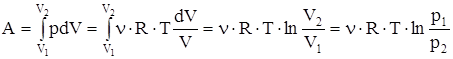 .
.
Из первого начала термодинамики следует, что  и
и 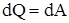 , т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
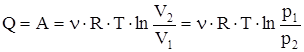 .
.
Адиабатическим называется процесс, при котором отсутствует теплообмен
(dQ = 0) между физической системой и окружающей средой. Близкими к адиабатическим являются все быстропротекающие процессы. Из первого начала термодинамики для адиабатического процесса следует, что 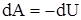 , т.е. работа совершается за счет изменения внутренней энергии системы.
, т.е. работа совершается за счет изменения внутренней энергии системы.
Легко показать, что для адиабатического процесса имеют место равенства
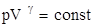 ;
; 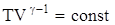 и
и 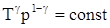 .
.
Эти выражения представляют собой уравнения адиабатического процесса. Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение в виде 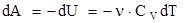 . Если газ адиабатически расширяется от объема V1 до V2, то его температура падает от T1 до T2 и работа расширения идеального газа
. Если газ адиабатически расширяется от объема V1 до V2, то его температура падает от T1 до T2 и работа расширения идеального газа 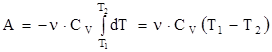 .
.
Это выражение для работы при адиабатическом процессе можно преобразовать к виду
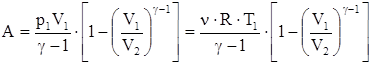 .
.
2.7. Круговой процесс (цикл). Обратимые и необратимые процессы
Круговым процессом или циклом называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 20)
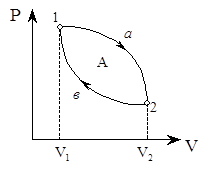
Рис. 20
Площадь фигуры V11a2V2V1 – работа расширения. Площадь фигуры V11в2V2V1 – работа сжатия. Общая работа А определяется площадью кривой 1а2в1.
Если за цикл совершается А>0, то цикл называется прямым, и если А<0, – обратным.
Прямой цикл используется в тепловом двигателе – периодически действующем двигателе, совершающем работу за счет получения извне теплоты.
Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.
В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю (DU=0), тогда 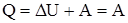 , то есть работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может как получать теплоту, так и отдавать, поэтому
, то есть работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может как получать теплоту, так и отдавать, поэтому 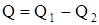 , где Q1 –теплота, полученная системой, а Q2 – отданная.
, где Q1 –теплота, полученная системой, а Q2 – отданная.
Термический коэффициент полезного действия 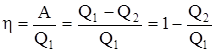 .
.
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и обратном направлении, причем такой процесс происходит сначала в прямом, а затем в обратном направлении, и система возвращается в исходное состояние, а в окружающей среде и в самой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Реальные процессы сопровождаются диссипацией энергии (трение, теплопроводность и т.д.).
Обратимый процесс – это в какой-то степени идеализация реальных процессов. Их рассмотрение важно по двум причинам: 1) многие процессы в природе и технике обратимы; 2) обратимый процесс является наиболее экономичным и приводит к максимальному значению термического коэффициента полезного действия, что позволяет указать пути повышения
КПД реальных тепловых двигателей.
2.8. Второе начало термодинамики
Для описания термодинамических процессов перового начала термодинамики недостаточно. Выражая закон сохранения и превращения энергии, первое начало термодинамики не позволяет определить направление протекания процессов в природе.
Рассмотрим схему теплового двигателя (рис. 21). От термостата с более высокой температурой T1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой T2, называемому холодильником, за цикл передается количество теплоты Q2 и совершается работа A = Q1 - Q2 .
Для того чтобы термический коэффициент полезного действия тепловой машины h=1, необходимо, чтобы Q2= 0, т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Невозможность создания теплового двигателя, работающего только с одним источником теплоты (вечный двигатель второго рода), составляет содержание второго начала термодинамики в формулировке Кельвина–Планка: 1) вечный двигатель второго рода невозможен; 2) невозможен процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

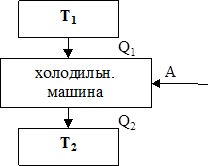
Рис. 21 Рис. 22
Процесс, обратный рассмотренному в тепловом двигателе, используется в холодильной машин, принцип действия которой представлен на рис. 22
Системой за цикл поглощается при низкой температуре T2 количество теплоты Q2 и отдается при более высокой температуре T1 количество теплоты Q1. Для кругового процесса Q = A, но по условию Q = Q1 - Q2 < 0, поэтому A < 0 и
Q2 - Q1 = -A или Q1= Q2 + A, т.е. количество теплоты Q1, отданное системой источнику теплоты при более высокой температуре Т1, больше количества теплоты Q2, полученного при более низкой температуре Т2 на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать более нагретому телу.
Это утверждение составляет содержание второго начала термодинамики в формулировке Клаузиуса: теплота никогда не может переходить сама собой от тел с более низкой температурой к телам с более высокой температурой.
2.9. Цикл Карно и его КПД для идеального газа
Основываясь на втором начале термодинамики, Карно вывел теорему, носящую его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателя и холодильника, наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машин.
Цикл Карно является самым экономичным и состоит из двух изотерм и двух адиабат (рис. 23).
 Рис. 23 Рис. 23 | 1-2 ® расширение и 3-4® сжатие – изотермы 2-3® расширение и 4-1® сжатие – адиабаты. При изотермическом процессе 1-2 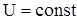 , поэтому , поэтому 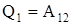 . . 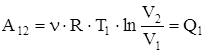 . При адиабатическом расширении 2-3 . При адиабатическом расширении 2-3 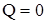 и работа расширения А23 совершается за счет изменения внутренней энергии и работа расширения А23 совершается за счет изменения внутренней энергии |
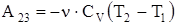 .
.
Теплота Q2, отданная газом холодильнику при изотермическом сжатии, равна работе сжатия А34 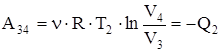 .
.
Работа адиабатического сжатия 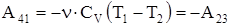 ,
, 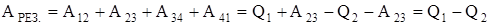 .
.
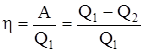 .
.
Применим для адиабат 2-3 и 4-1 известные соотношения 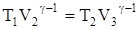 и
и 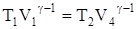 , откуда
, откуда 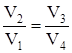 . Таким образом,
. Таким образом,
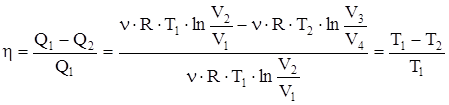 , т.е. для цикла Карно КПД определяется только температурой нагревателя и холодильника.
, т.е. для цикла Карно КПД определяется только температурой нагревателя и холодильника.
Сравнив левую и правую части последней формулы 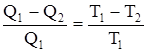 , получим
, получим 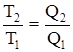 , то есть отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному количеству теплоты.
, то есть отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному количеству теплоты.
Из равенства видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному количеству теплоты.
2.10. Энтропия
Из выражения для обратимого цикла Карно следует, что 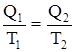 или
или 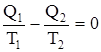 , где Q2 количество теплоты, отдаваемое рабочим телом холодильнику, поэтому оно отрицательно. Следовательно,
, где Q2 количество теплоты, отдаваемое рабочим телом холодильнику, поэтому оно отрицательно. Следовательно, 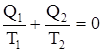 . Величина
. Величина 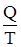 называется приведенным количеством теплоты.
называется приведенным количеством теплоты.
Для цикла Карно алгебраическая сумма приведенных количеств теплоты равна нулю. Приведенное количество теплоты на бесконечно малом участке процесса равно 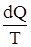 .
.
Для любого обратимого кругового процесса сумма приведенных количеств теплоты равна нулю. Тогда в общем виде может быть записано: 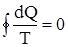 .
.
Из равенства нулю данного интеграла следует, что 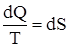 - полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Эта функция называется энтропией S. Для обратимых круговых процессов DS=0. В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: DS>0. DS=0 – это относится только к замкнутым системам. В общем случае DS³0, т.е. S может либо возрастать, либо быть равной нулю.
- полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Эта функция называется энтропией S. Для обратимых круговых процессов DS=0. В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: DS>0. DS=0 – это относится только к замкнутым системам. В общем случае DS³0, т.е. S может либо возрастать, либо быть равной нулю.
Если система совершает равновесный переход их состояния 1 в состояние 2, то 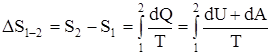 , т.к.
, т.к. 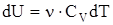 , а
, а 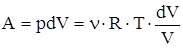 ,
,
то 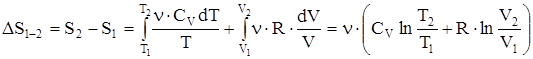 , т.е. изменение энтропии DS1®2 идеального газа не зависит от вида процесса перехода 1®2. При изотермическом процессе (T1 = T2)
, т.е. изменение энтропии DS1®2 идеального газа не зависит от вида процесса перехода 1®2. При изотермическом процессе (T1 = T2) 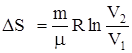 , при изохорном процессе
, при изохорном процессе
(V2 =V1) 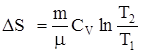 .
.
Так как реальные процессы необратимы, то все процессы в замкнутой системе ведут к увеличению ее энтропии. Этот принцип лежит в основе еще одной формулировки второго начала термодинамики: возможны лишь такие процессы, происходящие в макроскопической системе, которые ведут к увеличению ее энтропии.
Физический смысл энтропии был предложен Больцманом, предположившим, что энтропия связана с термодинамической вероятностью состояния системы. Термодинамическая вероятность состояния системы W – это число способов, которыми может быть реализовано данное состояние макросистемы. 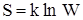 , где k - постоянная Больцмана.
, где k - постоянная Больцмана.
2.11. Реальные газы. Силы и потенциальная энергия взаимодействия
Модель идеального газа, используемая в молекулярно-кинетической теории, позволяет описывать поведение реальных газов при достаточно высоких температурах и низких давлениях. Так, в 1 м3 при нормальных условиях приблизительно 3×1025 молекул, они занимают объем Vмол.»10-4 м3, а при давлении 500 МПа Vмол.=0,5×V.
Ясно, что идеальная модель при высоких давлениях и низких температурах непригодна. При рассмотрении реальных газов надо учитывать силы межмолекулярного взаимодействия.
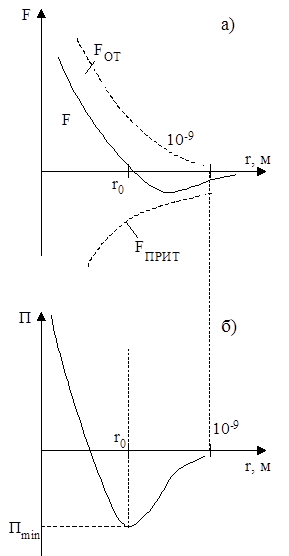 | Они проявляются на расстоянии £ 10-9 м и быстро убывают при увеличении расстояния между молекулами. Между молекулами вещества одновременно действуют силы притяжения FПР и силы отталкивания FОТ. На рис 24а приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами. На расстоянии r = r0 результирующая сила F = 0. Это расстояние соответствует равновесному расстоянию между молекулами. При r < r0 преобладают силы отталкивания. При r > r0 – силы притяжения. При r > 10 |
 2015-09-06
2015-09-06 1539
1539

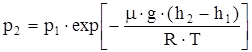 -
- 






