Электростатика. Электрический ток

1. Закон Кулона

,

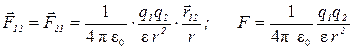где 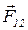- сила, с которой заряд q ₁ действует на заряд q ₂; 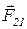- равная ей и противоположно направленная сила; 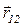- радиус – вектор, направленный от q ₁ к q ₂, а r - модуль 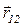; 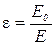- диэлектрическая проницаемость среды; Е ₀ – напряженность электростатического поля в вакууме; Е – напряженность электростатического поля внутри однородного диэлектрика; e ₀ - электрическая постоянная.

2. Напряженность электрического поля и потенциал

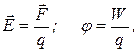
где W_п - потенциальная энергия положительного точечного заряда q, находящегося в данной точке поля.

Сила, действующая на точечный заряд q, находящийся в электрическом поле, и потенциальная энергия этого заряда

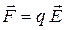; W_п = q j.

3. Напряженность и потенциал поля, создаваемого точечным зарядом q

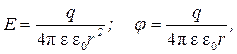
где r - расстояние от заряда q до точки, в которой определяются напряженность или потенциал.

4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции полей).

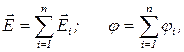
где 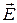_i, j _i - напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.

5. Напряженность и потенциал поля, создаваемого сферой радиусом R на расстоянии r от центра сферы:

а)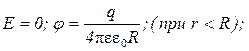

б)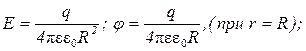

в)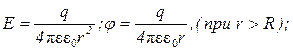

где q - заряд сферы.

6. Линейная плотность заряда: 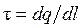или t = q/l.

Поверхностная плотность заряда: 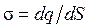или s = q/S.

Объемная плотность заряда: 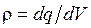или r=q/V.

Связь заряда и плотностей: dq = s dS = t d l= r dV.

7. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длиной dl сзарядом dq = t dl. Такой заряд можно рассматривать как точечный и применять формулы:

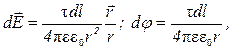
где 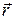- радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность, а r – его модуль.

Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 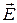и потенциал j поля, создаваемого распределенным зарядом:

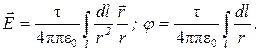
Интегрирование ведется вдоль всей длины l заряженной линии.

8. Напряженность поля, создаваемого бесконечно прямой равномерно заряженной линией или бесконечно длинным цилиндром,

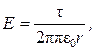
где r - расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

.

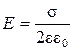9. Электрическое смещение (электрическая индукция)

.

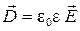Теорема Гаусса:

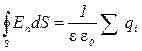или .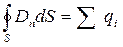

10. Связь потенциала с напряженностью:

а) 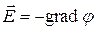или 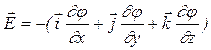в общем случае, где 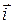, , 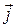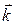- единичные векторы вдоль осей координат (орты);

б) 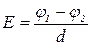в случае однородного поля;

в) 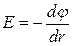в случае поля, обладающего центральной или осевой симметрией.

11. Электрический момент диполя

,

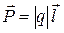где q – заряд; l - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

12. Работа сил поля по перемещению заряда q из точки поля с потенциалом j₁, в точку с потенциалом j₂

.

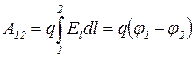13. Электроемкость уединенного тела и конденсатора

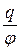С = , С = ,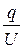

где j - потенциал проводника; U - разность потенциалов пластин конденсатора.

Следует помнить, что при изменении электрической емкости конденсатора, подключенного к источнику напряжения, меняется величина заряда на его пластинах, а разность потенциалов остается постоянной и равной э.д.с. источника тока. При изменении емкости конденсатора, отключенного от источника напряжения, меняется разность потенциалов на его пластинах, а величина заряда остается при этом неизменной.

Электроемкость плоского конденсатора

C = ,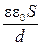

где S - площадь одной пластины конденсатора; d - расстояние между пластинами.

Электроемкость батареи конденсаторов:

а) 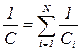при последовательном соединении;

б) 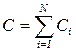при параллельном соединении,

где N - число конденсаторов в батарее.

Энергия заряженного конденсатора:

W = qU/2 =CU²/2 = q²/(2C),

,

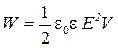где V – объем конденсатора.

Объемная плотность энергии электрического поля:

.

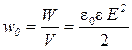14. Сила тока

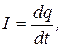
где q - заряд, прошедший через поперечное сечение проводника за время t.

Плотность тока

j = I / S,

где S - площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью 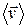упорядоченного движения заряженных частиц

,

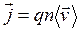где q - заряд частиц; n – их концентрация.

15. Закон Ома:

a) 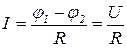для участка цепи, не содержащего э.д.с. (для однородного участка цепи), где j ₁ - j ₂ = U - разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;

б) 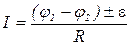для участка цепи, содержащего э.д.с. (для неоднородного участка цепи), где e - э.д.с. источника тока; R - полное сопротивление участка (сумма внешних и внутренних сопротивлений). Знаки «+» или «–» выбираются в зависимости от полярности включения источника.

в) 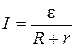для замкнутой (полной) цепи, где R - сопротивление внешней цепи, r - сопротивление внутреннее (сопротивление источника тока).

16. Правила Кирхгофа:

а) 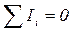- первое правило;

б) 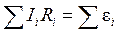- второе правило,

где 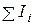- алгебраическая сумма сил токов, сходящихся в узле; 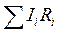- алгебраическая сумма произведений сил токов на сопротивления участков замкнутого контура; 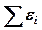- алгебраическая сумма э.д.с. в замкнутом контуре.

17. Сопротивление R и проводимость G однородного проводника

R = 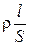, G = ,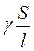

где r - удельное сопротивление; g - удельная проводимость; l - длина проводника; S - площадь поперечного сечения.

Зависимость удельного сопротивления от температуры

,

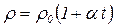где α – температурный коэффициент сопротивления, t – температура по шкале Цельсия.

Сопротивление системы проводников;

а) 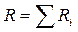- при последовательном соединении;

б) 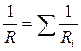- при параллельном соединении,

где R_i - сопротивление i - го проводника.

18. Работа тока:

.

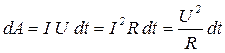Закон Джоуля-Ленца (тепловое действие тока):

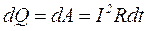
где dQ – количество теплоты, выделяющейся в проводнике, dt – промежуток времени, в течение которого выделялось тепло.

Мощность тока полной цепи:

P = I ε.

Мощность тока на внешнем участке цепи:

P = IU = I²R = U²/R.

Закон Ома в дифференциальной форме

.

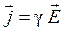Закон Джоуля-Ленца в дифференциальной форме

w = γ E²,

где w - объемная плотность тепловой мощности (количество тепла, выделяющегося в единице объема за единицу времени).

3.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

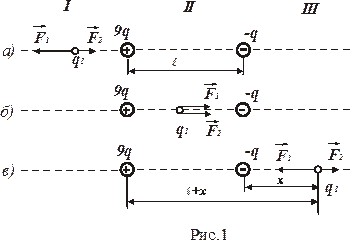№ 1. Два точечных заряда 9 q и - q закреплены на расстоянии l = 50 см друг от друга. Третий заряд q ₁ может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда q ₁, при котором он будет находиться в равновесии. При каком знаке заряда q ₁ равновесие будет устойчи­вым?

Р е ш е н и е.

Заряд q ₁ будет нахо­диться в равновесии в том случае, если геометрическая сумма сил, действующих на него, будет равна нулю. Это означает, что на заряд q ₁ должны действовать две силы, равные по величине и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (рис. 1) может быть выполнено это условие. Для определенности будем считать, что заряд q ₁ - положительный.

На участке I (рис. 1,а) на заряд q ₁ будут действовать две противоположно направленные силы F ₁ и F ₂. Сила F ₁, действующая со стороны заряда 9 q, в любой точке этого участка будет больше, чем сила F ₂, действующая со стороны заряда -q, так как больший (по абсолютной величине) заряд 9 q будет находиться всегда ближе к заряду q ₁, чем меньший заряд -q. Поэтому равновесие на этом участке невозможно.

На участке II (рис. 1,б) обе силы F ₁ и F ₂ направлены в одну сторону - к заряду -q. Следовательно, и на втором участке равновесие невозможно.

На участке III (рис. 1,в) силы F ₁ и F ₂ направлены в противоположные стороны, также как и на участке I, но в отличие от него меньший (по абсолютной величине) заряд (-q) всегда находится ближе к заряду q ₁, чем больший заряд 9 q. Это значит, что можно найти такую точку на прямой, где силы F ₁ и F ₂ будут одинаковы по абсолютной величине, т.е.

F₁ = F₂. (1)

Пусть расстояние от меньшего заряда до заряда q ₁ будет х, тогда расстояние от большегоl + х. Заменяя в равенстве (1) F ₁ и F ₂ в соответствии с законом Кулона, получим для абсолютной величины этих сил:

.

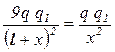Сокращая на qq ₁ и извлекая из обеих частей равенства корень квадратный, найдем

l + х = Зх,

откуда

х = + 1/2.

Определим знак заряда q ₁, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда q ₁ в двух случаях: когда заряд положителен и когда заряд отрицателен.

Если заряд q ₁ положителен, то при смещении его влево обе силы F ₁ и F ₂ возрастают. Но F ₂ (по абсолютному значению) больше, чем F ₁, и на заряд q ₁ будет действовать результирующая сила, направленная также влево. Под действием этой силы заряд q ₁ удаляется от положения равновесия. То же происходит и при смещении заряда q ₁ вправо. Сила F ₂ будет убывать быстрее, чем F ₁. Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т.е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.

Если заряд q ₁ отрицателен, то его смещение влево вызовет увеличение сил F ₁ и F ₂, но сила F₁ возрастает медленнее, чем F ₂, т.е. |F₂| > | F ₁|. Результирующая сила будет направлена вправо. Под действием этой силы заряд q ₁ возвращается к положению равновесия. При смещении q ₁ вправо сила F ₂ убывает быстрее, чем F ₁, т.е. | F ₁| > | F ₂|, результирующая сила направлена влево и заряд q ₁ опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда q ₁ несущественна.

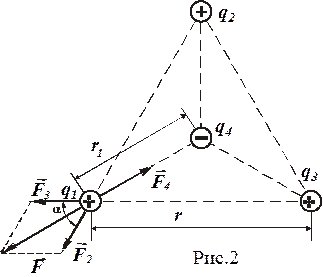
№ 2. Три точечных заряда q₁ = q₂ = q₃ = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд q ₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Р е ш е н и е.

Все три заряда, распо­ло­жен­ные по вершинам треу­голь­ника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треу­голь­ника, чтобы какой-нибудь один из трех зарядов, например q ₁, находился в равновесии. Заряд q ₁ будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис 2):

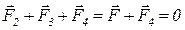, (1)

где 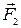, , 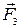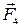- силы, с которыми соответственно действуют на заряд q ₁ заряды q ₂, q ₃, q ₄; 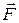- равнодействующая сил 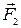и .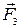

Так как силы 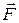и 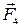направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным равенством F – F₄ = 0, откуда

F₄ = F.

Выразив в последнем равенстве F через F ₂ и F ₃ и учитывая, что F₃ = F ₂, получим .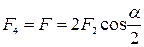

Применяя закон Кулона, и имея в виду, что q₂ = q₃ = q₁, найдем

,

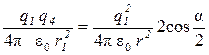откуда

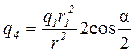. (2)

Из геометрических построений в равностороннем треугольнике (α =60°) следует, что

.

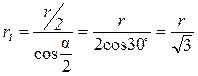С учетом этого формула (2) примет вид

.

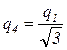Подставив числовое значение q ₁ = 1 нКл = 10^-9Кл, получим

.

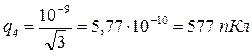Следует отметить, что равновесие системы зарядов будет неустойчивым.

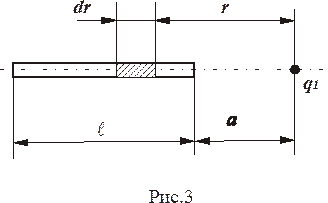№ 3. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд q₁ = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плот­ность τ заряда на стержне.

Р е ш е н и е.

При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. Выделим на стержне (рис. 3) малый участок dr с зарядом dq = τdr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,

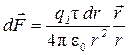, (1)

где 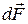- сила взаимодействия заряда q ₁ и заряда, участка dr. Так как все 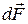сонаправлены, можно воспользоваться скалярным выражением для :

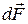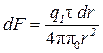(2)

Интегрируя это выражение в пределах от а до а+ l, получим

,

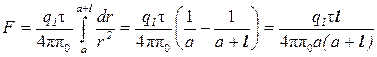откуда интересующая нас линейная плотность заряда равна

.

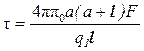Выразим все величины в единицах СИ: q ₁ = 40 нКл = 4·10^-8Kл, F = 6 мкН = 6·10^-6 Н, l = 0,2м, а = 0,1м, 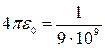Ф/м., ε ₀ = 8,85·10^-12 Ф/м.

Подставим числовые значения величин в полученную формулу и произведем вычисления:

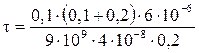Кл/м = 2,5·10^-9 Кл/м = 2,5 нКл/м.

№ 4. Два точечных электрических заряда q ₁ = 1 нКл и q ₂ = -2 нКл находятся в воздухе на расстоянии d = 10см друг от друга. Определить напряженность 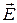и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда q ₁, на расстояние r ₁ = 9 см и от заряда q ₂ на r ₁ = 7 см.

Р е ш е н и е.

Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность 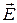электрического поля в искомой точке может быть найдена как геометрическая сумма напряженносте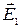й и 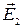полей, создаваемых каждым зарядом в отдельности: 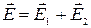. Напряженность электрического поля, создаваемого в воздухе (ε = 1) зарядом q ₁, равна

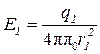, (1)

зарядом q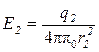₂ -

. (2)

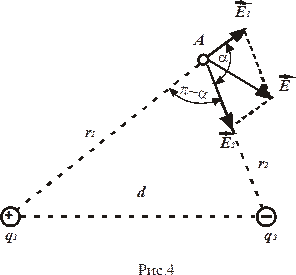
Вектор 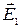(рис. 4) направлен по силовой линии от заряда q ₁, так как заряд q ₁ положителен; вектор 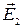направлен также по силовой линии, но к заряду q₂, так как заряд q ₂ отрицателен.

Абсолютное значение вектора Е найдем как следствие из теоремы косинусов:

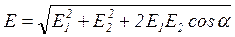, (3)

где α – угол между векторам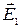и и 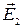, который может быть найден из треугольника со сторонами r ₁, r ₂ и d по теореме косинусов:

,

.

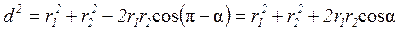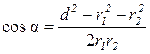В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:

.

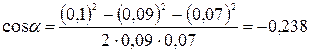Подставляя выражение Е₁, из формулы (1) и E₂ из формулы (2) в равенство (3) и вынося общий множитель 1/(4πε₀ ) за знак корня, получим

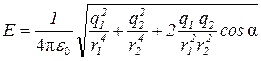. (4)

Подставим числовые значения величин в формулу (4) и произведем вычисления:

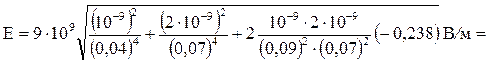3,58 кВ/м.

При вычислении Е знак заряда q ₂ опущен, так как знак заряда определяет направление вектора напряженности, а направление 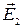было учтено при его графическом изображении (рис. 4).

В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами q ₁ и q ₂, равен алгебраической сумме потенциалов, т. е.

φ = φ₁ + φ₂. (5)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом q на расстоянии г от него, выражается формулой

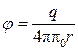. (6)

В нашем случае согласно формулам (5) и (6) получим

,

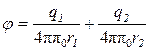или

.

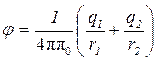Подставляя в это выражение числовые значения физических величин, получим

.

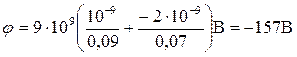№ 5. Точечный заряд q = 25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R = 1 см, равномерно заряженным с поверхностной плотностью σ = 0,2 нКл/см², Определить силу F, действующую на заряд, если его расстояние от оси цилиндра r = 10 см.

Р е ш е н и е.

Численное значение силы F, действующей на точечный заряд q, находящийся в поле, определяется по формуле

F = qE, (1)

где Е - напряженность поля, создаваемого заряженным цилиндром.

Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра

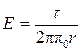, (2)

где τ - линейная плотность заряда.

Выразим линейную плотность τ через поверхностную плотность σ. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд q двумя способами:

q = σS = σ · 2·π ·Rl; q = τ L.

Приравняв правые части этих равенств, и сократив на l, получим

τ = 2π ·R σ.

С учетом этого формула (2) примет вид

.

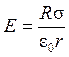Подставив это выражение в (1), получим искомую силу F:

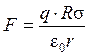. (3)

Выпишем в единицах СИ числовые значения величин: q = 25 нКл = 2,5·10^-8 Кл, σ =0,2 нКл/см² = 2·10^-6 Кл/м², ε ₀ = 8,85·10^-12 Ф/м. Так как R и r входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах. Подставим в (3) числовые значения величин:

.

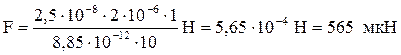Направление силы 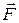совпадает с направлением напряженности 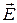, а последняя направлена перпендикулярно поверхности цилиндра.

№ 6. Две концентрические проводящие сферы радиусами R₁ = 6 см и R ₂ = 10 см несут соответственно заряды q ₁ = 1 нКл и q ₂ = -0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r ₁ = 5 см, r ₂ = 9 см, r ₃ = 15 см.

Р е ш е н и е.

Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (см. рис. 5): области I (r ₁ < R ₁), области II (R ₁ < r ₂ < R ₂), области III (r ₃ > R ₂).

1. Для определения напряженности Е ₁ в области I проведем замкнутую сферическую поверхность S ₁ радиусом r ₁ и воспользуемся теоремой Гаусса:

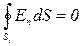
(так как суммарный заряд, находящийся внутри данной замкнутой поверхности, равен нулю). Следовательно, Е ₁ (напряженность поля в области I) во всех точках, удовлетворяющих условию r₁ < R ₁, будет равна нулю.

2. В области II замкнутую поверхность проведем радиусом r ₂. В этом случае

,

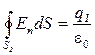(так как внутри этой замкнутой поверхности находится только заряд q ₁).

Так как Е_n = Е = const, то Е можно вынести за знак интеграла:

,

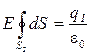или

.

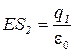Обозначив напряженность Е для области II через Е₂, получим

,

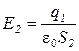где S₂ = 4π·r ₂² – площадь замкнутой сферической поверхности. Тогда

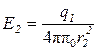. (1)

3. В области III сферическая поверхность проводится радиусом r ₃. Обозначим напряженность Е области III через Е ₃ и учтем, что в этом случае замкнутая поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен q₁ + q₂. Тогда

.

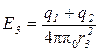Выразим все величины в единицах Си (q ₁ = 10^-9 Кл, q ₂ = -0,5·10^-9Кл, r₁ = 0,05 м, r ₂ = 0,09 м, r ₃ = 0,15 м, 1/(4πε₀) = 9·10⁹ м/Ф) и произведем вычисления

;

.

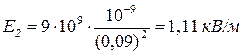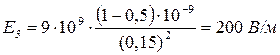№ 7. По тонкой нити, изогнутой по дуге окружности равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Определить напряженность Е и потенциал φ электрического поля, создава­емого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина l нити составляет одну треть длины окружности и равна 16 см.

Р е ш е н и е.

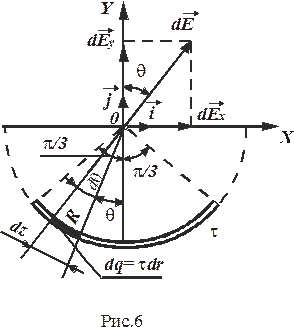
Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена отно­си­тельно концов дуги (рис. 6).

На нити выделим элемент длины dl. Заряд dq = τdl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке 0. Для этого найдем сначала напряженность 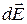поля, создаваемого зарядом dq:

,

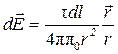где r - радиус-вектор, направленный от элемента dl к точке, напряженность в которой вычисляется.

Выразим вектор 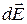через проекции dE_х и dE_у на оси координат:

,

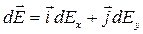где 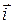и 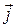- единичные векторы направлений (орты).

Напряженность 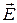найдем интегрированием:

.

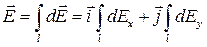Интегрирование ведется вдоль дуги длины l. В силу симметрии интеграл 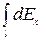равен нулю. Тогда

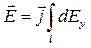, (1)

где .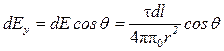

Так как r = R = const, dl = Rdθ, то .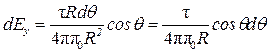

Подставим найденное значение dE_у в выражение (1)и, приняв во внимание симметричное расположение дуги относительно оси Y, пределы интегрирования возьмем от 0 до π/З, а результат удвоим:

.

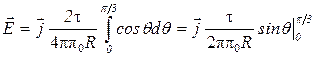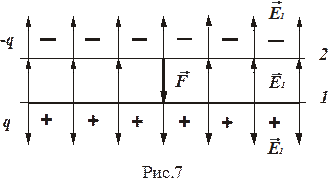Подставив указанные пределы и выразив R через длину дуги (3·l = 2πR), получим

.

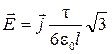Из этой формулы видно, что вектор 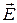совпадает с положительным направлением оси Y.

Подставим значения τ и l в полученную формулу и произведем вычисления:

.

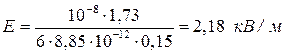Найдем потенциал электрического поля в точке 0. Сначала найдем потенциал dφ, создаваемый точечным зарядом dq в точке 0:

.

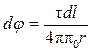Заменим r на R и произведем интегрирование:

.

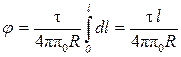Так как l = 2πR/З, то φ = τ /6 ε₀. Произведем вычисления:

.

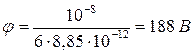№ 8. На пластинах плоского конденсатора находится заряд q = 10 нКл. Площадь S каждой пластины конденсатора равна 100 см², диэлектрик - воздух. Опреде­лить силу F, с которой притягиваются пластины.

Р е ш е н и е.

Заряд q второй пластины находится в поле напряженностью Е ₁, созданном зарядом первой пластины конденсатора. Следовательно, на заряд q действует сила (рис. 7)

F = qE₁. (1)

Так как

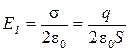, (2)

где σ - поверхностная плотность заряда пластины, то формула (1) с учетом выражения (2) примет вид

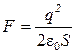. (3)

Подставив числовые значения величин в формулу (3), подучим

.

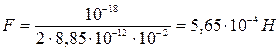№ 9. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии а ₁ = 0,5 см и а ₂ = 2 см от поверхности цилиндра в средней его части.

Р е ш е н и е.

Для определения разности потенциалов воспользуемся соотно­шением между напряженностью поля и изменением потенциала:

.

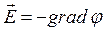Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

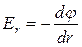, или dφ = - E_r dr.

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r ₁ и r ₂ от оси цилиндра:

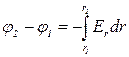. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для напряженности можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:

.

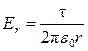Подставив выражение Е в (1), подучим

,

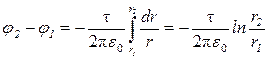или

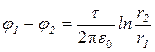. (2)

Выразим τ и 1/2πε₀ в единицах СИ: τ = 20 нКл/м = 2·10^-8 Кл/м, ε ₀ = 8,85·10^-12 Ф/м.

Так как величины r ₁ и r ₂ входят в формулу (2) в виде отношения, их можно выразить в любых, но только одинаковых единицах: r₁ = R + а₁ = 1,5 см; r₂= R + а₂ = 3 см. Подставим числовые значения в (2) и вычислим:

.

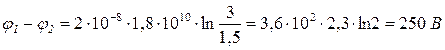№ 10. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью v₁ = 10⁶ м/с, чтобы скорость его возросла в n = 2 раза.

Р е ш е н и е.

Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением заряда электрона е на разность потенциалов U:

А = eU (1)

Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:

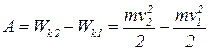, (2)

где W_К1 и W_К2 - кинетические энергии электрона до и после прохождения ускоряющего поля; m - масса электрона; v ₁ и v ₂ - начальная и конечная скорости его.