При анализе многих экономических показателей приходится сравнивать две генеральные совокупности. Например, можно сравнивать уровни жизни в двух странах по размеру дохода на душу населения; можно сравнивать два варианта инвестирования по размерам средних дивидендов; качество знаний студентов двух университетов – по среднему баллу на комплексном тестовом экзамене. В этих случаях логично провести сравнение по схеме анализа равенства математических ожиданий двух генеральных совокупностей X и Y.
Рассмотрим две случайные величины X ~ N (a 1,s1) и Y~ N (a 2,s2), каждая из которых подчиняется нормальному закону распределения. Пусть имеются две независимые выборки с объемами n 1 и n 2 из генеральных совокупностей X и Y. Необходимо проверить нулевую гипотезу H 0: M[ X ]=M[ Y ]. Нулевая гипотеза в приведенной формулировке является сложной, поскольку она справедлива при любых a =M[ X ]=M[ Y ], однако она может быть сведена к простой, если рассматривать разность средних, т.е. H 0: M[ X ]–M[ Y ]=0.
Относительно параметров 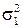 и
и 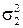 можно выделить четыре варианта предположений:
можно выделить четыре варианта предположений:
a) обе дисперсии известны и равны между собой;
b) обе дисперсии известны, но неравны между собой;
c) обе дисперсии неизвестны, но предполагается, что они равны между собой;
d) обе дисперсии неизвестны и их равенство не предполагается.
Критерии проверки гипотез о числовых значениях параметров нормального распределения приведены в таблице 3.8. Отметим, что в таблице 3.8 вариант a) рассматривается как частный случай варианта b). В случае неизвестных дисперсий, равенство которых не предполагается, используется аналог статистики варианта b) с заменой неизвестных дисперсий их оценками
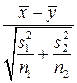 . (3.29)
. (3.29)
В этой ситуации указать точное распределение введенной статистики затруднительно. Известно, однако, что это распределение близко к распределению Стьюдента с числом степеней свободы, равным
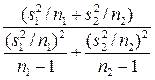 . (3.30)
. (3.30)
Критерий проверки устроен так же, как и для варианта c).
Таким образом, для выбора подходящей проверочной статистики в случае, когда генеральные дисперсии неизвестны, необходимо знать, какое предположение принимается. Прежде всего нужно решить, можно ли считать неизвестные генеральные дисперсии равными или нет. Для принятия решения используют F -критерий Фишера (см. далее).
Таблица 3.9
| H 0 | Предположения | Статистика критерия | H 1 | Область принятия решения |
| a 1= a 2 | 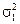 , , 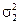 известны известны | 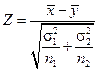 | a 1¹ a 2 | 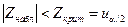 |
| a 1> a 2 | 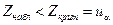 | |||
| a 1< a 2 | 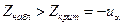 | |||
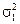 , , 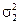 неизвестны, но равны неизвестны, но равны | 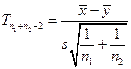 , где , где 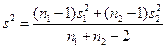 | a 1¹ a 2 | 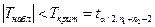 | |
| a 1> a 2 | 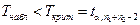 | |||
| a 1< a 2 | 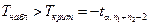 |
Зачастую при сравнении двух экономических показателей на первый план выходит анализ разброса значений рассматриваемых случайных величин. Например, при решении вопроса об инвестировании в одну из двух отраслей остро стоит проблема риска вложений. При сравнении уровней жизни в двух странах среднедушевые доходы могут оказаться приблизительно равными. Сопоставив разброс в доходах, мы получаем более точное представление о них. Анализ, аналогичный описанному выше, целесообразно проводить путем сравнения дисперсий исследуемых случайных величин.
Пусть X ~ N (a 1,s1) и Y~ N (a 2,s2), причем их средне квадратичные отклонения s1 и s2 неизвестны. Выдвигается гипотеза о равенстве дисперсий 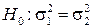 . Однако это гипотеза в приведенной формулировке является сложной, поэтому вместо этой гипотезы рассматривается другая, простая гипотеза об отношении дисперсий, т.е.
. Однако это гипотеза в приведенной формулировке является сложной, поэтому вместо этой гипотезы рассматривается другая, простая гипотеза об отношении дисперсий, т.е. 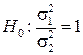 .
.
В качестве критерия проверки гипотезы H 0 принимают случайную величину
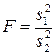 , (3.31)
, (3.31)
определяемую отношение большей исправленной выборочной дисперсии к меньшей (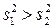 ). Если нулевая гипотеза H 0 верна, то данная статистика имеет F -распределение Фишера с n1= n 1–1 и n2= n 2–1 степенями свободы. Различные случаи использования этого критерия Фишера приведены в таблице 3.8.
). Если нулевая гипотеза H 0 верна, то данная статистика имеет F -распределение Фишера с n1= n 1–1 и n2= n 2–1 степенями свободы. Различные случаи использования этого критерия Фишера приведены в таблице 3.8.
Таблица 3.8
| H 0 | Предположения | Статистика критерия | H 1 | Область принятия решения |
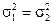 | a 1, a 2 неизвестны | 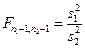 , ( , (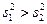 ) ) | 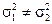 | 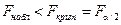 |
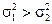 | 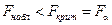 |
Пример 3.14. Компания по производству сахарного песка имеет производственные линии для наполнения мешочков сахарным песком по 1 кг. Используя данные, собранные в течение долгого периода времени, управляющий оценивает генеральное стандартное отклонение массы мешочков, поставляемых с линии А в 0,02 кг (s1) и с линии B в 0,04 кг (s2). Из линии A была взята случайная выборка объемом n 1=10 мешочков и найдена средняя масса содержимого в мешочках 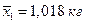 . Подобная выборка объемом n 2=12 мешочков была взята из линии B и найдена средняя масса
. Подобная выборка объемом n 2=12 мешочков была взята из линии B и найдена средняя масса 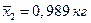 . Имеется ли какое-нибудь основание предполагать, что две производственные линии развешивают сахарный песок по мешочкам, средняя масса которых отличается?
. Имеется ли какое-нибудь основание предполагать, что две производственные линии развешивают сахарный песок по мешочкам, средняя масса которых отличается?
Решение. Сформулируем основную и альтернативную гипотезы, соответствующие условию задачи:
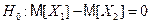 ,
, 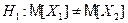 .
.
Поскольку генеральные дисперсии (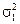 и
и 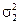 ) известны, проверим существенность разности между выборочными средними, используя нормальное распределение на уровне значимости a=0,01. Вычисляем наблюдаемое значение критерия
) известны, проверим существенность разности между выборочными средними, используя нормальное распределение на уровне значимости a=0,01. Вычисляем наблюдаемое значение критерия
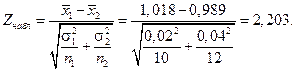
Поскольку критическая область имеет двухсторонний вид, то критическое значение критерия будет определяется из условия
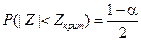 ,
,
или
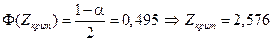 .
.
В результате получаем, что | Zнабл| <Z крит, т.е. нет оснований отклонять нулевую гипотезу. Следовательно, можно полагать, что мешочки, наполненные сахаром на двух производственных линиях, имеют одинаковую среднюю массу. â
Пример 3.15. Для исследования качества масла были сделаны выборки по 10 единиц из каждой последовательной серии (n 1 и n 2) и определена доля воды в процентах x в каждой выборке. В первой серии средний процент составил 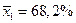 с исправленным средним квадратичным отклонением
с исправленным средним квадратичным отклонением 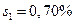 . Для второй серии средний процент воды составил
. Для второй серии средний процент воды составил 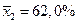 со средним квадратичным отклонением
со средним квадратичным отклонением 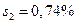 . Имеются ли основания предполагать на 5%-ом уровне значимости, что две серии масла имеют различную массовую долю воды?
. Имеются ли основания предполагать на 5%-ом уровне значимости, что две серии масла имеют различную массовую долю воды?
Решение. Сформулируем основную и альтернативную гипотезы, соответствующие условию задачи:
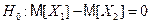 ,
, 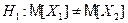 .
.
Поскольку генеральные дисперсии (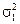 и
и 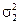 ) неизвестны, то следует предварительно проверить о равенстве генеральных дисперсий, т.е. проверяем нулевую гипотезу с соответствующей альтернативной гипотезой:
) неизвестны, то следует предварительно проверить о равенстве генеральных дисперсий, т.е. проверяем нулевую гипотезу с соответствующей альтернативной гипотезой:
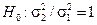 ,
, 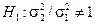 .
.
наблюдаемое значение критерия Фишера:
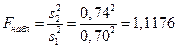 .
.
Здесь учено, что 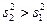 . Поскольку, в соответствии с выбранной альтернативной гипотезой, критическая область будет двухсторонней, то определяет критической значение критерия Фишера:
. Поскольку, в соответствии с выбранной альтернативной гипотезой, критическая область будет двухсторонней, то определяет критической значение критерия Фишера:
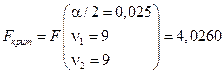
В результате получаем, что Fнабл <F крит, т.е. нет оснований отклонять нулевую гипотезу. Следовательно, можно полагать, что две генеральные дисперсии раны друг другу.
Продолжим теперь испытание гипотез о равенстве двух генеральных средних. Для этого вычислим наблюдаемое значение соответствующего критерия Стьюдента:
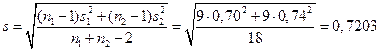 ,
,
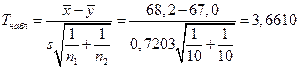 .
.
Поскольку критическая область также будет двухсторонней, то соответствующая критическое значение критерия Стьюдента будет равно:
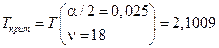 .
.
В результате получаем, что Tнабл > Tкрит, т.е. нулевая гипотеза отклоняется. Следовательно, можно полагать, что две серии проб имеют разное содержание воды (по массе).
 2015-10-13
2015-10-13 1997
1997
