Прокомментируем теперь более подробно основные этапы всей процедуры проверки на примере задачи сравнения с эталоном при заданном  .
.
1. Постановка задачи. Формулируем основную гипотезу:  :
: 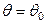
(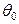 - эталон. В дальнейшем нас будет интересовать проверка гипотез, связанных с тремя основными характеристиками: математическим ожиданием, дисперсией (или среднеквадратичным отклонением) и вероятностью какого либо интересующего нас события:
- эталон. В дальнейшем нас будет интересовать проверка гипотез, связанных с тремя основными характеристиками: математическим ожиданием, дисперсией (или среднеквадратичным отклонением) и вероятностью какого либо интересующего нас события: 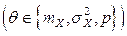 ).
).
Конкретизируем одну из трех возможных альтернатив:
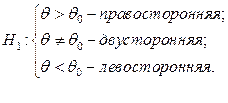
2) Выбор критической области.
Прежде всего отметим, что в результате применения указанного выше решающего правила ни в коем случае нельзя установить истинность гипотезы  . Может найтись другая гипотеза, так же хорошо согласующаяся с опытными данными, как и первая. С другой стороны, каждая конкретная процедура проверки статистической гипотезы может привести к ошибочному решению. Действительно, может оказаться, что выборочное значение статистики попало в критическую область, и мы отклонили гипотезу
. Может найтись другая гипотеза, так же хорошо согласующаяся с опытными данными, как и первая. С другой стороны, каждая конкретная процедура проверки статистической гипотезы может привести к ошибочному решению. Действительно, может оказаться, что выборочное значение статистики попало в критическую область, и мы отклонили гипотезу  , в то время как на самом деле она верна. Тем самым мы совершили так называемую ошибку первого рода: «отвергнуть правильную гипотезу». Вероятность совершить такую ошибку, как следует из формулы (5.1.1) равна уровню значимости
, в то время как на самом деле она верна. Тем самым мы совершили так называемую ошибку первого рода: «отвергнуть правильную гипотезу». Вероятность совершить такую ошибку, как следует из формулы (5.1.1) равна уровню значимости  .
.
Наряду с этим может быть совершена так называемая ошибка второго рода: «принять ложную гипотезу». Это произойдет в том случае, когда 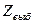 попадет в допустимую область
попадет в допустимую область 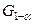 и будет принято решение в пользу
и будет принято решение в пользу  , в то время как на самом деле верна гипотеза
, в то время как на самом деле верна гипотеза 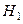 . Вероятность ошибки второго рода определяется уравнением:
. Вероятность ошибки второго рода определяется уравнением:
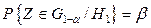 (5.1.2)
(5.1.2)
Вероятность противоположного события:
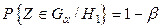
называют мощностью правила выбора решения. Она определяет вероятность «отвергнуть ложную гипотезу».
Ошибки при принятии решения принципиально неустранимы, что определяется случайной природой статистики 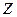 , и далеко не равнозначны, так как могут приводить к различным последствиям. Чтобы проиллюстрировать сказанное, рассмотрим два примера с различными постановками задачи проверки гипотез.
, и далеко не равнозначны, так как могут приводить к различным последствиям. Чтобы проиллюстрировать сказанное, рассмотрим два примера с различными постановками задачи проверки гипотез.
Пример 5.1.1. В задаче радиолокационного обнаружения цели проверяется основная гипотеза  , утверждающая, что цель своя. Альтернативой служит гипотеза
, утверждающая, что цель своя. Альтернативой служит гипотеза 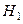 , утверждающая, что цель чужая. Выяснить логику ошибок первого и второго рода.
, утверждающая, что цель чужая. Выяснить логику ошибок первого и второго рода.
◄ Ошибка первого рода, имеющая смысл «отвергнуть правильную гипотезу», в данном случае означает, что своя цель будет принята за чужую, и трактуется как «ложная тревога». Ошибка второго рода, имеющая смысл «принять ложную гипотезу», в данном случае означает, что чужая цель будет принята за свою. Предоставляем читателю самостоятельно поразмышлять о сравнительных последствиях этих двух ошибок.►
Пример 5.1.2. Цех выпустил партию деталей (например, интегральных схем) с неизвестным процентом брака. Поставщик утверждает, что этот процент находится в пределах норматива, оговоренного в договоре с заказчиком (равен эталонному значению). Заказчик, напротив, утверждает, что по некоторым его наблюдениям этот процент значительно превышен. Возникает конфликт, для разрешения которого решено провести эксперимент: наудачу отобрать определенное количество деталей и вычислить процент бракованных. Договорившись об уровне значимости  , конфликтующие стороны решили проверить основную гипотезу
, конфликтующие стороны решили проверить основную гипотезу  против правосторонней альтернативы
против правосторонней альтернативы 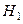 и тем самым разрешить свой спор на высоком научно-методическом уровне. Ответить на следующие вопросы:
и тем самым разрешить свой спор на высоком научно-методическом уровне. Ответить на следующие вопросы:
1) Каков смысл ошибок первого и второго рода?
2) Каковы возможные последствия для производства от этих ошибок?
◄ 1) Ошибка первого рода: забракована хорошая партия (интерпретируется как «ложная тревога»),- страдает поставщик. Ошибка второго рода: принята плохая партия (интерпретируется как «пропуск цели»),- в результате этой ошибки страдает заказчик.
2) В действительности, если глубже взглянуть на всю проблему производства и сбыта в целом, получится, что ущерб наносится производству. Если, например, будет забракована хорошая партия (совершена ошибка первого рода), то поставщик не выполнит план поставок, что может привести к задержке или срыву плана производства. Если же будет принята плохая партия (совершена ошибка второго рода), то это может повредить не только репутации заказчика, но и той продукции, для которой предназначались закупленные плохие интегральные схемы.►
Вернемся снова к задаче выбора критической области. Еще раз отметим, что согласно уравнению (5.1.1) критическая область напрямую зависит от уровня значимости  . Однако выбор самого
. Однако выбор самого  не является задачей математической статистики. Напротив, метод проверки статистической гипотезы начинает работать с момента, когда
не является задачей математической статистики. Напротив, метод проверки статистической гипотезы начинает работать с момента, когда  уже определено. При выборе
уже определено. При выборе  в конкретной физической ситуации обычно руководствуются тем, какие последствия могут повлечь за собой неправильно принятые решения в пользу конкурирующей гипотезы. В одних случаях, например, достаточно пренебречь событиями, имеющими вероятность меньшую, чем 0,05, в других, если речь идет о гибели пассажирского самолета или разрушении железнодорожного моста, нельзя пренебречь и событием, имеющим вероятность 0,001.
в конкретной физической ситуации обычно руководствуются тем, какие последствия могут повлечь за собой неправильно принятые решения в пользу конкурирующей гипотезы. В одних случаях, например, достаточно пренебречь событиями, имеющими вероятность меньшую, чем 0,05, в других, если речь идет о гибели пассажирского самолета или разрушении железнодорожного моста, нельзя пренебречь и событием, имеющим вероятность 0,001.
Идеальным было бы такое решение, когда можно одновременно уменьшить обе ошибки первого и второго рода до нужного уровня. К сожалению, такое решение неосуществимо, так как попытка уменьшить  за счет уменьшения критической области
за счет уменьшения критической области 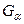 немедленно приведет к увеличению ошибки второго рода
немедленно приведет к увеличению ошибки второго рода 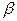 , поскольку автоматически увеличится допустимая область
, поскольку автоматически увеличится допустимая область 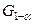 . Однако можно, не изменяя размеров критической области, менять ее расположение в
. Однако можно, не изменяя размеров критической области, менять ее расположение в 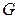 и тем самым попытаться уменьшить
и тем самым попытаться уменьшить 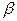 . Такой подход оправдан в ситуациях, когда ошибка второго рода не приводит к катастрофическим последствиям.
. Такой подход оправдан в ситуациях, когда ошибка второго рода не приводит к катастрофическим последствиям.
Поэтому задача выбора критической области ставится как следующая задача оптимизации:
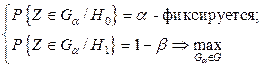 (5.1.3)
(5.1.3)
Таким образом, оптимизационная задача состоит в таком выборе критической области 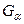 , чтобы при фиксированном
, чтобы при фиксированном  максимизировать мощность критерия (минимизировать ошибку II рода). Заметим, что решение задачи (5.1.3) существенно зависит от двух обстоятельств: от формулировки альтернативы и характера распределения статистики Z. Приведем соответствующие результаты для важнейших видов распределений, имея в виду задачу сравнения с эталоном.
максимизировать мощность критерия (минимизировать ошибку II рода). Заметим, что решение задачи (5.1.3) существенно зависит от двух обстоятельств: от формулировки альтернативы и характера распределения статистики Z. Приведем соответствующие результаты для важнейших видов распределений, имея в виду задачу сравнения с эталоном.
I вид распределения статистики: симметричный относительно начала координат (нормальный, Стьюдента и т.п.) –.
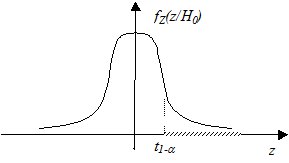 | 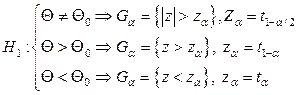 |
На рисунке заштрихована правосторонняя критическая область, соответствующая альтернативе: 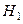 :
: 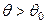 .
.
II вид распределения статистики: несимметричный (распределения 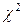 , Фишера).
, Фишера).
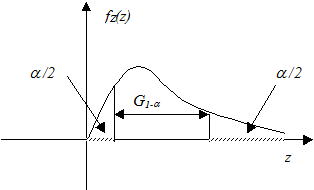 | 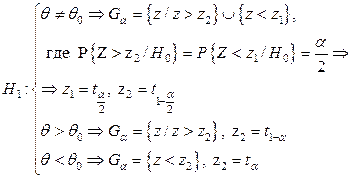 |
На рисунке заштрихована двусторонняя критическая область, соответствующая альтернатива: 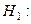
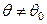 .
.
3) Выбор подходящей статистики.
Для проверки статистических гипотез о сравнении с эталоном по существу используются те же статистики, которые использовались для построения доверительного интервала. Эти статистики подробно изучались в гл.4 и приводятся в сводной таблице (4.5.1).
Напомним вид тех статистик, которые используются для проверки гипотезы о сравнении с эталоном для трех основных параметров.
Пусть генеральная случайная величина 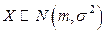 . Проверяется основная гипотеза
. Проверяется основная гипотеза  : mX=m0 против одной из альтернатив. Рассмотрим два случая:
: mX=m0 против одной из альтернатив. Рассмотрим два случая:
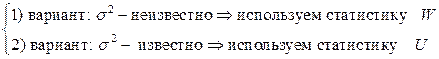
где обозначено 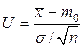 ~N(0,1), (см. формулу (4.5.4), в которой
~N(0,1), (см. формулу (4.5.4), в которой 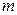 заменено на
заменено на 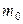 в силу утверждения гипотезы
в силу утверждения гипотезы  );
);
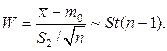 (см. упражнение (4.5.1)). Напомним, что
(см. упражнение (4.5.1)). Напомним, что 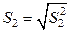 , где
, где 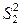 - так называемая исправленная выборочная дисперсия.
- так называемая исправленная выборочная дисперсия.
Для проверки основной гипотезы о дисперсии:  :
: 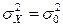 против одной из альтернатив
против одной из альтернатив 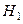 рассмотрим также два случая:
рассмотрим также два случая:
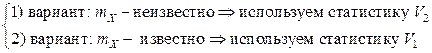
Здесь обозначено 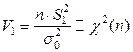 , где
, где 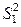 - несмещенная выборочная дисперсия при известном мат.ожидании;
- несмещенная выборочная дисперсия при известном мат.ожидании;
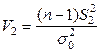
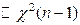 .
.
При аналогичной постановке задачи для параметра 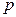 (
( :
: 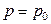 ) используем статистику:
) используем статистику:
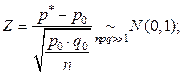
Здесь 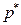 - относительная частота успехов в
- относительная частота успехов в 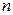 опытах по схеме Бернулли. Закон распределения указанной статистики
опытах по схеме Бернулли. Закон распределения указанной статистики 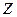 обосновывается в примере 4.6.5.
обосновывается в примере 4.6.5.
Рассмотрим несколько характерных примеров на сравнение с эталоном
Пример 5.1.3. Время реакции на световой сигнал среди водителей-профессионалов должно находиться на уровне»3сек. для безопасной езды в темное время суток (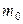 =3 сек.). Тестирования, проведенные среди 16 водителей дали следующие результаты:
=3 сек.). Тестирования, проведенные среди 16 водителей дали следующие результаты: 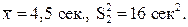
1) Следует ли из этих данных, что время реакции испытуемых значимо больше номинального на уровне значимости 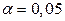 ?
?
2) Что изменится если выбрать 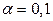 ?
?
3) Что изменится если известно, что 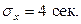 ?
?
4) Можно ли считать, что время реакции водителей значимо отличается от номинального?
 Формулируем задачу проверки следующим образом:
Формулируем задачу проверки следующим образом:
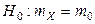 ;
;
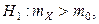 Þ подходящей статистикой является
Þ подходящей статистикой является 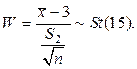
Как установлено в 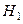 , критическая область – правосторонняя Þ по таблице квантилей распределения Стьюдента находим
, критическая область – правосторонняя Þ по таблице квантилей распределения Стьюдента находим
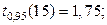
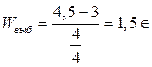
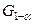
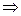
1)  принимается на данном уровне значимости
принимается на данном уровне значимости  . Другими словами, выборочные данные не подтверждают гипотезу
. Другими словами, выборочные данные не подтверждают гипотезу 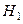 о том, что время реакции испытуемых значимо больше номинального.
о том, что время реакции испытуемых значимо больше номинального.
2) Ответ: если 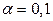 то
то  – отвергается.
– отвергается.
3) Изменяется статистика (можно использовать 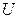 ) и квантиль Þ
) и квантиль Þ 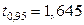 (из таблицы нормального распределения). Т.к.
(из таблицы нормального распределения). Т.к. 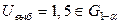 , то
, то  – принимается.
– принимается.
4) Постановка задачи в этом случае имеет вид:
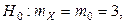
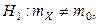
Þ подходящая статистика 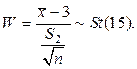
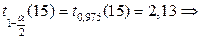
 подтверждается с большей степенью надежности.
подтверждается с большей степенью надежности. 
Пример 5.1.4. В результате длительного хронометража времени сборки узла различными сборщиками установлено, что дисперсия этого времени 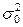 =2 мин2. Проведено двадцать наблюдений за работой новичка, давших следующие результаты:
=2 мин2. Проведено двадцать наблюдений за работой новичка, давших следующие результаты:
Время сборки узла 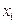 , мин , мин | |||||
Число случаев 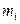 |
Можно ли на уровне значимости  =0,05 считать, что новичок работает ритмично (в том смысле, что дисперсия затрачиваемого им времени сборки значимо не отличается от дисперсии эталонного времени сборки остальных сборщиков)?
=0,05 считать, что новичок работает ритмично (в том смысле, что дисперсия затрачиваемого им времени сборки значимо не отличается от дисперсии эталонного времени сборки остальных сборщиков)?
◄ Пусть 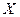 время сборки узла новичком. Считаем, что
время сборки узла новичком. Считаем, что 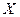 распределена нормально
распределена нормально 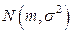 . Требуется проверить основную гипотезу
. Требуется проверить основную гипотезу 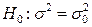 =2 против двусторонней альтернативы
=2 против двусторонней альтернативы 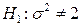 . Так как математическое ожидание неизвестно, то подходящей статистикой является
. Так как математическое ожидание неизвестно, то подходящей статистикой является
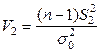 , распределенная по закону
, распределенная по закону 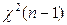 .
.
Вычисляем оценки 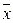 и
и 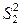 по формулам для частотной выборки объема
по формулам для частотной выборки объема 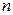 =20:
=20:
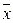 =
= 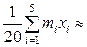 60;
60; 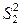 =
= 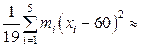 =4.
=4.
Отсюда получаем выборочное значение статистики 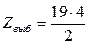 =38.
=38.
Учитывая, что альтернатива двусторонняя и используя таблицу квантилей распределения хи-квадрат, находим границы двусторонней критической области: левая граница: 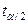 (19)=8,91; правая граница:
(19)=8,91; правая граница: 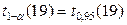 =30,1. Таким образом, критическая область имеет вид
=30,1. Таким образом, критическая область имеет вид 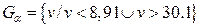 . Поскольку
. Поскольку 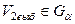 , то гипотезу
, то гипотезу  следует отвергнуть на данном уровне значимости как не соответствующую опытным данным. Следовательно, новичок работает неритмично.►
следует отвергнуть на данном уровне значимости как не соответствующую опытным данным. Следовательно, новичок работает неритмично.►
Пример 5.1.5. В условиях примера 5.1.4 было получено значение выборочной дисперсии 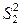 =4, что в два раза превышает эталонное значение
=4, что в два раза превышает эталонное значение 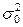 . Это может служить отправной точкой при формулировании альтернативной гипотезы. Действительно, для руководства цеха, где работает новичок, наибольшее опасение должно вызывать то обстоятельство, что дисперсия времени сборки новичком окажется значимо больше эталонного значения. Естественно поэтому переформулировать постановку задачи и проверить основную гипотезу против правосторонней альтернативы. Подтверждается ли опасение руководства на уровне значимости 0,005?
. Это может служить отправной точкой при формулировании альтернативной гипотезы. Действительно, для руководства цеха, где работает новичок, наибольшее опасение должно вызывать то обстоятельство, что дисперсия времени сборки новичком окажется значимо больше эталонного значения. Естественно поэтому переформулировать постановку задачи и проверить основную гипотезу против правосторонней альтернативы. Подтверждается ли опасение руководства на уровне значимости 0,005?
Ответ: нет, не подтверждается.
Пример 5.1.6. Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2 мкм2. Исправленная выборочная дисперсия, найденная по выборке объема 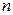 =121, оказалась равной 0,3 мкм2. Можно ли принять партию
=121, оказалась равной 0,3 мкм2. Можно ли принять партию
а) на уровне значимости 1%?
б) на уровне значимости 0,1%?
◄ 1) Гипотезы формулируются аналогично примеру 5.1.5 при эталонном значении 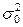 =0,2. Основное отличие заключается в том, что число степеней свободы достаточно велико и соответствующие квантили отсутствуют в таблице. В этом случае следует использовать асимптотическую нормальность распределения хи-квадрат. Как показано в параграфе 4.4 стандартизованная величина
=0,2. Основное отличие заключается в том, что число степеней свободы достаточно велико и соответствующие квантили отсутствуют в таблице. В этом случае следует использовать асимптотическую нормальность распределения хи-квадрат. Как показано в параграфе 4.4 стандартизованная величина
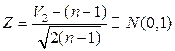 при достаточно больших
при достаточно больших 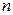 .
.
Отсюда выводится формула (4.4.1), связывающая приближенно квантиль из распределения хи-квадрат с 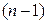 степенями свободы через нормальную квантиль:
степенями свободы через нормальную квантиль:
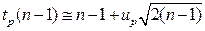 , (5.1.4)
, (5.1.4)
где 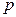 порядок квантили, а
порядок квантили, а 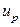 - квантиль порядка
- квантиль порядка 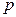 из распределения
из распределения 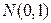 . В нашем случае имеем:
. В нашем случае имеем: 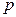 =1
=1 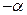 =0,99;
=0,99; 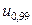 =2,326; Далее по формуле (5.1.4) получаем:
=2,326; Далее по формуле (5.1.4) получаем: 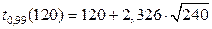 =156,03. Таким образом, критическая область
=156,03. Таким образом, критическая область 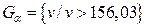 . Находим выборочное значение статистики:
. Находим выборочное значение статистики: 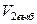 =180
=180 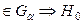 - отклоняется на данном уровне значимости. Партию принять нельзя.
- отклоняется на данном уровне значимости. Партию принять нельзя.
2) Ответ: нельзя.►
Пример 5.1.7. Конкретизируем данные в примере 5.1.2, где обсуждался конфликт между поставщиком и заказчиком. Пусть вероятность получить бракованную деталь в большой партии деталей согласно договору равна 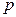 =0,03 (эталонное значение). Заказчик утверждает, что по его данным
=0,03 (эталонное значение). Заказчик утверждает, что по его данным 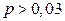 . Для разрешения конфликта было обследовано 400 наудачу отобранных деталей и обнаружено, что 16 из них бракованные. Обе стороны договорились об уровне значимости
. Для разрешения конфликта было обследовано 400 наудачу отобранных деталей и обнаружено, что 16 из них бракованные. Обе стороны договорились об уровне значимости  =0,05. Ответить на следующие вопросы:
=0,05. Ответить на следующие вопросы:
1) Чью гипотезу подтверждает эксперимент?
2) Какова вероятность принять партию, в которой в действительности имеется 6% бракованных деталей?
◄ 1) Проверяется основная гипотеза 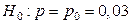 против правосторонней альтернативы
против правосторонней альтернативы 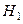 . Подходящей статистикой является
. Подходящей статистикой является
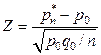 , которая при достаточно больших значениях
, которая при достаточно больших значениях 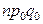 приближенно подчиняется закону
приближенно подчиняется закону 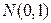 (см. параграф 4.4). Статистику
(см. параграф 4.4). Статистику 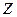 легко преобразовать к виду
легко преобразовать к виду
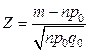 , где
, где 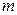 - число бракованных деталей в отобранной партии. В силу выбранной альтернативы, критическая область
- число бракованных деталей в отобранной партии. В силу выбранной альтернативы, критическая область 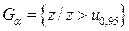 , где
, где 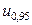 =1,65 из таблицы квантилей нормального распределения. Вычисляем выборочное значение статистики
=1,65 из таблицы квантилей нормального распределения. Вычисляем выборочное значение статистики
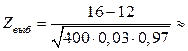 1,172.
1,172.
Так как 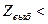 1,65, то нет оснований отвергать гипотезу
1,65, то нет оснований отвергать гипотезу  : выборочные данные не противоречат утверждению поставщика.
: выборочные данные не противоречат утверждению поставщика.
2) Для ответа на поставленный вопрос заметим, что если верна альтернатива 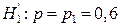 , то число
, то число 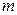 бракованных деталей из 400 распределено по закону
бракованных деталей из 400 распределено по закону 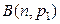 , поэтому
, поэтому
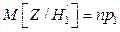 =24,
=24, 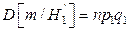 =22,56.
=22,56.
Используя свойства операторов математического ожидания и дисперсии, получаем
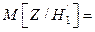 3,52,
3,52, 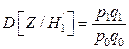 =1,94.
=1,94.
Таким образом статистика 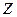 при условии, что
при условии, что 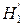 верна, распределена по нормальному закону с параметрами
верна, распределена по нормальному закону с параметрами 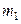 =3,52 и
=3,52 и 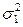 =1,94.
=1,94.
Вероятность принять партию, в которой содержится 6% брака, равна
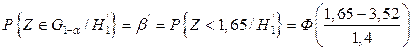 =
=
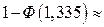 0,091, что почти в два раза больше, чем ошибка первого рода, равная
0,091, что почти в два раза больше, чем ошибка первого рода, равная  =0,05.►
=0,05.►
Комментарий. В пункте 2) предыдущей задачи была найдена ошибка второго рода в ситуации, когда альтернатива точно определяет значение проверяемого параметра. Другими словами, гипотеза 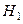 - простая. В случае сложной альтернативы вычислить точное значение ошибки второго рода не представляется возможным. Имеется только уверенность в том, что эта ошибка минимизирована, благодаря оптимизации выбора критической области. Иногда для получения более полной информации об ошибках второго рода (и соответственно мощности критерия) вводится так называемая функция мощности критерия:
- простая. В случае сложной альтернативы вычислить точное значение ошибки второго рода не представляется возможным. Имеется только уверенность в том, что эта ошибка минимизирована, благодаря оптимизации выбора критической области. Иногда для получения более полной информации об ошибках второго рода (и соответственно мощности критерия) вводится так называемая функция мощности критерия: 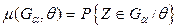 и исследуется как функция от
и исследуется как функция от 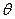 . Однако это несколько выходит за рамки нашей программы. Интересующимся предлагаем обратиться к соответствующей литературе [5].
. Однако это несколько выходит за рамки нашей программы. Интересующимся предлагаем обратиться к соответствующей литературе [5].
 2015-10-13
2015-10-13 4257
4257








