2015-10-14
659
Функция y =f(x) называется непрерывной в точки, если:
1) она определена в этой точке;
2) существует предел lim f(х);
3) этот предел равен значению функции в точке х0 т. е.
 |
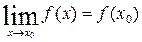Вопросы для самоподготовки:
1. Дайте определение математическому понятию «функция».
2. Какими способами задается функция?
3. Какими свойствами обладает функция, охарактеризуйте каждый и способов.
4. Приведите классификацию функций и их графиков.
5. Приведите примеры четных и нечетных функций, периодических, ограниченных и неограниченных, непрерывных и имеющих точки разрыва.
6. Дайте определение математическому понятию «предел функции».
7. Какая функция называется непрерывной?
8. Какими свойствами обладает непрерывная функция?
9. Дать понятие точки разрыва?
Тест для самоконтроля:
1. Нули функции-это те точки, в которых функция пересекает:
a) ось абсцисс
b) ось ординат
c) начало координат
2. График функции и расположение на координатной плоскости:
| 1) четная | a) симметрична относительна оси Х |
| 2) нечетная | b) симметрична относительно оси У c) симметрична относительно начала координат |
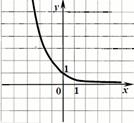
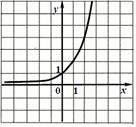
3. График функции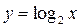 
|
|
|
| 
| 
| 
|
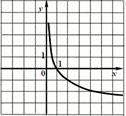
| a) | b) | c) | d) |
4.Подпишите название графика:
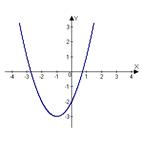
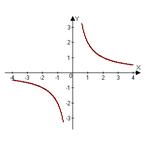
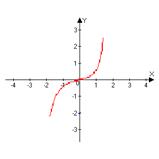
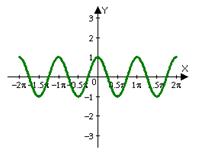
5. График периодической функции:
| 
|
| 
|
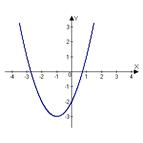
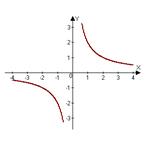
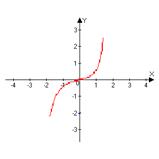
| a) | b) | c) | d) |
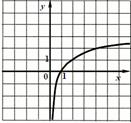
6. График четной функции:
|
| 
|
| 
|
| a) | b) | c) | d) |
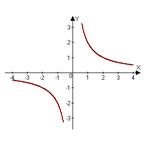
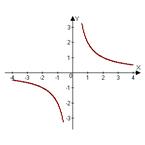
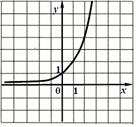
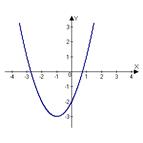
7. График нечетной функции:
| 
| 
| 
|
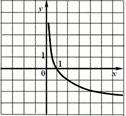
| a) | b) | c) | d) |
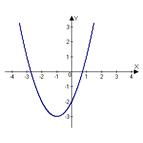
8. График функции, ограниченной сверху и снизу:
|
|
|
|
| a) | b) | c) | d) |
9. Все значения, которые принимает независимая переменная, образуют область....
a) определения функции
b) значений функции
c) возрастания функции
d) убывания функции
10. Функция называется......, если f(x-T)=f(x)=f(x+T) (T>0 для любого х):
a) периодической
b) ограниченной
c) возрастающей
d) монотонной
11.Промежуток возрастания функции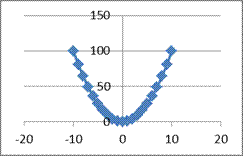 
y=x2
a)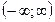 
b)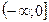 
c)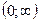 
d)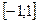 
12.Если для любого х из области определения функции выполняется равенство f(-x)=f(x), то функция называется……
13.Если для любого х из области определения функции выполняется равенство f(-x)=-f(x), то функция называется……..
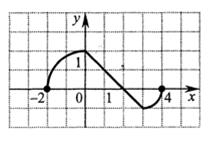
14. Укажите промежуток убывания функции y=f(x), заданной графиком
a) [2;3]
b) [0;3]
c) [2;4]
d) (-1;2)
15. Вычислите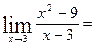 
….
16.Область определения функции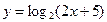 
a)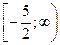 
b)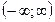
c)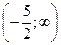 
d)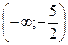 
17. Вычислите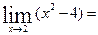 
a)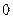 
b)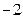 
c)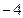 
d)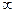 
18. Вычислите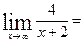 
a)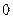
b)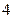 
c)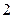 
d)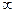
19. Точки разрыва функции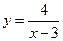 
a) нет точек разрыва
b) x=3
c) x=4
d) x=2
20. Промежутки непрерывности функции
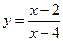
a)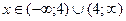 
b)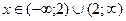 
c)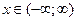 
d)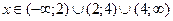 
21. Свойство непрерывности функции нарушается в...
a) точке дифференцирования
b) области определения
c) области интегрирования
d) точке разрыва
22.Вычислите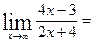 
Ключ для самопроверки теста:
1) a
2) 1b, 2c
3) b
4) Парабола, гипербола, кубическая парабола, косинусоида
5) c
6) a
7) b
8) c
9) a
10) a
|
|
|
11) c
12) четная
13) нечетная
14) b
15) 6
16) c
17) a
18) a
19) b
20) a
21) d
22) 2
Литература:
1. Омельченко В.П., Демидова А.А. Математика: Компьютерные технологии в медицине. – Ростов н/Д:Феникс, 2008. -588 с. Ил.-(Среднее профессиональное образование)
2. Подготовка к ЕГЭ по математике [электронный ресурс]: конспект по алгебре. URL: http://uztest.ru/abstracts/
Производная функции. Дифференциал и его приложение к приближенным вычислениям
Значение темы:
Понятие производной находит многочисленные применения в геометрии, физике, механике, химии, биологии и других науках.
Так как понятие производной связано с изменением за какой-то промежуток времени, то быстрота протекания физических, химических, биологических и других процессов, например, скорость охлаждения тела, скорость химических реакций, всё это также выражается при помощи производной.
На основе теоретических знаний и практических умений обучающийся должен:
знать:
- определение непрерывности и дифференцируемости функции;
- приращение функции, приращение аргумента;
- определение производной ее геометрический и механический смысл;
- таблицу производных;
- определение дифференциала.
уметь :
- находить производные элементарных и сложных функций;
- вычислять дифференциалы функции;
- применение дифференциала к приближённым вычислениям.
Краткое содержание темы:
Производные простейших элементарных функций
| 
|
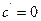
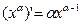
| (ax)’=axlna, в частности (ех)’= ех |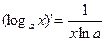 
в частности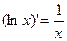 
|
| (sin x)’=cos x | (cos x)’= - sin x |
| 
|
| 
|
| 
|
 |
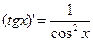
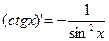
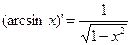
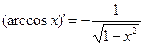
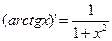
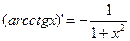
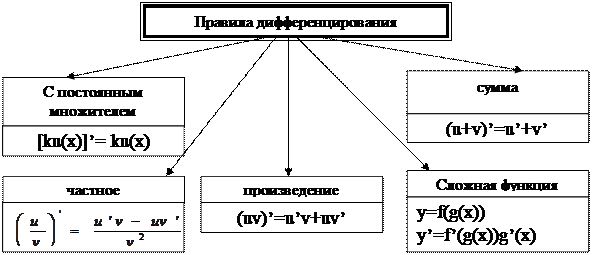Вопросы для самоподготовки:
1. Дайте определение производной.
2. Назовите производные элементарных и сложных функций.
3. Сформулируйте правила вычисления производных суммы, произведения, частного.
4. Дайте определение дифференциала функции.
5. Дифференциал функции в некоторой точке х0 равен нулю при любом приращении аргумента. Что означает это геометрически?
6. Для какой функции её дифференциал совпадает с ее приращением?
Тест для самоконтроля:
1. Функция и её производная:
1) 
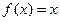
| a)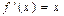 
|
2) 
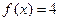
| b)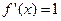 
|
3) 
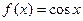
| c)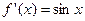 
|
4) 
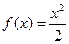
| d)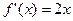 
|
e)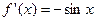 
| |
f)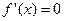 
|
2. Производная функции у=(x-3)·cos x равна...
a) y'=cosx+(x-3)sinx
b) y'=(x-3)sinx-cosx
c) y'=cosx-(x-3)sinx
d) y'=-sinx
3. Дифференцирование -...
a) Процесс вычисления производной
b) Свойство производной
c) Условие вычисления предела
d) Процесс вычисления определенного интеграла
e) Процесс вычисления неопределенного интеграла
f) Свойство тригонометрической функции
4. Соответствие производных:
1) 
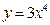
| a)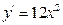 
|
2) 
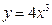
| b)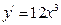 
|
3) 
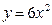
| c)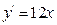 
|
4) 
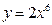
| d)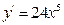 
|
5) 
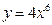
| e)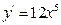 
|
f)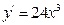 
|
5. Найдите значение y’(2), если y=2x3
a) 24
b) 16
c) 12
d) 10
e) 18
f) 20
6. Соответствие производных
1) 
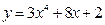
| a)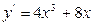 
|
2) 
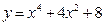
| b)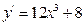 
|
3) 
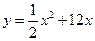
| c)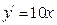 
|
4) 
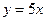
| d)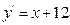 
|
5) 
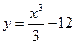
| e)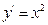 
|
6) 
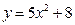
| f)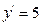 
|
7. Соответствие производных:
1) 
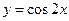
| a)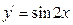 
|
2) 
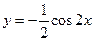
| b)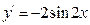 
|
3) 
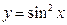
| c)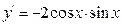 
|
4) 
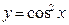
| d)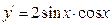 
|
5) 
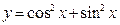
| e) 
|
6) 
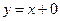
| f) 
|
8. 
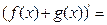
a)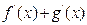 
b)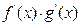 
c)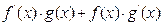 
d)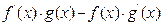 
e)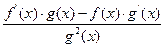 
f)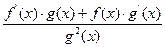 
9. 
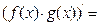
a)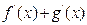
b)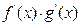
c)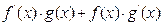
d)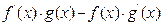
e)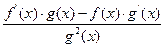
f)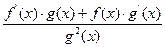
10. 
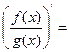
a)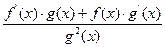
b)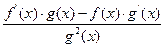
c)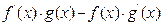
d)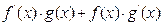
e)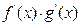
f)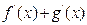
Ключ для самопроверки теста:
1) 1b, 2f, 3c, 4a
2) c
3) a
4) 1b, 2a, 3c, 4e, 5d
5) a
6) 1b, 2a, 3d, 4f, 5e, 6c
7) 1b, 2a, 3d, 4c, 5f, 6e
8) a
9) c
10) b
Литература:
1. Омельченко В.П., Демидова А.А. Математика: Компьютерные технологии в медицине. – Ростов н/Д:Феникс, 2008. -588 с. Ил.-(Среднее профессиональное образование)
2. Подготовка к ЕГЭ по математике [электронный ресурс]: конспект по алгебре. URL: http://uztest.ru/abstracts/
