Уравнения Гельмгольца. Волновой характер электромагнитного поля

Одним из важнейших результатов, полученных Максвеллом, явилось доказательство волновой природы электромагнитного поля. Уже упоминалось о том, что изменение во времени электрического поля приводит к возникновению магнитного поля, неоднородного в пространстве, и наоборот. Физическая картина здесь напоминает процесс обмена энергией между электрическим и магнитным полем в обычном колебательном контуре. Поэтому можно ожидать, что электромагнитный процесс в самом общем случае представляет собой также некоторые колебания. Принципиальная разница здесь заключается в том, что колебания электромагнитного поля должны рассматриваться одновременно во всех точках пространства. В физике колебательное движение непрерывной среды принято называть волновым процессом.

Докажем волновой характер электромагнитного поля математически, сведя уравнения Максвелла к другим уравнениям, которые заведомо описывают волновой процесс.

Рассмотрим электромагнитное поле в некоторой области пространства, где плотность зарядов отсутствует, т.е. 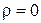. Плотность сторонних электрических токов также предполагается равной нулю.

Выпишем первые два уравнения из общей системы уравнений Максвелла для комплексных амплитуд в виде:

Эти два уравнения могут быть сведены к одному. Для этого применим операцию rot к левой и правой частям второго уравнения, а затем выразим полученную правую часть через второе уравнение:

Здесь − в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величины можно встретить также названия фазовая постоянная или волновое число.

Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождеством векторного анализа:

.

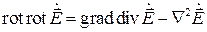Здесь (набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие оператора сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа

.

Если воспользоваться законом Гаусса, который в соответствии с принятым условием 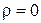обеспечивает , то уравнение может быть переписано в следующем простом виде:

Пользуясь симметрией уравнений Максвелла, совершенно аналогично получаем также уравнение относительно векторного поля :

.

Эти два уравнения в математической физике носят название уравнений Гельмгольца. Математически можно показать, что эти уравнения описывают стационарные волновые процессы, т.е., распространение в пространстве волн с некоторой постоянной частотой.

Таким образом, получен фундаментальный вывод теории Максвелла − переменность во времени электрических или магнитных полей приводит к распространению в пространстве электромагнитных волн.

В координатной форме уравнения Гельмгольца записываются следующим образом

или

.

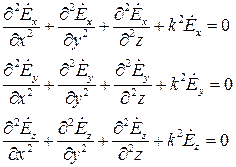Решение такой системы значительно упрощается в тех частных случаях, когда поле не имеет каких-либо составляющих, например, , а также тогда, когда поле постоянно в каких-либо плоскостях, например .

Волновые процессы

Как уже указывалось, переменное во времени электромагнитное поле носит волновой характер. Далее мы рассмотрим волновые процессы, происходящие в электромагнитном поле.

С самой общей точки зрения волнами называются колебательные движения непрерывных сред. Физическая природа волновых явлений чрезвычайно разнообразна. Так, известны электромагнитные волны, звуковые – акустические волны, волны на поверхности жидкости и т.д. Проведение всеобъемлющей классификации здесь весьма затруднительно. Для понимания структуры электромагнитных волн сравним между собой два хорошо известных и легко представимых волновых процесса − звуковые волны и волны на поверхности воды (рисунок 41).

Рисунок 41 − Продольные и поперечные волны

Волны, показанные на рисунке, распространяются в направлении стрелок. Звуковые волны, представляющие собой перемещение в пространстве областей сгущения и разрежения газа, характеры тем, что в них каждая отдельная частица газа колеблется в направлении, совпадающем с направлением распространения волны. Такие волны носят название продольных волн. В литературе можно встретить также термины акустические или скалярные волны.

Совсем иной природой обладают волны на поверхности воды. Здесь колеблющиеся частицы перемещаются в направлении, перпендикулярном направлению распространения. Поэтому для волны данного вида недостаточно лишь указать величину смещения колеблющихся точек относительно положения равновесия, а следует указать конкретно ту плоскость, в которой происходят колебания. Эта плоскость называется плоскостью поляризации волны, а сам волновой процесс – поперечными, поляризованными или векторными волнами.

Можно доказать, и это будет видно из примеров, что электромагнитные волны имеют вид поперечных волн. Волны разной физической природы классифицируются в зависимости от того, какую конфигурацию они принимают в пространстве.

Плоские волны

Рассмотрим безграничное трехмерное пространство с декартовой системой координат, в каждой точке которого задана некоторая величина , физическая природа которой безразлична. Пусть эта величина во времени и пространстве изменяется по закону

.

При этом говорят, что в пространстве существует монохроматическая плоская волна. Аргумент косинуса, т.е. , называемый обычно фазой волны, является функцией времени и пространственной координаты . Если зафиксировать , то величина принимает те же самые значения через промежутки времени, кратные периоду . Если же фиксировано время, то величина изменяется периодически вдоль оси с периодом , называемом длиной волны. Легко видеть, что величины и связаны друг с другом:

.

Величина служит важнейшей характеристикой волнового процесса и носит название постоянной распространения волны. Употребляются также термины фазовая постоянная и волновое число, а вместо символа используется . Физический смысл волнового числа состоит в том, что оно указывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.

Наличие двух возможных знаков в формуле, описывающей плоскую волну, связано с тем, что плоские волны могут распространяться в двух направлениях. Назовем поверхность, удовлетворяющую условию

,

волновым фронтом плоской волны. Очевидно, что в рассматриваемом случае волновые фронты представляют собой бесконечные плоскости, перпендикулярные оси и перемещающиеся в пространстве со скоростью

,

носящей название фазовой скорости. Фазовая скорость − это скорость, с которой должна перемещаться точка наблюдения, чтобы фаза поля в ней оставалась неизменной. Поскольку время изменяется всегда в одном направлении, то уравнение

соответствует фронту волны, распространяющейся в направлении положительной оси . Изменение знака в фазе волны ведет к изменению направления ее распространения.

Рисунок 42 − Плоская волна

Введем комплексные амплитуды плоских волн. В соответствии с методом комплексных амплитуд будем иметь для волны, распространяющейся в положительном направлении

,

а для волны, идущей в противоположную сторону,

.

Распространение волн в любой реальной среде неизбежно сопровождается уменьшением их амплитуды за счет тепловых потерь. Закон затухания легко найти из следующих простых соображений. Предположим, что в начальной плоскости амплитуда волны имеет исходную величину , условно принимаемую за 100%. Положим далее, что при прохождении 1 м пути амплитуда падает на 10%, т.е. . Легко найти, что , и т.д. Общая закономерность имеет вид

Из алгебры известно, что именно таким свойством обладает показательная функция, т.е. в общем виде можно записать соотношение пропорциональности

.

Рисунок 43 − Спадание амплитуды волны при распространении в среде с потерями

Здесь носит название постоянной затухания волны. Величины и можно объединить, введя комплексную постоянную распространения :

.

Итак, вещественная часть определяет закон изменения фазы в распространяющейся волне, в то время как мнимая часть характеризует затухание.

Сферические волны

Данный тип волн получается в тех случаях, когда какой-либо точечный источник возбуждает неограниченное однородное пространство. В силу полной симметрии задачи волновые фронты имеют вид сфер. Если ограничиться простейшим случаем, когда амплитуда колебаний зависит лишь от радиальной координаты , то можно показать, что при гармоническом законе изменения поля во времени справедлива следующая зависимость:

,

или, если выразить величину 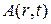через ее комплексную амплитуду,

Рисунок 44 − Сферическая волна

Сферические волны являются важным объектом изучения в электродинамике, поскольку с ними связаны многие задачи об излучении антенн.

Цилиндрические волны

Волны, возбуждаемые бесконечной нитью источников, расположенных вдоль оси , носят название цилиндрических волн. Волновые фронты при этом имеют вид коаксиальных цилиндров. Можно показать, что на расстоянии от оси, значительно превышающем длину волны, справедливо следующее приближенное равенство:

Рисунок 45 − Цилиндрическая волна

Цилиндрические волны рассматриваются в задачах электродинамики, связанных с излучением электромагнитных волн отрезками линейных проводников.