Проверка гипотез о равенстве средних двух и более совокупностей

Сравнение средних двух совокупностей имеет важное практическое значение. На практике часто встречается случай, когда средний результат одной серии экспериментов отличается от среднего результата другой серии. При этом возникает вопрос, можно ли объяснить обнаруженное расхождение средних неизбежными случайными ошибками эксперимента или оно вызвано некоторыми закономерностями. В промышленности задача сравнения средних часто возникает при выборочном контроле качества изделий, изготовленных на разных установках или при различных технологических режимах в финансовом анализе – при составлении уровня доходности различных активов.

Сформулируем задачу. Пусть имеются две совокупности, характеризуемые генеральными средними и и известными дисперсиями и . Необходимо проверить гипотезу о равенстве генеральных средних, то есть . Для проверки гипотезы из этих совокупностей взяты две независимые выборки объемов n₁ и n₂, по которым найдены средние арифметические и и выборочные дисперсии и .

Статистическим критерием для проверки этой гипотезы является нормированная нормально распределенная случайная величина

Вид критической области зависит от типа конкурирующей гипотезы:

а) Н ₁: – критическая область двусторонняя, t_кр определяется как аргумент функции Лапласа, при котором . Если фактически наблюдаемое значение статистики t больше t_кр, определенного на уровне значимости 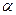(по абсолютной величине), то есть > t_кр, то делается вывод, что нулевая гипотеза H₀ не противоречит имеющимся наблюдениям.

б) Н ₁: (Н ₁: ) критическая область правосторонняя (левосторонняя), t_кр определяется как аргумент функции Лапласа, при котором . Если фактически наблюдаемое значение статистики t больше t_кр, определенного на уровне значимости 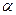(по абсолютной величине), то есть > t_кр, то делается вывод, что нулевая гипотеза H₀ не противоречит имеющимся наблюдениям.

Будем теперь предполагать, что распределение признака (случайной величины) Х и У в каждой совокупности имеет нормальный закон. В этом случае, если дисперсии и известны, то проверка гипотезы проводится так же, как описано выше. Если дисперсии и неизвестны, но равны, = = , то в качестве неизвестной величины можно взять ее оценку – «исправленную» выборочную дисперсию. Однако «лучшей» оценкой для будет дисперсия «смешанной» совокупности объема n₁₊n₂. В случае справедливости гипотезы H₀ статистика:

имеет t-распределение Стьюдента с степенями свободы. Критическое значение статистики находится в зависимости от типа критической области, в которых вместо функции Лапласа Ф(t) берется функция для распределения Стьюдента при числе степеней свободы , то есть или .

Сохраняется то же правило опровержения (принятия) гипотезы: гипотеза H₀ отвергается на уровне значимости 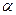, если (в случае односторонней критической области), либо если (в случае двусторонней критической области); в противном случае гипотеза H₀ не отвергается (принимается).

Таким образом, критерии проверки гипотез о равенстве средних двух или более совокупностей можно представить в виде таблицы.

Нулевая гипотеза	Предполо-жения	Статистика критерия	Альтернативная гипотеза	Критерий отклонения гипотезы
	известна
	неизвестна