2015-10-22
1125
Этот метод также рассмотрим в дальнейшем на примере.
Пример 3.1. Дана система 3-го порядка. Решить систему:
а) Методом Крамера (по формулам Крамера);
б) С помощью обратной матрицы (матричным методом).
1). 
а) Решаем по формулам Крамера. Найдем:
,
значит система имеет единственное решение, которое найдем по формулам Крамера:
; 
; 
.
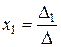Составим определители для неизвестных и найдем их:
;
; 
; 
.
Проверка. Подставим найденные значения в исходную систему:
б) Решим систему матричным методом.
Решением будет 
.
Найдем обратную матрицу по формуле 
.
- согласно предыдущему способу. Составим 
, для этого найдем алгебраические дополнения:
 ;
|  ;
|  ;
|
 ;
|  ;
|  ;
|
 ;
|  ;
|  .
|
Ответ: 
; 
; 
.
2). 
Найдем определитель системы:
Так как система неоднородная и 
, то система несовместна (не имеет решения).
3). 
Найдем определитель системы:
Определители для неизвестных 
, так как имеют нулевой столбик. Значит система совместна и определена, имеет единственное нулевое решение:
|
|
|
4). 
Найдем определитель системы:
Система совместна и неопределена, так как она однородная. Запишем систему в виде:
- уберем второе уравнение (убирать можно любое).
Далее запишем:
Решим методом Крамера:
Итак 
- общее решение,
где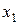 
и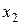 
- зависимые переменные;
- независимая переменная.
Найдем частное решение. Т.е. положим 
.
Получим: 
.
Сделаем проверку:
- верно.
Задание 3.1. Решить системы линейных алгебраических уравнений
а) Методом Крамера (по формулам Крамера);
б) С помощью обратных матриц.
Сделать проверку.
№1.
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10.  ;
|
11.  ;
| 12.  ;
|
13.  ;
| 14.  ;
|
15.  ;
| 16.  ;
|
17.  ;
| 18.  ;
|
19.  ;
| 20.  ;
|
21.  ;
| 22.  ;
|
23.  ;
| 24.  ;
|
25.  ;
| 26.  ;
|
27.  ;
| 28.  ;
|
29.  ;
| 30.  .
|
№2.
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10.  ;
|
11.  ;
| 12.  ;
|
13.  ;
| 14.  ;
|
15.  ;
| 16.  ;
|
17.  ;
| 18.  ;
|
19.  ;
| 20.  ;
|
21.  ;
| 22.  ;
|
23.  ;
| 24.  ;
|
25.  ;
| 26.  ;
|
27.  ;
| 28.  ;
|
29.  ;
| 30.  .
|
№3.
1.  ;
| 2. ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10.  ;
|
11.  ;
| 12.  ;
|
13.  ;
| 14.  ;
|
15.  ;
| 16.  ;
|
17.  ;
| 18.  ;
|
19.  ;
| 20.  ;
|
21.  ;
| 22.  ;
|
23.  ;
| 24.  ;
|
25.  ;
| 26.  ;
|
27.  ;
| 28.  ;
|
29.  ;
| 30.  .
|
№4.
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5.  ;
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10.  ;
|
11.  ;
| 12.  ;
|
13.  ;
| 14.  ;
|
15.  ;
| 16.  ;
|
17.  ;
| 18.  ;
|
19.  ;
| 20.  ;
|
21.  ;
| 22.  ;
|
23.  ;
| 24.  ;
|
25.  ;
| 26.  ;
|
27.  ;
| 28.  ;
|
29.  ;
| 30.  .
|
Пример 3.1. Дана система линейных алгебраических уравнений.
Решить ее:
А) методом Гаусса
б) методом Жордана-Гаусса.
Решение:
а) Решаем методом Гаусса. Запишем расширенную матрицу системы:
1шаг:
Элементы первой строки умножаем на 2 и сложим с соответствующими элементами 2-й строки, затем элемент 1-й строки умножим на 3 и сложим с 3-й строкой, умножим на 4 и сложим с 4-й строкой. Получим эквивалентную матрицу:
|
|
|
~ 
~
2 шаг.
Поменяем местами 2-й и 4-й столбцы, отметим, в эквивалентной матрице какой переменной соответствуют столбцы.
~ 
~
Шаг.
Умножим элементы 2-й строки на (-1) и сложим с элементами 3-й и 4-й строк.
~ 
~
Шаг.
Поменяем местами 3-ю и 4-ю строки
~ 
теперь уже точно система приведена к треугольному виду.
Обратный ход:
Проверка. Подставим найденные значения в исходную систему.
получим тождества
Ответ: 
