Нестационарная теплопроводность

1 2 3 4 5 6 7

5.1. Бесконечная пластина с граничными условиями третьего рода

Рис. 22. Нестационарная теплопроводность пластины

Рассмотрим процесс нагрева (охлаждения) бесконечной пластины толщиной 2

с начальной температурой

. Поместим пластину в среду с температурой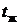

, которая остаётся постоянной за время процесса. Коэффициент теплоотдачи с обеих сторон пластины одинаков и не изменяется с течением времени. Теплофизические свойства пластины не зависят от температуры. Температурное поле в пластине описывается уравнением теплопроводности

. Начальное условие запишем в виде

При принятых условиях осуществления процесса нагрева (охлаждения) поле температур в пластине будет симметрично относительно её середины. Поместим начало координат в центр пластины и одно из граничных условий зададим в виде условия симметрии

Второе граничное условие зададим на поверхности пластины

Введём в задачу вместо температуры t избыточную температуру . Получим

;

Приведём задачу к безразмерному виду. В качестве масштаба измерения линейных размеров примем половину толщины пластины , а в качестве масштаба измерения избыточной температуры – . Таким образом определим безразмерную координату , а безразмерную избыточную температуру как .Выразим размерные величины через безразмерные и подставим в задачу.

; .

или .

Выражение безразмерно и называется числом Фурье, которое можно рассматривать как безразмерное время. Уравнение теплопроводности в безразмерном виде имеет вид

. (5.1)

Начальное условие в безразмерном виде

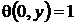. (5.2)

Граничное условие в центре пластины в безразмерном виде

. (5.3)

Граничное условие на поверхности в безразмерном виде

. (5.4)

где называется критерием подобия Био.

Решение уравнения (5.1) ищем методом разделения переменных Фурье – в виде произведения двух функций, одна из которых зависит только числа Фурье, а вторая – только от координаты y.

. (5.5)

Подставим (5.5) в уравнение (5.1).

или

Откуда получим два обыкновенных дифференциальных уравнения

;

Решение первого уравнения есть

Решение второго уравнения есть

Таким образом, общее решение уравнения (5.1) имеет следующий вид:

или

. (5.6)

Для определения постоянных А, В и k имеется три условия (5.2) – (5.4). Условие симметрии (5.3) означает, что решение (5.6) должно быть чётной функцией у. Следовательно, в нём не должно быть нечётной функции . А это означает, что постоянная B должна быть равна нулю, В =0. Таким образом, решение (5.6) преобразуется к виду

. (5.7)

Используем граничное условие (5.4). Получим условие

которое преобразуется к виду

. (5.8)

Уравнение (5.8) называется характеристическим уравнением.

Рис. 23. К решению уравнения (5.8)

На рис. 23 представлены графики левой и правой частей (5.8). Точки пересечения котангенсоид с линией

и есть корни характеристического уравнения (5.8). Таким образом, уравнение (5.8) имеет бесконечное множество корней, каждому из которых соответствует частное решение

. Общее решение дифференциального уравнения будет равно сумме всех частных решений, т.е.

. (5.9)

Постоянные найдём из начального условия. Если (5.9) есть решение дифференциального уравнения, то оно должно описывать также и стационарное состояние, определяемое начальным условием (5.2). При Fo=0 получим

Умножим полученное равенство на и проинтегрируем по y от –1 до +1.

Известно, что . Таким образом, для каждого значения получим

откуда найдём .

Окончательно, решение задачи имеет следующий вид

. (5.10)

Заменив безразмерные переменные на размерные, получим решение в следующем виде

Анализ решения

Из рис. 23 видно, что корни характеристического уравнения представляют собой ряд возрастающих чисел, поэтому вклад очередного члена ряда (5.10) меньше предыдущего. Кроме того, чем больше критерий Фурье, тем быстрее сходится ряд. Исследования показывают, что уже при ряд становится настолько быстросходящимся, что распределение температуры в пластине достаточно точно описывается первым членом ряда.

. (5.11)

Обозначим . Эта функция зависит только от числа Био, поэтому её можно вычислить и затабулировать. Решение (5.11) можно записать в виде

. (5.12)

На поверхности пластины y =1 и решение (5.12) можно записать в виде

где . В центре пластины

где . Функции и содержатся в таблицах. Рассмотрим три случая изменения температуры в теле.

1) Случай, когда (практически )

Если , то температура поверхности пластины становится равной температуре окружающей среды. Это возможно, когда , т.е. имеет место очень большая интенсивность отвода тепла от поверхности. Процесс нагрева (охлаждения) определяется только физическими свойствами и размерами тела и не зависит от условий теплообмена на поверхности. При этом и коэффициент ряда

Решение для данного случая принимает вид

Рис. 24. Распределение температуры в пластине при различных числах Bi

Распределение температуры в пластине в этом случае представлено на рис. 24а.

2). Очень малые числа Bi (практически Bi < 0,1 ).

При Bi все члены ряда кроме , который равен

При малых и и характеристическое уравнение преобразуется к виду . В результате решение принимает вид

При y =0 ; при y =1 .

Отношение температур на оси и поверхности есть

и при Bi стремится к 1. Таким образом, температуры на поверхности и в центре пластины практически одинаковы. Распределение температуры по толщине пластины в этом случае показано на рис. 24б.