Теоретичні відомості про математичні показники надійності

11.2.1. Математичне сподівання (середнє значення) 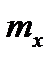– основна і найпростіша характеристика випадкової величини X. Значення математичного сподівання, що визначається за результатами спостережень, для дискретних і безперервних величин називають оцінкою математичного сподівання, або оцінкою середнього значення :

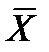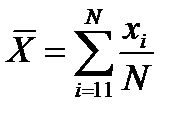, або ,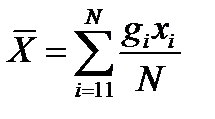

де х_і – поточне значення випадкової величини; g_i – кількість однакових значень х_і; N – загальна кількість спостережень.

У першій формулі складають усі N членів, у другій – кількість членів з різними значеннями х_і. За досить великої кількості спостережень вважають, що m_x = 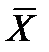. В імовірнісних задачах математичне сподівання визначають залежно від щільності розподілу f(x) (для безперервних величин) або ймовірності p_і появи значення х_і (для дискретних величин):

; .

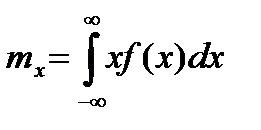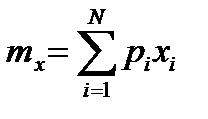11.2.2. Мода – значення випадкової величини, що трапляється найчастіше, або найбільш імовірне її значення.

11.2.3. Квантиль– значення випадкової величини, що відповідає заданій імовірності. Квантиль, що відповідає імовірності 0,5, називають медіаною.

11.2.4. Медіанає центром групування випадкової величини. Площу під графіком медіана поділяє навпіл.

Для нормального закону розподілу випадкових величин, який описує відома крива Гаусса, математичне сподівання, мода і медіана збігаються.

11.2.5. Дисперсія випадкової величини – це математичне сподівання квадрату відхилення цієї величини від її математичного сподівання.

Оцінка дисперсії випадкової величини – середнє значення квадрата різниці між значеннями випадкової величини та її середнім значенням:

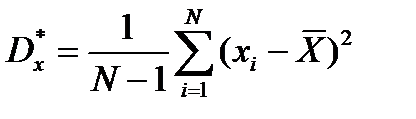, або ,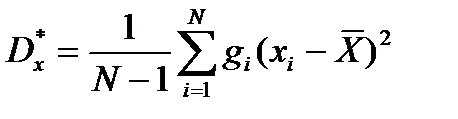

де N – загальна кількість спостережень; х_і – поточне значення випадкової величини; 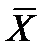– середнє значення випадкової величини; g_i – кількість однакових значень випадкової величини.

Поняття “дисперсія ” означає розсіювання і характеризує розбіжність випадкової величини.

Для безперервних випадкових величин

.

 

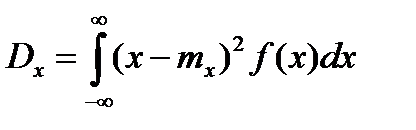Для дискретних випадкових величин

,

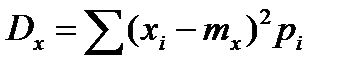де p_і – імовірність появи значення .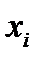

Дисперсія вимірюється квадратом розмірності випадкової величини. Оскільки зручніше користуватися характеристикою розсіювання, що має розмірність випадкової величини, введено характеристику середнє квадратичне відхилення, тобто квадратний корінь з дисперсії:

.

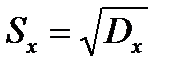Для оцінювання розсіювання випадкових величин за допомогою безрозмірної (відносної) характеристики використовують коефіцієнт варіації,що дорівнює відношенню середнього квадратичного відхилення до математичного сподівання:

.

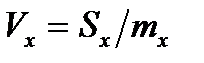Порядок виконання

1. Відповідно до табличних даних, визначених в табл. 10.2. розрахувати математичне сподівання, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

2. Для визначених в практичному занятті 10 закону розподілу побудувати графічні залежності , , .

3. Для самостійної роботи рекомендується додатково вирішити задачі, наведені в додатку 11 в таблиці Д.11.1.

Приклад виконання.

Розрахуємо математичні характеристики закону розподілу закону розподілу (практична робота 10) з врахуванням даних табл. 10.1

Математичне сподівання оцінюємо за формулою

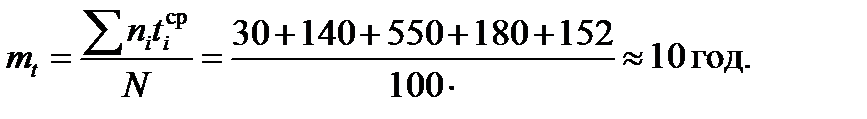
Дисперсію оцінюємо за формулою

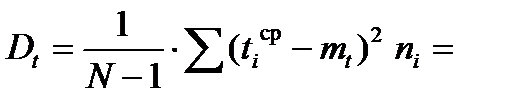
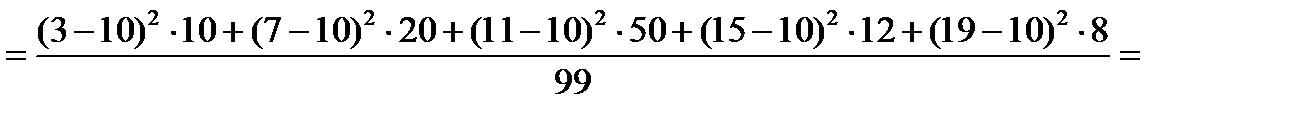
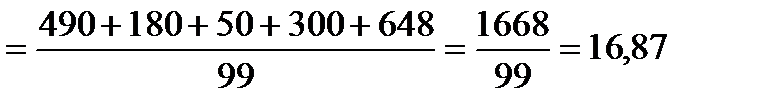
Середньоквадратичне відхилення

.

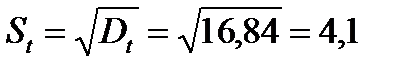Коефіцієнт варіації

.

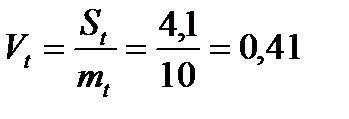За результатами розрахунків, наведених в табл.10.1 будуємо графічні залежності показників надійності колінчастого вала холодильного компресора.

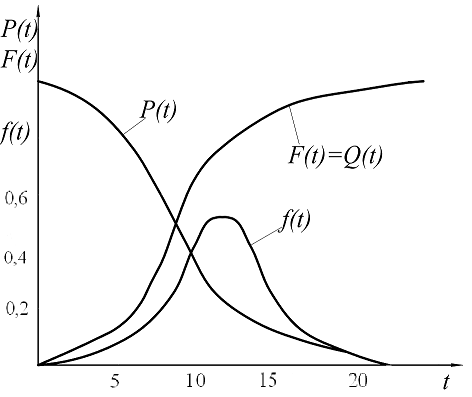
Рис. 11.1. Показники надійності колінчастого вала холодильного компресора: – імовірність безвідмовної роботи; – імовірність відмови; – функція щільності розподілу випадкової величини

11.4. Контрольні запитання

1) Як розраховується математичне сподівання та його зв'язок з оцінкою середнього значення .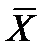

2) Що таке дисперсія і що вона означає?

3) Яка особливість розрахунку дисперсії для безперервних та дискретних величин?

4) З якою метою вводиться показник середнього квадратичного відхилення?

5) Як пов’язані між собою характеристики графічних залежностей P(t) та F(t).