2017-12-14
1578
Значительное повышение точности приближенных формул численного интегрирования дает метод парабол (Симпсона). Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = f(x), чем хорда, соединяющая концы дуги этой кривой (метод трапеций). Поэтому значения площадей соответствующих элементарных трапеций, ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y = f(x), чем значения площадей соответствующих прямолинейных трапеций.
Рассмотрим функцию y = f(x). Будем считать, что на отрезке [ a; b ] она положительна и непрерывна. Найдем площадь криволинейной трапеции aABb (рис. 20).
Для этого разделим отрезок [ a, b ] точкойc =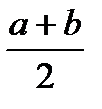 
пополам и в точке C (c, f (c)) проведем касательную к линии y = f(x). После этого разделим [ a, b ] точками p и q на три равные части и проведем через них прямые x = p и x = q. Пусть P и Q – точки пересечения этих прямых с касательной. Соединив A с P и B с Q, получим три прямолинейные трапеции aAPp, pPQq, qQBb. Тогда площадь трапеции aABb можно приближенно посчитать по следующей формуле
,
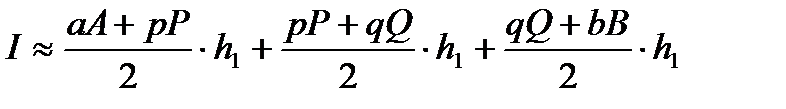где 
.
Откуда получаем
.
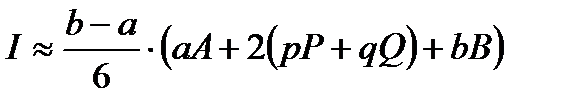| O |
| x |
| y |
| y = f(x) |
| a |
| A |
| p |
| b |
| c |
| B |
| q |
| P |
| C |
| Q |
| h1 |
| h1 |
Рисунок 20 – Геометрическая интерпретация метода парабол
Заметим, что aA = f (a), bB = f (b),а pP + qQ =2 f (c) (как средняя линия трапеции), в итоге получаем малую формулу Симпсона
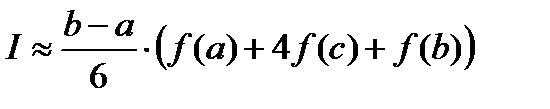(8)
В данном случае дуга ACB заменяется параболой, проходящей через точки A, P, Q, B.
Малая формула Симпсона дает интеграл с хорошей точностью, когда график подынтегральной функции мало изогнут, в случаях же, когда дана более сложная функция, малая формула Симпсона непригодна. Тогда, чтобы посчитать интеграл заданной функции нужно разбить отрезок [ a, b ] на n частей и к каждому из отрезков применить формулу (8).
Обязательным требованием, вытекающим из геометрического смысла метода парабол, является то, что n должно быть четным. Пусть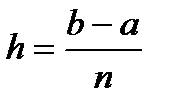 
, точки деления будут х 0 =а, x 1, x 2, …xn- 2, xn- 1, xn=b, а y 0, y 1, …yn – соответствующие значения подынтегральной функции на отрезке [ a, b ].
Тогда, применяя малую формулу Симпсона к каждой паре получившихся отрезков, имеем
Тогда
. (9)
Заметим, что во всех выражениях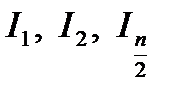 
первый множитель равен 
:
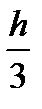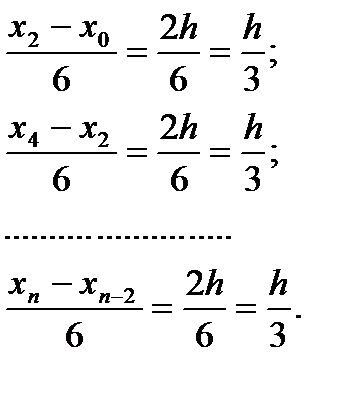(10)
Сделав замену по формулам (10), вынося общий множитель 
за скобку, в (9) получаем:
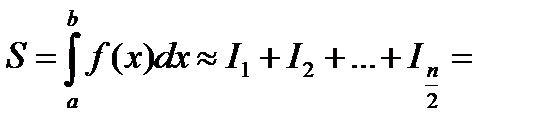
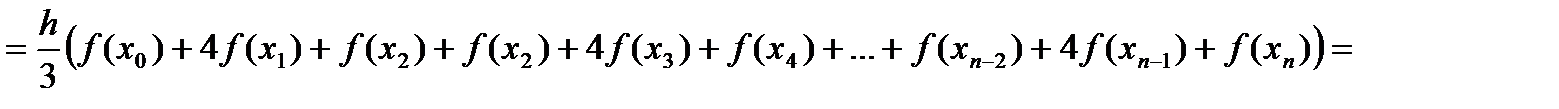
группируем слагаемые
.
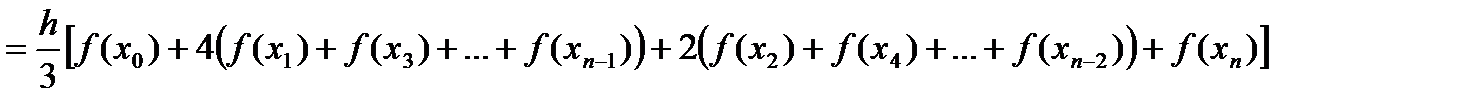Таким образом, получаем «большую» формулу Симпсона, которая имеет вид:
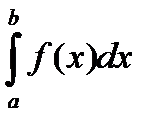
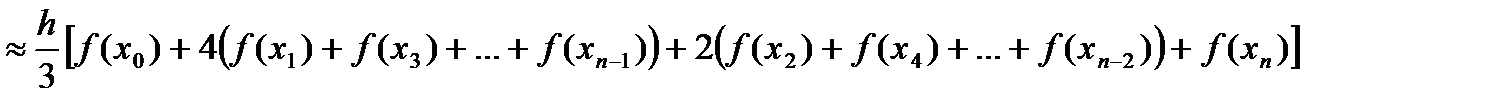(11)
Предлагаем для запоминания следующий вид формулы:
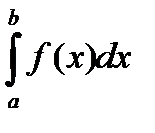
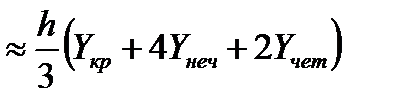(11’)
где Yкр = y 0 + yn,Yнеч = y 1 + y 3 + … + yn- 1 ,Yчет = y 2 + y 4 + … + yn- 2, а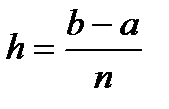 
.
СПИСОК ЛИТЕРАТУРЫ
Основные источники:
1. Григорьев В.П. Элементы высшей математики: учебник для ссузов. – 3-е изд., стер. – М.: Академия, 2007. – 320 с.
2. Высшая математика для экономистов: учебник для вузов/ под ред. Н.Ш. Кремера. – 3-е изд. – М.: ЮНИТИ - ДАНА, 2007. – 479 с.
Дополнительные источники:
1. Богомолов Н.В., Самойленко П.И. Математика. – М.: Дрофа, 2010. – 400 С.
2. Богомолов Н. В. Практические занятия по математике: Учебное пособие для средних профессиональных учебных заведений. Изд. 10-е, перераб. - М.: Высшая школа, 2012. - 495 с.
3. Дадаян А. А. Математика: Учебник для СПО / А. А. Дадаян. - М.: Форум, 2012 - 544 с.
4. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1.: учеб. пос. для вузов. – 7-е изд., испр. – М.: Оникс: Мир и образование, 2008. – 368 с.
5. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2.: учеб. пос. для вузов. – 7-е изд., испр. – М.: Оникс: Мир и образование, 2008. – 448 с.
6. Мордкович А.Г. Алгебра и начала анализа 10-11 кл: учебник. – М.: Мнемозина, 2013. – 224 с.
7. Пехлецкий И. Д. Математика: Учебник для СПО / Пехлецкий И. Д. - 6-е изд., стер. - М.: Академия, 2011 - 304 с.
8. Шипачев В.С. Высшая математика: учебник для вузов. – 8-е изд., стер. – М.: Высшая школа, 2007. – 479 с. (Гриф)
9. Шипачев В.С. Курс высшей математики: учебник. – 2-е изд., перераб. и доп. – М.: ТК Велби, Проспект, 2004. – 600 с.
Интернет-ресурсы:
1. http://www.riis.ru/PS/inet-class.html – Internet-класс по высшей математике: Вся математика, от пределов и производных до методов оптимизации, уравнений математической физики и проверки статистических гипотез в среде самых популярных математических пакетов
2. http://www.exponenta.ru/educat/class/class.asp – Образовательный математический сайт «Экспонента»
3. http://matembook.chat.ru/ – Математика, высшая математика, алгебра, геометрия, дискретная математика
4. http://www.homebook.narod.ru/index.html – Литература по математике (алгебра, геометрия, математический анализ, дискретная математика, дифференциальные уравнения)
5. http://www.history.ru/progmath.htm - Обучающие программы по математике
6. http://www.youtube.com/watch?v=TxFmRLiSpKo (Геометрический смысл производной)
7. http://www.youtube.com/watch?v=PbbyP8oEv-g (Лекция 1. Первообразная и неопределенный интеграл)
8. http://www.youtube.com/watch?v=2N-1jQ_T798&feature=channel (Лекция 5. Интегрирование по частям)
9. http://www.youtube.com/watch?v=3qGZQW36M8k&feature=channel (Лекция 2. Таблица основных интегралов)
10. http://www.youtube.com/watch?v=7lezxG4ATcA&feature=channel (Лекция 3. Непосредственное интегрирование)
11. http://www.youtube.com/watch?v=s-FDv3K1KHU&feature=channel (Лекция 4. Метод подстановки)
12. http://www.youtube.com/watch?v=dU_FMq_lss0&feature=channel (Лекция 12. Понятие определенного интеграла)
