Постановка задачи регрессионного анализа

Лабораторная работа №5. Проведение классического регрессионного анализа

 

Постановка задачи регрессионного анализа

Процедура проведения регрессионного анализа заключается в определении математической модели в форме уравнения (функция регрессии) 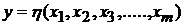, устанавливающего функциональную связь между зависимой переменной 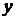и группой независимых переменных 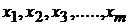с учетом ошибки модели 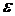. Применение регрессионного анализа оправдано при наличии выборки данных, из которой можно выделить зависимую и ряд независимых переменных. Полученная подобным образом модель позволяет оценивать и прогнозировать изменение зависимой переменной от группы независимых в различных состояниях. Целесообразно применять регрессионный анализ в следующих ситуациях:

- Необходимость моделирования наблюдаемых явлений с целью их более детального изучения, на основании которого формировать управляющие решения. Первостепенная задача в данной ситуации заключается в оценке изменений в одной и более переменных приводящих к изменению в другой переменной, позволяющая установить наличие возможной причинной связи. Например, необходимо выявить основополагающие характеристики формирования курса валют.

- Необходимость моделирования наблюдаемых явлений с целью прогнозирования последующих состояний исследуемой системы. Например, с учетом прогноза экономического состояния страны и внешней политики определить уровень занятости населения.

Используя регрессионный анализ, исследователь сталкивается с рядом проблем:

- адекватная оценка неизвестных параметров регрессионной модели;

-дальнейшая проверка гипотез, выстроенных относительно каждого параметра;

- оценка адекватности итоговой регрессионной модели.

Регрессионный анализ основывается на методе наименьших квадратов. Однако, МНК только подбирает наиболее адекватный вид модели (виды модели для анализа определяет исследователь), а регрессионный анализ расширяет процесс качественной оценки модели (например, оценка связи переменных или упрощение модели), который будет описан ниже.

Формирование задачи на проведение регрессионного анализа начинается с получения выборки наблюдений, отражающих статистические данные, представленные, например, в табличном виде (табл. 1).

Табл. 1. Таблица статистических данных

				……
…….
				…

 

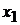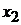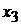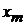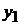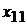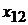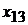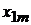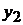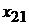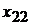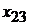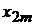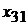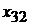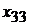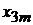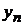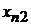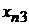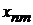В табл. 1 представлены следующие значения:

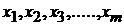- - независимые переменные (факторы, оказывающие влияние на зависимую переменную .

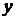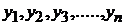- - значения зависимой переменной (отклик) для каждого отдельного наблюдения;

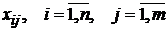- - значение фактора 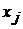при наблюдении 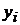(j -я реализация численного значения i -го фактора);

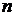- - номер наблюдения.

Важно понимать, что число опытов n, отражающих значение 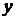в различных вариациях 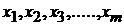, представленных в выборке (табл. 1) должно быть больше числа оцениваемых параметров m (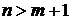). В противном случае при недостаточном числе наблюдений доверять построенной регрессионной модели нельзя.

Таким образом, имеется выборка наблюдений за поведением 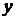в зависимости от изменения 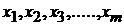. Необходимо определить вид математической модели, описывающей данную зависимость .

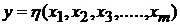Следует также учитывать, что для одного и того же объекта или процесса можно построить несколько моделей, каждая из которых описывает только один интересующий исследователя показатель при измерении одних и тех же независимых переменных. При этом структура моделей будет различна.

 

Уравнение регрессии

Измеряемая выходная характеристика представляет собой следующее соотношение 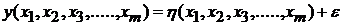(1)

(1)

где

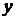- зависимая переменная, описывающая наблюдаемый процесс;

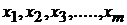- независимые переменные, каждая из которых описывает определенный факт, оказывающий влияние на зависимую переменную.

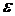- случайная ошибка.

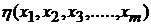- неслучайная величина.

В настоящее время существует множество регрессионных моделей, определяемых видом функции 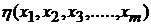, в которой всегда имеются коэффициенты регрессии 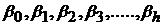, вычисление которых производится на основании экспериментальных данных.

Получим на основании (1) уравнение линейной множественной регрессии по отношению к коэффициентам 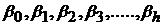в произвольном виде, но не линейную по отношению к факторам 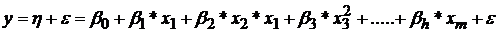(2).

(2)

 

Уравнение множественной регрессии (2) характеризует вид зависимости для каждого отдельно взятого опыта из табл. 1. Так как в данном учебном пособии будут рассматриваться только линейные модели и те нелинейные модели, которые можно посредством преобразований привести к виду линейных по коэффициентам. Запишем уравнение (2) в общем виде (3).

(3)

 

где

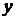- зависимая переменная, описывающая наблюдаемый процесс;

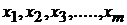- независимые переменные, каждая из которых описывает определенный факт, оказывающий влияние на зависимую переменную.

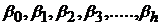- коэффициенты регрессии, вычисляются для каждой 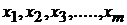и определяют силу и тип взаимосвязи 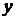по отношению .

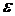- случайная ошибка (невязки, остаточная переменная), указывающая на долю отклонения модели от реального значения наблюдаемого процесса. Случайная ошибка характеризуется факторами (регрессорами) не учтенными в модели по причине слабого влияния на 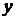и в связи с этим удаленные из модели с целью упрощения, либо не известные факторы, что может быть, например, связано с неверностью представленной выборки.

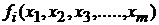- произвольные функции факторов (регрессоры), не включающие неизвестные коэффициенты 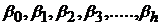. Далее с целью сокращения вместо 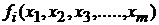будет использовано ;

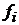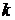- количество регрессоров функции.

 

Коэффициенты регрессии 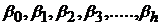играют важную роль при определении взаимосвязи 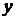по отношению :

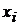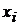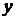1. Если для знак коэффициента положительный, то наблюдается положительная взаимосвязь между и 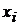(повышение 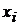приводит к увеличению ).

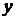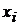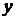2. Если для знак коэффициента отрицательный, то наблюдается отрицательная взаимосвязь между и 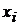(повышение 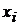приводит к уменьшению ).

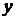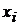3. В том случае, когда имеет достаточно большое значение, то говорят о сильной взаимосвязи и .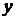

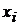4. При значении в пределах близких к 0, говорят о слабой взаимосвязи и .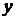

5. 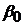- формирует ожидаемое значение 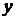в том случае, когда все 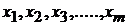равны 0.

Так как результаты наблюдений являются случайными величинами, то применив МНК получить истинные значения коэффициентов 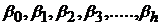из модели (3) невозможно. Поступают следующим образом, на основании данных табл. 1 можно получить их оценки . Так как регрессионная модель определяет зависимость среднего отклика рассчитанного для каждого набора факторов 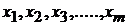без учета случайной ошибки 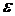введем обозначение рассчитанного отклика, как 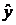(4). Следовательно, далее под 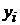будет пониматься отдельно наблюдаемый отклик изучаемого процесса (табл. 1), а под 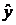предсказанное значение отклика, служащее оценкой истинного значения .

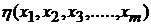(4)