Определение произведения целых неотрицательных чисел через сумму. Законы умножения целых неотрицательных чисел

Теоретико – множественное определение суммы двух целых неотрицательных чисел. Теорема о существовании и единственности суммы с доказательством. Законы сложения целых неотрицательных чисел.

Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Если a = n(A), b = n(B) и A Ç, тоÆB = суммой целых неотрицательных чисел а и b называется число элементов в объединении множеств А и В, т.е. a + b = n(A) + n(B) = n(A È B). Действие, при помощи которого находят сумму, называют сложением, а числа, которые складывают, называют слагаемыми. Сложение обладает коммутативностью и ассоциативностью (переместительный и сочетательный законы). Покажем коммутативность. Для любых множеств А и В выполняется равенство А È В = В È А. Т.к. a = n(A), b = n(B) и A Ç ÆB =, то а + b = n(A) + n(B) = n(А È В) = n(В È А) = n(B) + n(A) = a + b. Аналогично можно показать ассоциативность сложения, которая вытекает из равенства (A È B) È C = A È (B È C). Действительно, a=n(A), b = n(B),c = n(C) и A Ç, BÆB= Ç,ÆC = A Ç, то (a + b) + c = n((AÆC = È B) È C) = n(A È (B È C)) = a + (b + c). Теорема Произведение любых двух целых неотрицательных чисел существует и оно единственное. а,bЄ Zо,۷а*b. (перевернутая А۷ Докажем используя определение №1 1) в>1, а*в = а + а + а…+а (в слагаемое), т.к. сумма существует и единственная => существует и единственное произведение 2) в=1, а*в = а, произведение существует и единственное

3) в=0, а*в = 0,произведение существует и единственное сложение обладает свойствами ассоциативности ((a + b) + c = a + (b + c)) и коммутативности (a + b = b + a). Доказать, что для любых чисел a и b выполняется равенство (a + b) + c = a + (b + c).

Доказательство. Пусть натуральные числа а и b выбраны произвольно, а с принимает различные натуральные значения. Обозначим через М множество всех тех чисел с, для которых равенство (a + b) + c = a + (b + c). Докажем сначала, что 1 содержится в М, т.е. убедимся в справедливости равенства (а + b) + 1 = a + (b + 1).Действительно, по определению сложения (a + b) + c = (a + b) 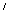= a + b 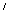= a + (b + 1).Докажем теперь, что если с М, то и с 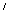М, т.е. из равенства (a + b) + c = a + (b + c) следует равенство (a + b) + c 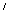= a + (b + c 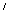). Действительно, по определению сложения, имеем: (a + b) + c 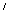=((a + b) + c) 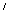= (a + (b + c)) 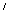= a + (b + c) 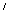= a + (b + c ).

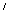Таким образом, мы показали, что множество М содержит 1, и из того, что с содержится в М, следует, что и с 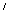М.Следовательно, согласно аксиоме Пеано 4, М = N, т.е. равенство (a + b) + c = a + (b + c) истинно для любого натурального числас. А поскольку числа а и b выбирались произвольно, то истинно и для любых натуральных чисел а и b, что и требовалось доказать.

 

 

Теоретико – множественное определение разности двух целых неотрицательных чисел. Определение разности двух целых неотрицательных чисел через сумму. Теорема о равносильности этих определений с доказательством.

Разностью двух целых неотрицательных чисел а и в называется число элементов дополнения множества В до множества А, таких что n(A)=a, а численность множества n(В)=b и В является подмножеством А.Используя данное определение, мы можем найти нам разность целых неотрицательных чисел. Найдем разность чисел 5 и 2. возьмем два множества таких что n(A)=5, а n(В)=2, В должно быть подмножеством А. А=(a, b, c, d,e) B=(a, b). Найдем дополнение множества В до множества А оно равно B’a =(c, d,e). подсчитаем число элементов дополнения. Мы видим, что оно равно 3 n(В’a)=3=>5-2=3 Действие, при помощи которого находят разность, называется вычитание. Действия вычитания и сложения взаимосвязаны. Эта взаимосвязь находит свое отражение в определении разности через сумму. Разность 2 целых неотриц чисел АиВ - то такое целое неотриц число С, которое при сложении с В дается А. а+в=сó с+в=а

В множестве целых неотрицательных чисел мы не всегда можем найти разность. Условием существования разности заключаются в следующем: разность двух целых неотрицательных чисел существует тогда и только тогда, когда а ≥в Суммой двух целых неотрицательных чисел а и b называется число элементов объединения двух непересекающихся множеств А и В, таких что численность множества n(A)=a, а численность множества n(В)=b/ Используя данное определение мы можем найти сумму любых двух целых неотрицательных чисел. Например, найдем сумму чисел 2 и 3 Возьмем 2 непересекающихся множества А и В, таких что n(A)=2; n(В)=3 и АиВ не пересекаются. А=(n, k) B=(p, s,m) Найдем объединение множеств А и В: А U В=(n, k, p, s,m) посчитаем число элементов этого объединения оно =5 n(A U B)=5 =>2+3=5

 

Два теоретико – множественных определения произведения целых неотрицательных чисел. Теорема о существовании и единственности произведения целых неотрицательных чисел с доказательством.

Если а и в – целые неотрицательные числа (а,bЄ Zо), то произведением а*b называется число, удовлетворяющее следующим условиям:

1.а*b=а+а+…+а; если b >1 и в число слагаемых (это сумма b слагаемых, каждое из которых равно а, при условии, что b>1)

2.аb=а*1=а, если в=1 3.аb=а*0=0, если в=0 Определение 2 Произведением двух целых неотрицательных чисел а и в называется число элементов декартова произведения множеств а и в, таких, что во множестве А-а элементов, во множестве B-b элементов.

Теорема 1. (необходимое условие существования частного). Для того чтобы существовало частное двух натуральных чисел а и b, необходимо, чтобы b ≤.а Доказательство. Пусть частное натуральных чисел а и b существует, т. е. существует такое натуральное число с, что а = с • b. Для любого натурального числа с справедливо утверждение 1 ≤ с. Умножим обе части этого неравенства на натуральное число b, получим b ≤ с • b. Поскольку с • b = а, то b ≤.а Теорема доказана. Теорема 2. (о единственности частного).

Если частное натуральных чисел а и b существует, то оно единственно. Доказательство этой теоремы аналогично доказательству теоремы о единственности разности.

 

 

Определение произведения целых неотрицательных чисел через сумму. Законы умножения целых неотрицательных чисел.

Произведением целых неотрицательных чисел а и в называется целое неотриц.число а*в, удовлетворяющее условиям: 1) а*в=⏟(а+а+⋯+а)┬(в слагаемых) при в>1; 2)а*1=а, при в=1; 3)а*0=0, при в=0. П: по определению 5 имеем: 4*6=4+4+4+4+4+4=24. Действие нахождения произведения называется умножением, а числа а и в называются множителями. Произведение целых неотриц.чисел а и в есть число элементов декартова произведения мн.А и В, где а=п(А), в=п(В), т.е.а*в=п(АхВ), где а=п(А), в=п(В). Во мн.целых неотриц.чисел N0 операция умножения обладает св-ми коммутативности, ассоциативности и дистрибутивности. Коммутативность: (∀а, в ∈N0) а*в=в*а. Док-во: пусть а=п(А) и в=п(В). По определению произведения а*в=п(АхВ). Мн.АхВ и ВхА не равны,т.к.не равны пары чисел (а;в) и (в;а), но АхВ и ВхА яв-ся равномощными. Тогда а*в=п(АхВ)= п(ВхА)= в*а. Значит, а*в=в*а. Ассоциативность: (∀а,в,с∈N0) (а*в)*с= а*(в*с). Док-во: пусть а=п(А), в=п(В), с=п(С). По определению произведения (а*в)*с= п((АхВ)хС), а*(в*с)= п(Ах(ВхС)). Мн.(АхВ)хС и Ах(ВхС) не равны, но яв-ся равномощными. Потому п((АхВ)хС)= п(Ах(ВхС)). Следовательно, (а*в)*с=а*(в*с). Дистрибутивность: (∀а,в,с∈N0) (а+в)*с= а*с+в*с. Док-во: пусть а=п(А), в =п(В), с=п(С). По определению произведения (а+в)*с= п((А∪В)хС); а*с+в*с= п((АхС)∪(ВхС)). На основании св-ва дистрибутивности декартова произведения мн.имеем: (А∪В)хС= (АхС)∪(ВхС). Из этого вытекает, что мощность мн.(А∪В)хС и (АхС)∪(ВхС) тоже равны, т.е.п((А∪В)хС)= п((АхС)∪(ВхС)). Следовательно, (а+в)*с= а*с+в*с. П: 97*5=(90+7)*5=90*5+7*5=450+35=485. Законы: 1.переместительный: для любых целых неотриц.чисел а и в справедливо равенство а*в=в*а. 2.сочетательный: для любых целых неотриц.чисел а, в,с справедливо равенство (а*в)*с= а*(в*с). 3.распределительный закон умножения относительно сложения: для дюбых целых неотриц.чисел а,в,с справедливо равенство (а+в)*с= ас+вс. 4.распределительный закон умножения относительно вычитания: для любых целых неотриц.чисел а,в и с и а≥в справедливо равенство (а-в)с=ас-вс.

 

 

Теоретико – множественное истолкование деления во множестве натуральных чисел. Определение частного через произведение. Теорема о равносильности двух определений частного с доказательством.

Деление целого неотрицательного числа на натуральное число связа- но с разбиением множества на классы. Если а – число элементов множества А и множество А разбито на b попарно непересекающихся подмножеств, то частным чисел а и b назы- вается число элементов каждого подмножества разбиения. Если а – число элементов множества А и множество А разбито на по- парно непересекающиеся подмножества, в каждом из которых b элемен- тов, то частным чисел а и b называется число подмножеств разбиения. Действие, при помощи которого находят частное, называется делени- ем, число а – делимым, число b – делителем. Познакомимся с некоторыми свойствами деления натуральных чи- сел. Правило деления суммы на число. Если числа а и b делятся на чис- ло с, то и их сумма а + b делится на с. Частное, получаемое при делении суммы а + b на число с, равно сумме частных получаемых при делении а на с и b на с, т.е. (а + b): с = а: с + b: с. Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(c) и полученное частное разделить на с(b): а: (b × c) = (a: b): c = (a: c): b. Правило умножения числа на частное двух чисел. Чтобы умно- жить число на частное двух чисел, достаточно умножить это число на де- лимое и полученное произведение разделить на делитель, т.е. a × (b: c) = = (a × b): c. Правило деления произведения на число. Чтобы разделить произве- дение нескольких целых неотрицательных чисел на натуральное число, достаточно один из множителей разделить на это число и полученное ча- 16 стное умножить на оставшиеся множители, т.е., если а: n, то (a × b × c): n = = (a: n) × b × c. Задача 27. Дадим теоретико-множественное обоснование равенству 6: 3 = 2. Решение. Возьмем множество А, в котором 6 элементов, например А = {a, b, c, d, e, f}. Разобьем множество А на 3 попарно непересекающихся равномощных множества, например А 1={a, b}, А 2 = {c, d}, А 3 = {e, f}. В каждом подмножестве по 2 элемента: n(А 1) = n(А 2) = n(А 3) = 2. Следовательно, 6: 3 = 2. Справедливость данного равенства можно объяснить и так. Возьмем данное нам множество А и разобьем его на подмножества, в каждом из ко- торых по 3 элемента, например: А 1 = {a, b, с}, А 2 = {d, e, f}. Таких подмно- жеств в разбиении будет два. Следовательно, 6: 3 = 2. Опр.Частным целого неотрицательного числа а и натурального числа b называется тоже целое неотрицательное число с, что а: b=с<=>b*c=a (<=> - тогда и только тогда, когда)Теорема: Для того, чтобы частное а и b существовало, необходимо чтобы b не превосходило а. (а ≥ b)