Задание к типовому расчету
1. Составить вариационный ряд.
2. Составить сгруппированный статистический ряд.
3. Построить гистограмму выборки.
4. Построить график эмпирической функции распределения.
5. Найти выборочное среднее, выборочное среднеквадратическое отклонение, коэффициенты асимметрии и эксцесса.
6. Построить доверительный интервал для математического ожидания при доверительной вероятности 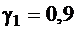 .
.
7. Построить доверительный интервал для среднеквадратического отклонения при доверительной вероятности 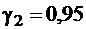 .
.
8. Проверить с помощью критерия Пирсона гипотезу 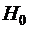 о том, что генеральная совокупность распределена по нормальному закону.
о том, что генеральная совокупность распределена по нормальному закону.
Примервыполнения статистическогорасчета
Пусть в результате некоторого эксперимента получено n значений изучаемой случайной величины Х. Данные записаны в виде таблицы и составляют первичную выборкуобъема n =100.
| 81,38 | 66,94 | 88,26 | 72,73 | 65,72 | 109,76 | 88,45 | 96,73 | 85,90 | 66,93 |
| 61,31 | 86,73 | 89,03 | 65,14 | 80,06 | 93,68 | 69,09 | 57,56 | 74,79 | 77,66 |
| 83,88 | 54,58 | 58,83 | 78,05 | 67,33 | 70,51 | 60,18 | 67,01 | 52,27 | 50,84 |
| 63,83 | 72,92 | 69,22 | 71,12 | 88,77 | 45,84 | 98,34 | 76,98 | 57,34 | 79,80 |
| 63,29 | 66,80 | 78,64 | 74,30 | 56,75 | 77,85 | 71,95 | 67,63 | 69,32 | 58,53 |
| 58,55 | 39,92 | 73,16 | 96,09 | 70,44 | 67,22 | 73,04 | 59,72 | 72,19 | 65,53 |
| 86,60 | 65,12 | 74,32 | 77,27 | 79,60 | 79,95 | 61,63 | 45,51 | 104,02 | 84,87 |
| 71,36 | 68,05 | 51,88 | 81,18 | 75,06 | 85,37 | 50,82 | 87,18 | 64,12 | 86,93 |
| 71,90 | 30,03 | 49,98 | 42,52 | 60,96 | 99,11 | 78,32 | 44,69 | 43,08 | 79,58 |
| 60,85 | 64,43 | 95,54 | 89,67 | 57,37 | 98,60 | 80,13 | 67,04 | 77,00 | 69,26 |
1. Представим выборку в виде вариационного ряда: последовательностиисходных величин, записанных в возрастающем порядке.
| 30,03 | 61,63 | 71,36 | 80,13 |
| 39,92 | 63,29 | 71,90 | 81,18 |
| 42,52 | 63,83 | 71,95 | 81,38 |
| 43,08 | 64,12 | 72,19 | 83,88 |
| 44,69 | 64,43 | 72,73 | 84,87 |
| 45,51 | 65,12 | 72,92 | 85,37 |
| 45,84 | 65,14 | 73,04 | 85,90 |
| 49,98 | 65,53 | 73,16 | 86,60 |
| 50,82 | 65,72 | 74,30 | 86,73 |
| 50,84 | 66,80 | 74,32 | 86,93 |
| 51,88 | 66,93 | 74,79 | 87,18 |
| 52,27 | 66,94 | 75,06 | 88,26 |
| 54,58 | 67,01 | 76,98 | 88,45 |
| 56,75 | 67,04 | 77,00 | 88,77 |
| 57,34 | 67,22 | 77,27 | 89,03 |
| 57,37 | 67,33 | 77,66 | 89,67 |
| 57,56 | 67,63 | 77,85 | 93,68 |
| 58,53 | 68,05 | 78,05 | 95,54 |
| 58,55 | 69,09 | 78,32 | 96,09 |
| 58,83 | 69,22 | 78,64 | 96,73 |
| 59,72 | 69,26 | 79,58 | 98,34 |
| 60,18 | 69,32 | 79,60 | 98,60 |
| 60,85 | 70,44 | 79,80 | 99,11 |
| 60,96 | 70,51 | 79,95 | 104,02 |
| 61,31 | 71,12 | 80,06 | 109,76 |
2. Составим группированный статистический ряд. Найдем наименьший и наибольший элемент выборки: 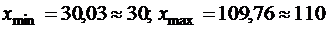 . Разобьем отрезок
. Разобьем отрезок 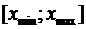 на
на 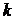 равных по длине промежутков.При объеме выборки n= 100 рекомендуется взять
равных по длине промежутков.При объеме выборки n= 100 рекомендуется взять  Число
Число 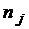 – частота попадания элементов выборки в
– частота попадания элементов выборки в 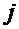 -ый промежуток.
-ый промежуток.
Таблица 1
| Интервал | [30; 40] | (40; 50] | (50; 60] | (60; 70] | (70; 80] | (80; 90] | (90; 100] | (100; 110] |
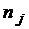
|
3. Для построения гистограммы дополним таблицу 1тремя строками: 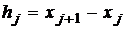 ,
, 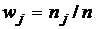 и
и 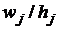 , где
, где 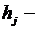 длина
длина 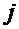 - ого промежутка;
- ого промежутка; 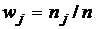 – относительная частота попадания элементов выборки в
– относительная частота попадания элементов выборки в 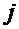 -ый промежуток.
-ый промежуток.
Таблица 2
| Интервал | [30; 40] | (40; 50] | (50; 60] | (60; 70] | (70; 80] | (80; 90] | (90; 100] | (100; 110] |
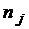
| ||||||||

| ||||||||
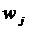
| 0,02 | 0,06 | 0,14 | 0,26 | 0,28 | 0,15 | 0,07 | 0,02 |
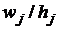
| 0,002 | 0,006 | 0,014 | 0,026 | 0,028 | 0,015 | 0,007 | 0,002 |
Последняя строка таблицы2 определяет высоты столбцов гистограммы, приведенной на рисунке 1.
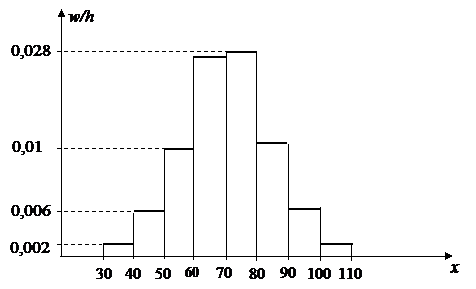
Рис. 1
Для непрерывной случайной величины гистограмма аппроксимирует плотность вероятности генеральной совокупности.
4. Для построения графика эмпирической функции распределения в таблицу 1 добавим две строки, в которых следует записать значения 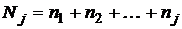 и
и 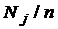 .
.
Таблица 3
| Интервал | [30; 40] | (40; 50] | (50; 60] | (60; 70] | (70; 80] | (80; 90] | (90; 100] | (100; 110] |
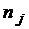
| ||||||||
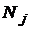
| ||||||||
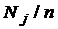
| 0,02 | 0,08 | 0,22 | 0,48 | 0,76 | 0,92 | 0,98 |
Значения эмпирической функции распределения равны 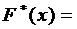
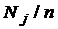 , если
, если 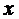 принадлежит
принадлежит 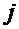 - ому промежутку;
- ому промежутку; 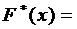 0, если
0, если 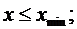 и
и 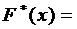 1, если
1, если 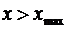 . Получим
. Получим

График эмпирической функции распределения (кумулята) имеет вид:
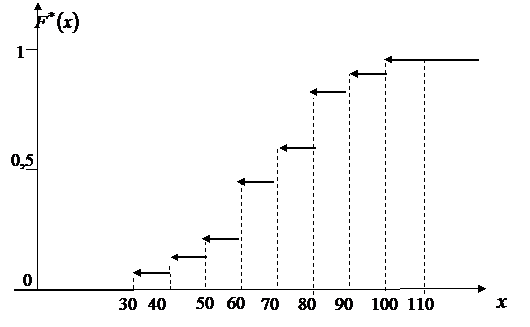
Рис. 2
Эмпирическая функция 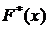 аппроксимирует функцию распределения генеральной совокупности.
аппроксимирует функцию распределения генеральной совокупности.
5. Для вычисления числовых характеристик выборки построимновый вариационный ряд.Обозначим 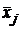 – середину
– середину 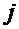 - того промежутка. Этозначение присваивается всем элементам выборки, попавшим в
- того промежутка. Этозначение присваивается всем элементам выборки, попавшим в 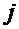 -ый интервал.
-ый интервал.
Таблица 4
| Интервал | 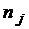
| 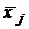
| 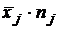
| 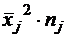
|
| [30; 40] | ||||
| (40; 50] | ||||
| (50; 60] | ||||
| (60; 70] | ||||
| (70; 80] | ||||
| (80; 90] | ||||
| (90; 100] | ||||
| (100; 110] | ||||
| Сумма |
Для группированного ряда выборочное среднее 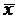 и выборочная дисперсия
и выборочная дисперсия 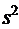 вычисляются по формулам:
вычисляются по формулам:
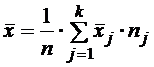 ;
;
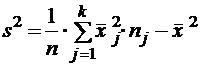 ;
;
Подставляя величины, приведенные в таблице 4, получим:
 ;
;
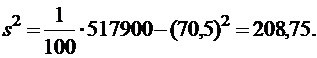
Выборочное среднеквадратическое отклонение 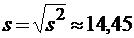 .
.
Замечание. При расчетах результат округляем до двух десятичных знаков.
Составим ещё одну таблицу.
Таблица 5
| Интервал | 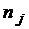
| 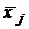
| 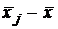
| 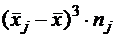
| 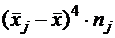
|
| [30; 40] | -35,5 | -89477,75 | 3176460,13 | ||
| (40; 50] | -25,5 | -99488,25 | 2536950,38 | ||
| (50; 60] | -15,5 | -52134,25 | 808080,88 | ||
| (60; 70] | -5,5 | -4325,75 | 23791,63 | ||
| (70; 80] | 4,5 | 2551,50 | 11481,75 | ||
| (80; 90] | 14,5 | 45729,38 | 663075,94 | ||
| (90; 100] | 24,5 | 102942,88 | 2522100,44 | ||
| (100; 110] | 34,5 | 82127,25 | 2833390,13 | ||
| Сумма | –12075 | 12575331,25 |
Коэффициенты асимметрии А и эксцесса Е вычисляются по формулам:
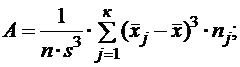
 .
.
Подставляя величины, приведенные в таблице 4, получим:
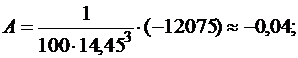
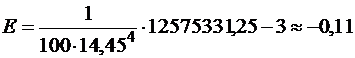 .
.
Если коэффициенты А и Е значительно отклоняются от нулевого значения, то выборочное распределение отличается от нормального.
Замечание. При n < 30 в расчетах следует использовать исправленную оценку среднеквадратического отклонения 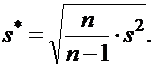
6. Оценку истинного значения параметра а (математического ожидания)дает доверительный интервал, который для случая большой выборки определяется формулой
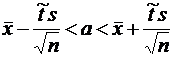 ,
,
где значение 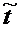 находится из условия
находится из условия 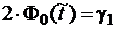 .
.
Для доверительной вероятности (надежности) 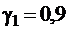 по таблице значений функции Лапласа
по таблице значений функции Лапласа 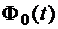 , приведенной в приложении 2, находим число 0,4505, наиболее близкое к
, приведенной в приложении 2, находим число 0,4505, наиболее близкое к 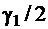 . Это число расположено в строке, именованной «1,6», и столбце с названием «5». Искомое значение
. Это число расположено в строке, именованной «1,6», и столбце с названием «5». Искомое значение 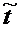 = 1,6 + 0,05 = 1,65, так как
= 1,6 + 0,05 = 1,65, так как 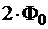 (1,65)» 0,9.При
(1,65)» 0,9.При 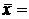 70,5 и точности оценки
70,5 и точности оценки  2,61с надежностью 0,9 доверительный интервал для математического ожидания равен(68,12; 72,88).
2,61с надежностью 0,9 доверительный интервал для математического ожидания равен(68,12; 72,88).
7. Оценку истинного значения параметра 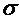 дает доверительный интервал для среднеквадратического отклонения, который для случая большой выборки определяется по формуле
дает доверительный интервал для среднеквадратического отклонения, который для случая большой выборки определяется по формуле
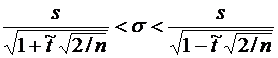 .
.
По заданной доверительной вероятности 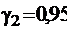 по таблице значений функции Лапласа, находим
по таблице значений функции Лапласа, находим 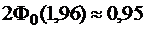 , следовательно,
, следовательно, 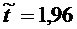 . Тогда с надежностью 0,95доверительный интервал для среднеквадратического отклонения
. Тогда с надежностью 0,95доверительный интервал для среднеквадратического отклонения 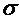 имеет вид (12,78; 16,99).
имеет вид (12,78; 16,99).
8. Проверка нулевой гипотезы 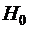 по критерию Пирсона состоит из следующих этапов.
по критерию Пирсона состоит из следующих этапов.
a) По выборке вычисляются точечные оценки математического ожидания 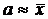 и среднеквадратического отклонения
и среднеквадратического отклонения 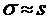 .
.
b) В каждом промежутке определяются эмпирические частоты и теоретические вероятности.
c) Для данной выборки вычисляется наблюдаемое значение  критерия Пирсона.
критерия Пирсона.
d) Задается уровень значимости 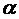 и подсчитывается количество степеней свободы.
и подсчитывается количество степеней свободы.
e) По таблице приложения 3 определяется значение 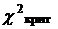 .
.
f) Если 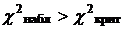 , то гипотеза
, то гипотеза 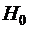 отвергаетсякак маловероятная.
отвергаетсякак маловероятная.
Значения коэффициентов асимметрии А и эксцесса Е, близкие к нулю, а также вид гистограммыпозволяют выдвинуть гипотезу 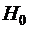 о том, что генеральная совокупность распределена по нормальному закону.Проверим эту гипотезу с помощью критерия Пирсона.
о том, что генеральная совокупность распределена по нормальному закону.Проверим эту гипотезу с помощью критерия Пирсона.
а) Этот этап проделан в пункте 5.
b) Используя таблицу приложения 2, найдем теоретические вероятности попадания варианты в каждый промежуток по формуле
 ,
,
и вычислим 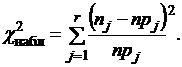
Вычисления удобно проводить по таблице 6. Предварительно следует изменить таблицу 1, объединив первый интервал со вторым и седьмой интервал с восьмым, так как в критерии Пирсона предполагается, что количество вариант в каждом интервале не меньше пяти. Крайние интервалы расширяются влево и вправо до бесконечности, причем 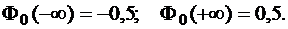
Таблица 6
| Интервал | (– ¥; 50] | (50;60] | (60; 70] | (70; 80] | (80; 90] | (90; ¥) | |||||||
Граница 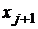
| |||||||||||||
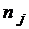
| |||||||||||||
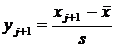
| – 1,42 | – 0,73 | – 0,03 | 0,66 | 1,35 | ||||||||
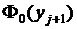
| – 0,5 | – 0,42 | – 0,27 | – 0,01 | 0,25 | 0,41 | 0,5 | ||||||
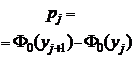
| 0,08 | 0,15 | 0,26 | 0,26 | 0,17 | 0,09 | |||||||

| |||||||||||||
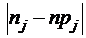
| |||||||||||||
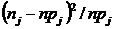
| 0,07 | 0,15 | 0,24 |
Сначала в граничных точках вычисляем аргументы функции Лапласа. Например, для промежутка (70; 80]имеем
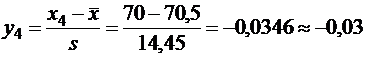 ,
,
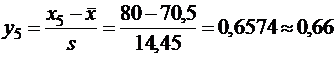 .
.
По таблице приложения 2 вычисляем теоретическую вероятность  попадания варианты в промежуток(70; 80]
попадания варианты в промежуток(70; 80]
 .
.
Функция 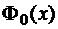 является нечетной, следовательно,
является нечетной, следовательно,
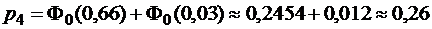 .
.
В последней строке таблицы 6 помещены значения 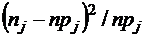 .Для промежутка[70; 80) эта величина принимает значение
.Для промежутка[70; 80) эта величина принимает значение
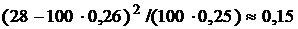 .
.
c)Суммируя все числа последней строки, получаем 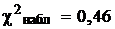 . Полученное число необходимо сравнить с величиной
. Полученное число необходимо сравнить с величиной 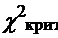 .
.
d) Количество интервалов 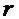 вариационного ряда, приведенного в таблице 6, равно шести.Число степеней свободы
вариационного ряда, приведенного в таблице 6, равно шести.Число степеней свободы 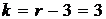 .
.
e) Выбираем уровень значимости  . В таблице приложения 3 параметрам
. В таблице приложения 3 параметрам 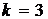 и
и 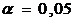 соответствует значение
соответствует значение 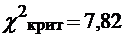 .
.
f) Привыбранной надежности 0,95 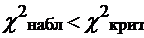 . Следовательно, отвергать гипотезу
. Следовательно, отвергать гипотезу 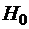 оснований нет. Предположение о том, что исследуемая физическая величина распределена по нормальному закону с параметрами
оснований нет. Предположение о том, что исследуемая физическая величина распределена по нормальному закону с параметрами 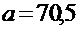 ;
; 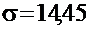 не противоречит результатам измерений.
не противоречит результатам измерений.
Значит, можно считать, что функция плотности вероятности изучаемой физической величины имеет вид.
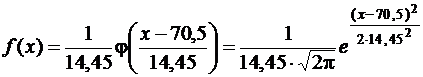 .
.
Значения функции  приведены в таблице приложения 1, аграфик
приведены в таблице приложения 1, аграфик 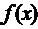 изображен на рисунке 3 сплошной линией. Отдельные точки на том же рисунке последней строке таблицы 1, по которой строилась гистограмма. Очевидно, что теоретическое распределение вполне согласуется с результатами выборки.
изображен на рисунке 3 сплошной линией. Отдельные точки на том же рисунке последней строке таблицы 1, по которой строилась гистограмма. Очевидно, что теоретическое распределение вполне согласуется с результатами выборки.
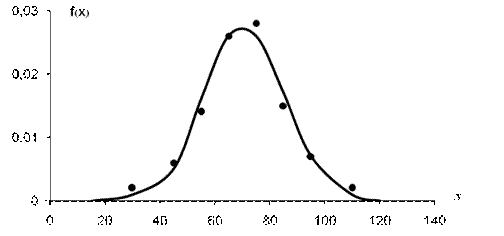
Рис. 3
ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Вариант 1 Вариант 2 Вариант 3
| 0,92 | -2,06 | -0,07 | 1,70 | 0,81 | 0,08 | 0,09 | 3,03 | 1,16 | ||
| 0,47 | 2,91 | -0,51 | 1,08 | 4,02 | 1,78 | -0,22 | 1,33 | -1,63 | ||
| -1,41 | 0,85 | -2,26 | 1,17 | 2,82 | -1,01 | -0,79 | 0,49 | -1,06 | ||
| -0,30 | -0,54 | -0,64 | 1,56 | 3,12 | -0,67 | -0,53 | -0,50 | 2,35 | ||
| 0,85 | -0,17 | -1,02 | 1,60 | 2,37 | 2,11 | 2,18 | -0,14 | 5,37 | ||
| -0,74 | 3,51 | 2,39 | -1,28 | 1,44 | -1,60 | 0,83 | 3,26 | 3,59 | ||
| 2,36 | -0,30 | 0,31 | -0,98 | 3,35 | -0,21 | -2,05 | 0,80 | 1,71 | ||
| -0,38 | -1,78 | 2,23 | 0,08 | 1,74 | 0,67 | 2,55 | 4,03 | 2,27 | ||
| -0,48 | -0,68 | 1,30 | 1,79 | -0,50 | 2,31 | 2,02 | 3,24 | 1,01 | ||
| 1,22 | -1,41 | 0,13 | 5,41 | -0,31 | -1,17 | 1,30 | 0,92 | 2,85 | ||
| -0,93 | 0,95 | 2,08 | 1,16 | 2,36 | 2,05 | -0,74 | 2,42 | 6,61 | ||
| 1,73 | 0,00 | 1,56 | 1,17 | 0,52 | -0,23 | 2,07 | 4,65 | 1,80 | ||
| -3,76 | -0,93 | 1,12 | 2,15 | -3,11 | 1,84 | -0,04 | -1,46 | 0,63 | ||
| 3,83 | -1,70 | -1,24 | 1,91 | 2,50 | 5,27 | -2,15 | 5,05 | 1,82 | ||
| -0,13 | 1,15 | -0,40 | 1,71 | -0,33 | -1,33 | -0,96 | 1,85 | 2,45 | ||
| 0,68 | -0,52 | -0,85 | 2,61 | 0,79 | 2,55 | 0,74 | 3,24 | 2,70 | ||
| 1,85 | -1,81 | 0,41 | -1,16 | -1,51 | -2,30 | -2,34 | 0,39 | -0,14 | ||
| -1,39 | -2,25 | 0,81 | 0,21 | 3,67 | 2,63 | 2,19 | 2,01 | 2,96 | ||
| -3,34 | -0,72 | -1,43 | 1,06 | 0,50 | -1,22 | -0,71 | 1,35 | 2,26 | ||
| 1,56 | 0,03 | -0,59 | -0,83 | 1,62 | 1,85 | 0,33 | 3,28 | 2,62 | ||
| 0,31 | -0,66 | 2,53 | -1,43 | -1,25 | 1,03 | -1,64 | 3,05 | 2,33 | ||
| -1,16 | 0,79 | -0,93 | -0,42 | -1,90 | 3,84 | 2,02 | 4,60 | 2,59 | ||
| -0,31 | 1,48 | -0,16 | 3,56 | 0,18 | 0,06 | 2,13 | 2,03 | 5,68 | ||
| -0,07 | -1,54 | 0,83 | 3,68 | 0,08 | 0,30 | -1,09 | 4,22 | 3,78 | ||
| 0,17 | 0,55 | 2,39 | 1,93 | 1,49 | 1,46 | 2,86 | 2,02 | 8,37 | ||
| 0,52 | 0,04 | 1,84 | 3,33 | -0,32 | -0,47 | 3,92 | 2,16 | 2,09 | ||
| -0,10 | 0,41 | -1,36 | -0,02 | 4,23 | 1,51 | 4,23 | 1,64 | 4,26 | ||
| -0,21 | 0,44 | 0,03 | 0,97 | 0,81 | 1,84 | 2,46 | 0,20 | 2,00 | ||
| -0,21 | 0,00 | -0,47 | 1,28 | 0,13 | 2,48 | 4,53 | 2,21 | 2,73 | ||
| 0,88 | 1,87 | 0,03 | 1,40 | 1,89 | 0,01 | 5,27 | 3,78 | 0,69 | ||
| 0,61 | -2,09 | -2,35 | -0,99 | 0,01 | 1,13 | 4,68 | 2,42 | 4,22 | ||
| 2,25 | 1,57 | 2,08 | 2,12 | -1,02 | 0,53 | 1,75 | 4,98 | 6,33 | ||
| -1,40 | 0,07 | 2,09 | 3,33 | -2,74 | 3,79 | 1,21 | 2,95 | 1,78 | ||
| 0,59 | -0,06 | -0,24 | ||||||||
| γ1 = | 0,95 | γ1 = | 0,95 | γ1 = | 0,95 | |||||
| γ2 = | 0,90 | γ2 = | 0,85 | γ2 = | 0,80 |
Вариант 4 Вариант 5 Вариант 6
| 7,43 | 1,41 | 5,91 | 1,67 | 7,50 | 2,98 | 6,58 | 3,56 | -1,41 | ||
| 2,24 | -0,15 | 1,12 | 0,67 | 4,37 | 4,34 | 2,19 | -0,92 | 5,76 | ||
| 4,21 | 3,54 | 1,50 | 3,31 | 3,81 | 6,13 | 8,23 | 5,31 | 4,71 | ||
| 3,51 | 3,85 | 1,21 | 3,00 | 4,24 | 8,19 | 1,99 | 7,65 | 0,03 | ||
| 5,95 | 5,33 | 1,01 | 3,90 | 1,83 | 5,26 | 8,08 | 4,64 | 5,25 | ||
| -0,35 | 3,74 | 1,17 | 9,53 | 3,76 | 9,81 | 3,53 | 7,86 | 6,09 | ||
| -0,20 | 3,02 | 3,13 | 6,57 | 5,35 | 3,39 | 2,80 | 3,91 | 1,74 | ||
| 3,09 | 3,54 | 7,23 | 5,27 | 2,79 | 1,09 | 9,39 | 6,25 | 1,89 | ||
| 3,34 | 3,38 | 3,67 | 7,34 | 0,31 | 8,47 | 3,10 | 5,32 | 0,28 | ||
| 3,25 | 0,59 | 8,95 | 4,02 | 5,13 | 6,01 | 5,50 | 5,12 | 4,43 | ||
| 1,84 | 2,75 | 3,40 | 5,48 | 3,57 | 2,10 | 1,11 | 7,02 | 2,80 | ||
| 5,08 | 4,41 | 5,03 | 0,36 | 1,74 | 1,45 | 0,90 | 5,84 | 3,01 | ||
| 4,68 | 6,40 | 6,67 | 4,26 | 4,06 | 6,33 | 4,76 | 8,29 | 5,65 | ||
| -2,37 | 3,92 | 5,97 | 2,47 | 3,86 | 7,36 | -0,73 | 5,39 | 5,13 | ||
| 2,33 | 0,36 | 4,77 | 2,35 | 3,95 | 1,80 | 0,66 | 8,76 | 0,21 | ||
| 2,73 | 0,63 | 4,16 | 2,39 | 4,07 | 2,44 | 6,75 | 7,18 | 4,43 | ||
| 3,92 | 2,40 | 1,17 | 1,38 | 8,92 | 2,18 | 2,27 | 2,28 | 7,00 | ||
| 4,25 | 2,60 | 0,85 | 3,22 | 5,71 | 0,24 | 4,35 | 4,98 | 5,51 | ||
| 4,14 | -0,31 | 2,71 | 0,73 | -1,63 | 8,26 | 8,22 | 7,52 | 6,03 | ||
| 4,65 | -0,71 | 4,12 | 2,77 | 2,66 | 1,42 | 8,05 | 2,32 | 5,56 | ||
| 5,50 | 3,25 | 6,85 | 1,96 | 3,47 | 3,41 | 1,47 | 1,28 | 4,80 | ||
| 5,21 | 1,48 | 3,25 | 10,07 | 4,99 | 2,94 | 7,41 | 3,66 | 7,71 | ||
| 6,76 | 4,77 | 1,19 | 7,20 | 4,83 | 7,35 | 0,51 | 0,83 | 8,48 | ||
| 3,27 | 6,35 | -1,76 | 3,83 | 2,97 | 6,67 | 2,05 | 3,96 | 2,98 | ||
| 3,56 | -1,49 | 3,69 | 2,45 | 5,77 | 7,76 | 6,52 | 6,35 | 2,38 | ||
| 2,22 | 4,86 | 0,07 | 3,63 | 6,42 | 8,26 | 5,15 | 4,48 | 5,65 | ||
| 0,81 | 1,17 | 2,60 | 2,68 | 3,55 | 3,05 | 3,82 | 1,26 | 5,38 | ||
| 0,47 | 6,82 | 2,73 | 5,80 | 6,99 | 6,11 | 6,95 | 10,97 | 6,75 | ||
| 6,58 | 2,24 | 1,55 | 3,15 | 4,05 | 7,87 | 3,15 | 5,71 | 8,57 | ||
| 3,36 | 2,69 | 2,46 | -0,62 | 5,81 | 7,00 | 8,33 | 6,77 | 8,55 | ||
| 7,05 | 0,50 | 3,87 | 5,08 | 4,07 | 1,23 | 4,07 | 1,35 | -0,55 | ||
| 7,63 | 0,54 | 4,05 | 3,27 | 0,42 | 5,42 | 7,76 | 6,44 | 3,99 | ||
| 0,67 | 4,03 | 1,68 | 3,25 | 2,23 | 4,84 | 5,26 | 5,76 | 6,45 | ||
| -0,24 | 2,94 | 4,59 | ||||||||
| γ1 = | 0,90 | γ1 = | 0,90 | γ1 = | 0,90 | |||||
| γ2 = | 0,95 | γ2 = | 0,85 | γ2 = | 0,80 |
Вариант7 Вариант8 Вариант9
| 5,24 | 8,35 | 3,82 | 8,30 | 9,69 | 5,17 | 3,37 | 10,72 | 7,76 | ||
| 4,19 | 10,86 | 6,45 | 11,34 | 3,03 | 8,13 | 3,50 | 5,84 | 6,75 | ||
| 6,48 | 3,34 | 9,82 | 14,57 | 13,29 | 3,84 | 5,65 | 11,85 | 8,50 | ||
| 7,19 | 4,70 | 9,73 | 4,50 | 12,35 | 6,24 | 7,84 | 2,89 | 4,76 | ||
| 5,21 | 8,55 | 10,30 | 7,25 | 4,54 | 7,09 | 11,54 | 6,60 | 9,87 | ||
| 3,40 | 7,02 | 4,78 | 5,25 | 9,79 | 4,21 | -0,32 | 9,90 | 12,12 | ||
| 8,66 | -2,99 | 2,41 | 3,95 | 11,98 | 5,23 | 3,96 | 10,12 | 8,65 | ||
| 2,86 | 5,72 | 6,37 | 7,45 | 10,25 | 1,64 | 4,91 | 6,17 | 16,25 | ||
| 8,23 | 13,55 | 3,37 | 3,59 | 6,49 | 10,90 | 2,51 | 6,59 | 6,67 | ||
| 9,31 | 2,72 | 6,45 | 7,27 | 4,06 | 5,26 | 5,50 | 3,04 | 6,43 | ||
| 8,09 | 7,33 | 2,75 | 5,94 | 8,61 | 8,97 | 13,26 | 9,98 | 5,99 | ||
| 5,32 | 8,09 | 8,74 | 8,05 | 5,49 | 6,10 | 10,51 | 8,00 | 9,67 | ||
| 7,61 | 8,49 | 9,85 | 6,42 | 9,03 | 6,04 | 6,31 | 6,13 | 7,78 | ||
| 7,19 | 10,21 | 2,66 | 6,24 | 9,70 | 11,85 | 9,41 | 7,00 | 15,13 | ||
| 3,54 | 7,07 | 3,03 | 9,84 | 0,36 | 9,16 | 9,32 | 8,67 | 6,50 | ||
| 6,00 | 4,59 | 0,48 | 7,72 | 9,56 | 7,18 | 14,19 | 11,39 | 6,98 | ||
| 8,09 | 4,67 | 5,86 | 7,30 | 6,83 | 12,31 | 9,36 | 6,47 | 2,20 | ||
| 7,95 | 9,56 | -0,59 | 5,89 | 6,35 | 7,56 | 2,82 | 7,54 | 3,46 | ||
| 4,25 | 6,62 | 2,29 | 1,64 | 2,69 | 9,62 | 1,69 | 8,20 | 13,27 | ||
| 4,61 | 2,15 | 7,81 | 9,12 | 0,34 | 4,24 | 5,91 | 5,55 | 9,15 | ||
| 4,16 | 2,38 | 5,41 | 13,76 | 8,45 | 9,80 | 11,32 | 2,32 | 6,33 | ||
| 6,20 | 4,90 | 7,44 | 6,72 | 6,68 | 3,99 | 5,62 | 2,46 | 4,57 | ||
| 9,45 | 2,52 | 3,91 | 10,47 | 9,98 | 7,88 | 11,56 | 11,46 | 7,01 | ||
| 7,27 | 5,15 | 7,75 | 7,13 | 2,52 | 5,03 | 13,48 | 9,84 | 5,96 | ||
| 10,64 | 9,31 | 7,19 | 1,14 | 9,16 | 5,03 | 8,21 | 9,09 | 5,41 | ||
| 6,11 | 4,42 | 8,21 | 9,33 | 2,58 | 3,62 | 9,20 | 7,68 | 10,45 | ||
| 7,10 | 8,77 | 11,26 | 3,01 | 4,95 | 4,44 | 7,14 | 9,92 | 10,98 | ||
| 3,28 | 3,68 | 5,49 | 4,72 | 7,48 | 8,51 | 12,48 | 8,39 | 10,76 | ||
| 5,52 | 3,12 | 1,59 | 5,22 | 9,18 | 14,26 | 7,90 | 9,18 | 13,78 | ||
| 3,23 | 4,78 | 1,36 | 6,94 | 12,36 | 8,08 | 8,21 | 11,27 | 10,26 | ||
| 8,88 | 5,09 | 10,04 | 7,60 | 6,45 | 4,30 | 14,58 | 6,41 | 7,32 | ||
| 5,63 | 4,02 | 7,05 | 8,55 | 4,40 | 7,65 | 12,31 | 9,71 | 8,67 | ||
| 6,51 | 11,12 | 8,32 | 7,91 | 7,21 | 1,77 | 11,09 | 7,75 | 10,65 | ||
| 8,01 | 10,40 | 6,04 | ||||||||
| γ1 = | 0,85 | γ1 = | 0,85 | γ1 = | 0,85 | |||||
| γ2 = | 0,90 | γ2 = | 0,95 | γ2 = | 0,80 |
Вариант 10 Вариант 11 Вариант 12
| 12,95 | 8,44 | 16,16 | 1,95 | 10,38 | 8,69 | 6,15 | 13,79 | 15,26 | ||
| 4,42 | 11,39 | 10,43 | 13,10 | 12,72 | 8,83 | 9,48 | 7,98 | 7,95 | ||
| 11,82 | 7,94 | 12,55 | 13,39 | 12,23 | 7,42 | 6,00 | 10,30 | 15,37 | ||
| 10,82 | 11,59 | 11,42 | 15,40 | 12,08 | 6,58 | 12,74 | 13,06 | 14,41 | ||
| 12,08 | 13,54 | 14,24 | 9,27 | 10,83 | 10,74 | 13,10 | 6,28 | 10,56 | ||
| 11,98 | 7,91 | 10,13 | 12,57 | 7,48 | 16,17 | 9,74 | 15,80 | 12,24 | ||
| 9,66 | 10,96 | 4,46 | 14,13 | 9,94 | 8,97 | 5,06 | 13,30 | 11,04 | ||
| 0,44 | 4,95 | 12,22 | 9,84 | 4,75 | 17,20 | 15,53 | 8,05 | 14,51 | ||
| 7,04 | 9,13 | 12,35 | 6,43 | 8,22 | 5,55 | 7,61 | 11,52 | 16,88 | ||
| 14,97 | 9,83 | 10,69 | 14,46 | 12,82 | 9,11 | 10,02 | 7,60 | 15,50 | ||
| 3,89 | 9,10 | 13,08 | 14,71 | 11,40 | 8,14 | 4,96 | 9,13 | 14,89 | ||
| 10,72 | 8,04 | 9,90 | 5,56 | 8,56 | 11,16 | 13,51 | 13,31 | 10,04 | ||
| 4,06 | 4,95 | 9,76 | 9,17 | 4,58 | 6,40 | 8,94 | 12,89 | 10,13 | ||
| 9,30 | 9,13 | 6,51 | 11,65 | 19,58 | 5,59 | 9,55 | 9,81 | 11,97 | ||
| 13,78 | 3,06 | 6,71 | 9,13 | 16,10 | 6,62 | 10,65 | 11,72 | 9,85 | ||
| 11,75 | 5,82 | 7,57 | 6,05 | 8,58 | 8,19 | 13,24 | 9,75 | 8,20 | ||
| 9,36 | 13,84 | 3,93 | 16,59 | 7,24 | 6,44 | 16,42 | 4,37 | 15,17 | ||
| 5,42 | 8,64 | 8,70 | 8,77 | 7,85 | 8,87 | 7,23 | 12,24 | 11,88 | ||
| 4,99 | 7,74 | 9,80 | 6,47 | 7,61 | 11,10 | 5,11 | 14,05 | 7,57 | ||
| 6,11 | 7,04 | 12,28 | 16,78 | 9,60 | 12,23 | 12,20 | 10,37 | 9,12 | ||
| 7,97 | 6,45 | 8,57 | 15,24 | 8,82 | 10,38 | 14,32 | 7,58 | 21,46 | ||
| 7,71 | 7,08 | 6,51 | 8,72 | 8,09 | 4,81 | 10,66 | 7,08 | 15,25 | ||
| 11,02 | 5,65 | 13,81 | 10,91 | 12,09 | 9,96 | 8,92 | 7,21 | 10,36 | ||
| 6,11 | 11,26 | 10,92 | 10,27 | 10,16 | 2,96 | 13,92 | 9,93 | 12,33 | ||
| 5,55 | 11,19 | 10,72 | 14,50 | 14,08 | 9,91 | 14,37 | 9,28 | 16,22 | ||
| 6,28 | 4,09 | 5,58 | 4,85 | 13,70 | 9,03 | 9,17 | 10,13 | 15,34 | ||
| 13,18 | 7,87 | 18,82 | 15,14 | 10,46 | 10,51 | 16,19 | 17,30 | 19,21 | ||
| 12,75 | 4,03 | 11,29 | 8,86 | 10,52 | 9,18 | 12,25 | 7,19 | 10,53 | ||
| 10,19 | 13,31 | 16,10 | 11,51 | 5,24 | 12,13 | 12,98 | 9,85 | 7,20 | ||
| 4,85 | 11,45 | 9,33 | 6,86 | 12,81 | 15,59 | 4,69 | 15,35 | 15,95 | ||
| 7,94 | 11,22 | 7,94 | 13,40 | 8,88 | 3,08 | 3,61 | 16,88 | 12,51 | ||
| 9,13 | 8,90 | 6,31 | 14,37 | 8,96 | 16,64 | 11,87 | 10,96 | 17,15 | ||
| 12,95 | 5,98 | 5,98 | 11,48 | 7,51 | 7,57 | 6,13 | 7,56 | 10,40 | ||
| 7,44 | 7,52 | 17,77 | ||||||||
| γ1 = | 0,80 | γ1 = | 0,80 | γ1 = | 0,80 | |||||
| γ2 = | 0,90 | γ2 = | 0,85 | γ2 = | 0,95 |
Вариант 13 Вариант 14 Вариант 15
| 14,88 | 15,63 | 13,80 | 12,66 | 15,45 | 12,95 | 12,33 | 15,00 | 16,58 | ||
| 14,32 | 8,74 | 10,73 | 9,63 | 19,90 | 10,67 | 19,09 | 15,97 | 14,44 | ||
| 4,70 | 13,50 | 15,97 | 10,04 | 13,96 | 9,25 | 11,76 | 14,88 | 18,20 | ||
| 13,42 | 10,84 | 15,93 | 11,04 | 15,88 | 17,21 | 9,70 | 15,80 | 11,62 | ||
| 5,41 | 14,39 | 15,48 | 12,57 | 19,92 | 15,77 | 9,92 | 14,94 | 5,90 | ||
| 11,78 | 12,00 | 10,65 | 13,31 | 13,74 | 4,52 | 15,74 | 14,49 | 17,19 | ||
| 12,49 | 17,05 | 14,36 | 14,80 | 16,77 | 19,22 | 13,59 | 17,09 | 13,87 | ||
| 14,69 | 11,93 | 10,84 | 15,48 | 12,87 | 15,11 | 7,97 | 19,04 | 12,17 | ||
| 16,71 | 4,25 | 13,42 | 18,06 | 11,59 | 15,13 | 15,23 | 13,72 | 18,45 | ||
| 10,35 | 13,76 | 11,29 | 8,64 | 20,96
 Сейчас читают про:
|
 2018-01-08
2018-01-08 665
665





