Импульс релятивистской частицы. Уравнение движения релятивистской частицы

Релятивистское уравнение движения. Пусть имеются две ИСО XY иX'Y', движущиеся друг относительно друга. Причем система X'Y' является сопровождающей, т.е. в исследуемый момент времени тело в ней покоится. Масса тела m₀ в сопровождающей системе отсчета является массой покоя. Для системы X'Y' справедлив 2 закон Ньютона F' = m· a'. Вектора силы и ускорения и их проекции на нормальное n и тангенциальное t направления в сопровождающей СО изображены на рис. 14.1 (обозначения со штрихами). Исходя из 2 закона Ньютона и рис. 14.1, можно записать уравнение динамики относительно сопровождающей СО:

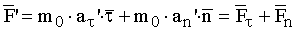. (14.1) 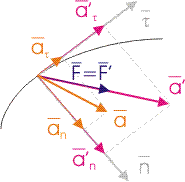рис.14.1

Найдем как будет выглядеть данное уравнение в системе отсчета XY, которую условно будем считать неподвижной. Используя соотношения (6.10-6.11), и учитывая, что a _t - продольная составляющая ускорения (направлена вдоль скорости движения сопровождающей СО), а a _n - поперечная составляющая ускорения, получим релятивистское уравнение, описывающее движение тела в системе XY:

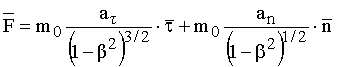, (14.2)
где b = V/c - отношение скорости движения сопровождающей СО к скорости света. Причем в этой СО скорость движения тела v равна скорости движения системы V.

Еще раз отметим, что поскольку нормальная и тангенциальная составляющие вектора ускорения a изменяются по-разному с изменением скорости движения сопровождающей СО, а вектора F и F ' равны и не зависят от скорости движения системы, то в общем случае вектора силы F и ускорения a не параллельны. Следовательно, 2 закон Ньютона в системе XYне выполняется.

Проведем дальнейшие преобразования уравнения (14.2). Поскольку вектора нормального и тангенциального ускорения рассчитываются, исходя из выражений (14.3)

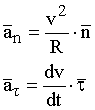, (14.3)

то уравнение (14.2) можно записать в виде:

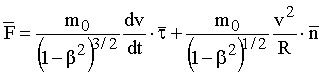. (14.4)

Проведем дальнейшие упрощения. Исходя из определения ускорения, имеем:

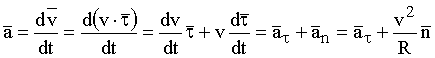. (14.5)

Следовательно,

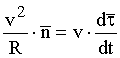. (14.6)

Кроме того, путем дифференцирования можно показать, что справедливо следующее выражение:

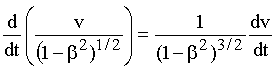. (14.7)

Используя выражения (14.6-14.7), уравнение (14.4) преобразуем к виду, которое представляет собой

релятивистское уравнение движения:

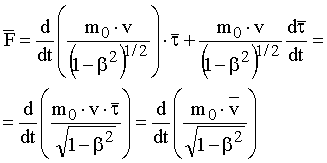. (14.8)

29 Закон сохранения энергии в релятивистском случае. Полная энергия и энергия покоя. Кинетическая энергия релятивистской частицы.

Закон сохранения энергии в релятивистском случае. Если частица движется только в поле консервативных сил, то работа на элементарном участке равна изменению потенциальной энергии системы, взятой с обратным знаком dA = - DE_п. Тогда уравнение (14.16) можно представить в виде:

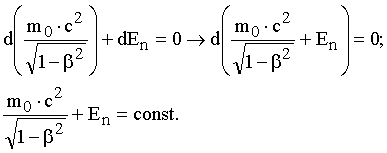. (14.18)