2018-01-08
554
| yt | 
| yt-
| ( )2
| 
|
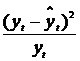
| 10,00 | 10,53 | 0,53 | 0,2809 | 0,0281 |
| 11,00 | 10,8 | 0,20 | 0,0400 | 0,0036 |
| 11,42 | 11,23 | 0,19 | 0,0361 | 0,0032 |
| 11,33 | 11,34 | 0,01 | 0,0001 | 0,0000 |
| 11,87 | 11,61 | 0,26 | 0,0676 | 0,0057 |
| 11,77 | 11,88 | 0,11 | 0,0121 | 0,0010 |
| 12,22 | 12,15 | 0,07 | 0,0049 | 0,0004 |
| 12,15 | 12,34 | 0,19 | 0,0361 | 0,0030 |
| 0,4778 |
.
Определяем среднюю относительную ошибку и корреляционное отношение (3.3) и (3.4)
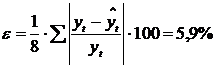
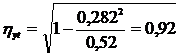
Расчеты показывают близость значений ryt и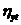 
, подтверждает правильность выбранной модели (незначительные расхождения в результате объясняются округлением).
Кроме того, близость 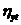к единице свидетельствует о надежности и сущности связи между yt и t.
Шаг 4. Прогнозирование показателя yt.
4.1 Расчет ограниченной оценки прогноза показателя 
осуществляем подстановкой величины ti = 9 в полученное уравнение тренда.
= 10,26 +0,27 * 9 = 12,69
4.2 Расчет интервальной оценки прогноза осуществляется по зависимости (4.1)
где 
- статистика Стьюдента по таблицам приложения в зависимости от к = n – 2 = 6 и уровне значимости 
.
Тогда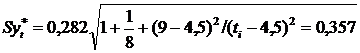 
.
Доверительный интервал прогноза показателя
|
|
|
То есть прогнозная величина будет находиться в интервале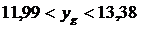 
.
Разработка сезонного прогноза
При прогнозировании экономических показателей, подверженных влиянию сезонных колебаний, возможно применение следующих способов:
1. Метода экстраполяции с учетом сезонности;
2. Гармоник ряда Фурье.
В первом случае, зная уравнение тренда и средние индексы сезонности, можно спрогнозировать последующие уровни ряда. В общем виде
(2.1)
Рассмотренная схема учета «сезонной волны» (умножение тренда на индекс сезонности) является мультипликативной.
Возможна и другая схема учета сезонной волны - аддитивная, когда к тренду прибавляется средняя величина абсолютных отклонений фактических уровней от выравненных
(2.2)
где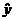 
- прогнозируемый уровень;
— теоретический уровень, рассчитанный по аналитической функции f(t).
Прогнозирование вторым методом проводят на основе гармонического анализа рядов динамики, который выполняют, представляя временной ряд как совокупность гармонических колебательных процессов. Для каждой точки этого ряда справедливо выражение (ряд Фурье)
(2.3)
В формуле (2.3) k определяет номер гармоники, который используется с различной степенью точности (обычно от 1 до 4). При решении уравнения (2.3) параметры определяются на основе положений метода наименьших квадратов.
Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, решение которой дает следующие формулы для вычисления параметров:
(2.4)
(2.5)
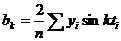(2.6)
При анализе ряда внутригодовой динамики по месяцам значение n принимается за 12. Представляя месячные периоды как части окружности, ряд внутригодовой динамики можно записать в таком виде:
|
|
|
Периоды ( )
| 0 |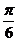 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
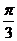
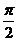
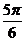
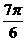
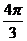
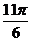
Уровни ( )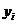
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | y12 |
Используем указанные методы для прогнозирования выработки энергии.
В первом случае найдем последующие уровни производства энергии, рассчитав выровненные по прямой значения показателя и скорректировав их на индексы сезонности.
Для прямолинейной функции 
параметры находятся из системы уравнений
(2.7)
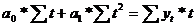
Полученная модель тренда имеет следующий вид
= -2,27* t + 546,02 (2.8)
Теоретические уровни и прогнозные значения показателя производства энергии, рассчитанные по модели (2.8) с учетом индексов сезонности представлены в таблице (табл. 2.1).
Таблица 2.1
