Момент импульса и закон его сохранения

 

Закон сохранения момента импульса

Рассмотрим частый случай вращательного движения, когда суммарный момент внешних сил равен нулю. При вращательном движении тела каждая его частица движется с линейной скоростью υ = ωr, [r, — радиус окружности, которую описыва­ет частица массой m, ω — угловая скорость, одинаковая для всех точек тела].

Момент импульса вращающегося тела равен сумме моментов

импульсов отдельных его частиц:

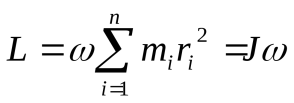(3.18)

Изменение момента импульса равно импульсу момента сил:

dL=d(Jω)=Jdω=Mdt (3.19)

Если суммарный момент всех внешних сил, действующих на систему тела относительно произвольной неподвижной оси, равен нулю, т.е. М=0, то dL и векторная сумма моментов импульсов тел системы не изменяется с течением времени.

Сумма моментов импульсов всех тел изолированной системы сохраняется неизменной (закон сохранения момента импульса):

d(Jω)=0 Jω=const (3.20)

Согласно закону сохранения момента импульса можно записать

J1ω1= J2ω2 (3.21)

где J1 и ω1 - момент инерции и угловая скорость в начальный момент времени, а и J2 и ω2 – в момент времени t.

Из закона сохранения момента импульса следует, что при М=0 в процессе вращения системы вокруг оси любое изменение расстояния от тел до оси вращения должно сопровождаться изменением скорости их обращения вокруг этой оси. С увеличением расстояния скорость вращения уменьшается, с уменьшением – возрастает. Например, гимнаст, совершающий сальто, чтобы успеть сделать в воздухе несколько оборотов, во время прыжка свёртывается клубком. Балерина или фигуристка, кружась в пируэте, разводит руки если хочет замедлить вращение, и, наоборот, прижимает их к телу, когда старается вращаться как можно быстрее.

 

Момент импульса

При сравнении законов поступательного и вращательного движений видна аналогия между ними. Во вращательном движении аналогом силы становится ее момент, аналог массы - момент инерции. Какая же величина будет аналогом импульса тела? Это момент импульса тела относительно оси. Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: 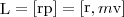где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Рис.1

Модуль вектора момента импульса 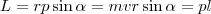где α - угол между векторами r и р, l - плечо вектора р относительно точки О. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z. При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса riсо скоростью vi. Скорость vi и импульс mivi перпендикулярны этому радиусу, т. е. радиус является плечом вектора mivi. Значит, мы можем записать, что момент импульса отдельной частицы равен 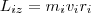(1) и направлен по оси в сторону, определяемую правилом правого винта. Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: 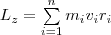Используя формулу vi = ωri, получим 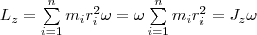т. е. 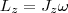2) Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени: т. е. 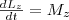Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Можно показать, что имеет место векторное равенство 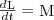(3) В замкнутой системе момент внешних сил 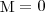и 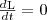откуда 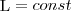(4) Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω1. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω2 увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.

Рис.2

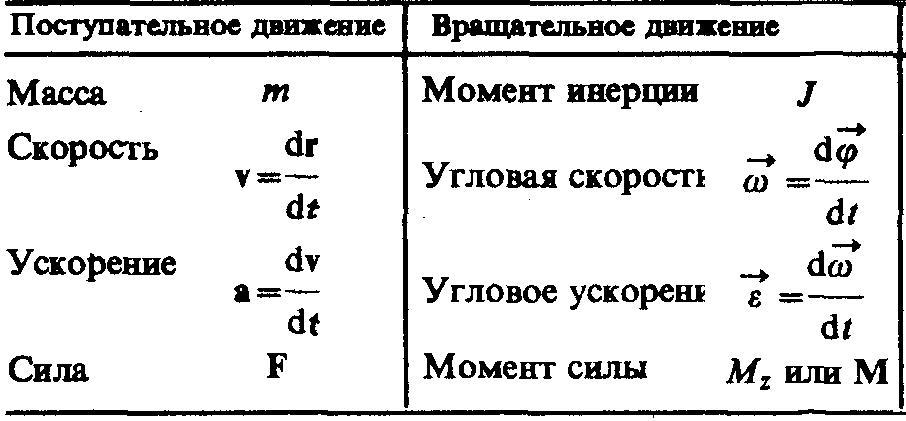
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (см таблицы ниже).

 

 

17.Работа и кинетическая энергия при вращательном движении твердого тела.

 

Работа и кинетическая энергия при вращательном движении твердого тела. @

‑ угол между векторамиaНайдем работу при вращательном движении твердого тела. Пусть ось враще­ния проходит через точку О, находящуюся на расстоянии r от точки приложения силы С, а 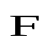и 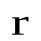.j) на величину этого смещения r da. Работа силы равна произведению проекции силы вдоль смещения Fsin(j точка приложения силы проходит путь dS=rdj(рис.3.5). При повороте тела на бесконечно малый уголd 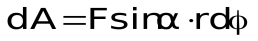) = M - момент силы. Таким образом:asin(×r×. НоF работа силы при вращении тела вокруг неподвижной оси равна произведе­нию момента действующей силы на угол поворота dA = Mdj.

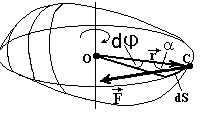Рис.3.5. Вычисление работы при вращательном движении твердого тела.

Чтобы рассчитать кинетическую энергию вращательного движения твердого тела, мысленно его разобьем наn материальных точек с массами m1, m2,...,mn, нахо­дящихся на расстояниях r1, r2,...,rn от оси вращения. Так как тело абсолютно твердое, уг­ловые скорости всех его точек одинаковы

.

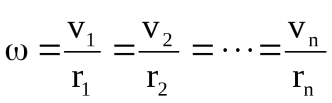Линейные скорости точек будут разные 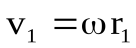, 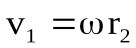и т.д. Кинетическая энергия вращающегося тела Ек.вр равна

;

.

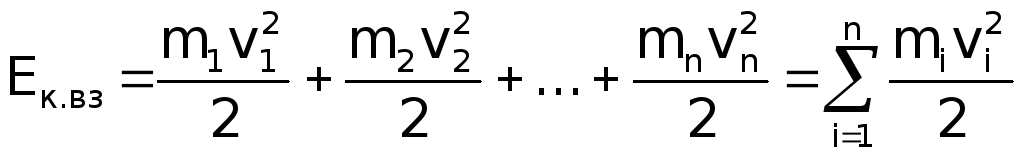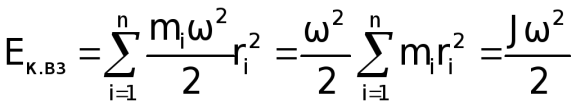Работа внешних сил при вращении тела идет на увеличение его кинетической энергии. dA=dЕк.вр, следовательно работу можно пред­ставить как разность кинети­че­ских энергий ко­нечного и начального положений

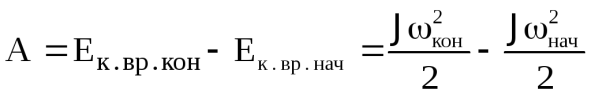
Если тело катится без скольжения, то оно одновременно участвует в двух дви­жениях: по­ступательном и вращательном, и его кинети­чес­кая энергия

.

 

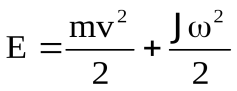18.Плоское движение тела, скатывающееся с наклонной плоскости без скольжения.

 

С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).

Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н» R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.

При качении цилиндра на него действуют три силы: сила тяжести 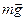, упругая сила реакции опоры 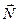и сила трения покоя 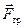(ведь качение без проскальзывания!).

Представим это движение суммой двух движений: поступательного со скоростью VC, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.

. (10.9)

Рис. 10.5

Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».

Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:

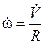, то есть .

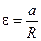Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:

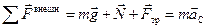. (10.10)

Для описания вращения воспользуемся основным уравнением динамики вращательного движения:

MC = IC × e. (10.11)

Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:

x: mgSina – Fтр = maC; (10.12)

y: N – mgсosa = 0. (10.13)

Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:

.

Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):

.

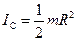Учитывая всё это, уравнение (10.11) перепишем так:

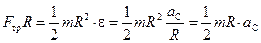. (10.14)

Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:

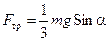; (10.15)

. (10.16)

Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя Fтр. Но, как известно, её рост ограничен предельным значением:

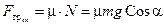. (10.17)

Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:

⅓mgSina ≤ mmgCosa.

Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения aпред