Функція 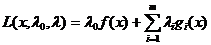 зветься узагальненою функцією Лагранжа, числа –
зветься узагальненою функцією Лагранжа, числа – 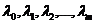 множники Лагранжа.
множники Лагранжа.
Класична функція Лагранжа має вигляд 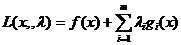 .
.
Градиєнтами узагальненої та класичної функцій Лагранжа по х є вектор-стовпець з частинними похідними першого порядку
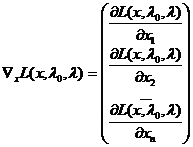 ,
, 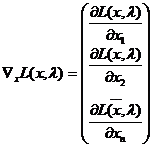 .
.
Другим диференціалом узагальненої та класичної функцій Лагранжа є
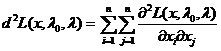 ,
, 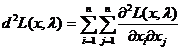 .
.
Першим диференціалом обмежень gj(x) є функція
 .
.
Результати досліджень локальних екстремумів в точці х* приводимо у таблиці 1.
Таблиця 1.
| № | 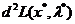
| 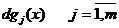
| Тип умовно-стаціонарної точки х* |
| >0 | 0, 
| Умовний локальний мінімум | |
| <0 | 0, 
| Умовний локальний максимум | |
| ≥0 | Може бути умовний локальний мінімум. Необхідні додаткові дослідження. | ||
| ≤0 | Може бути умовний локальний максимум. Необхідні додаткові дослідження. | ||
| = | Необхідні додаткові дослідження. | ||
| >0, <0 | Екстремуму немає. |
Приклад 1.
Знайти умовний екстремум функції за методом множників Лагранжа 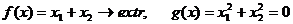 :
:
1. Перевіряємо умову регулярності. Так як 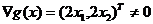 для усіх точок
для усіх точок  , то умова регулярності виконується. Тому, скористаємося класичною функцією Лагранжа.
, то умова регулярності виконується. Тому, скористаємося класичною функцією Лагранжа.
2. Скаладаємо функцію Лагранжа  .
.
3. Записуємо необхідні умови екстремуму першого порядку 3.1. 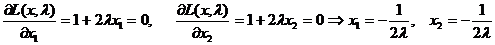 3.2.
3.2. 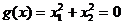 .
.
4. Рішенням системи є дві точки умовного екстремуму  .
.
5. Перевіряємо достатні умови екстремуму в точці А 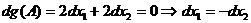 ,
,  <0, при
<0, при 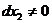 . Тому в точці А маємо умовний локальний максимум.
. Тому в точці А маємо умовний локальний максимум.
6. Перевіряємо достатні умови екстремуму в точці В 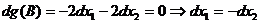 ,
,  >0, при
>0, при 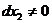 . Тому в точці В маємо умовний локальний мінімум.
. Тому в точці В маємо умовний локальний мінімум.
Задача 1
Визначити умовний екстремум функції за методом множників Лагранжа:
1.1. 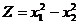
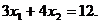
1.2. 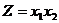
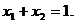
1.3. 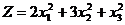

1.4. 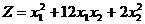

 2018-01-21
2018-01-21 572
572








