Теорема (існування й єдиність розв’язку задачі Коші рівняння, не розв’язаного відносно похідної)

Нехай у замкненому околі точки 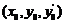функція 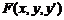задовольняє умовам:

1) 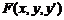- неперервна по всіх аргументах;

2) 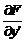існує і відмінна від нуля;

3) .

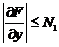Тоді при 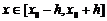, де 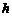- досить мало, існує єдиний розв’язок 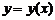рівняння 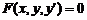, що задовольняє початковій умові .

Доведення. Як випливає з математичного аналізу відповідно до теореми про неявну функцію можна стверджувати, що умови 1) і 2) гарантують існування єдиної неперервної в околі точки 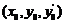функції 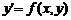, обумовленої рівнянням 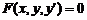, для якої 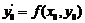. Перевіримо, чи задовольняє умові Ліпшиця чи більш грубій 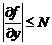. Диференціюєм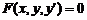о по . Оскільки 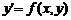, то одержуємо . 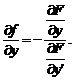Звідси З огляду на умови 2), 3), одержимо, що в деякому околі точки 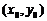буде 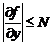і для рівняння 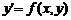виконані умови теореми існування й єдиності розв’язку задачі Коші.

2. Лінійні однорідні диференціальні рівняння з сталими коефіцієнтами. Побудова загального розв’язку.

Теорема. Загальним розв’язком лінійного однорідного рівняння

є лінійна комбінація 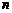- лінійно незалежних розв’язків .

Доведення. Оскільки є розв’язками, то в силу третьої властивості їхня лінійна комбінація також буде розв’язком. Покажемо, що цей розв’язок загальний, тобто вибором сталих 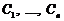можна розв’язати довільну задачу Коші 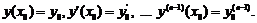Дійсно, оскільки система розв’язків лінійно незалежна, то визначник Вронського відмінний від нуля й алгебраїчна система неоднорідних рівнянь

має єдиний розв’язок 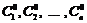. І лінійна комбінація 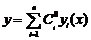є розв’язком, причому, як видно із системи алгебраїчних рівнянь, буде задовольняти довільно обраним умовам Коші.

Властивість. Максимальне число лінійно незалежних розв’язків дорівнює порядку рівняння.

Це випливає з попередньої теореми, тому що будь-який розв’язок виражається через лінійну комбінацію 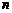- лінійно незалежних розв’язків.

Визначення. Будь-які 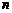-лінійно незалежних розв’язків лінійного однорідного рівняння 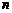-го порядку називаються фундаментальною системою розв’язків.