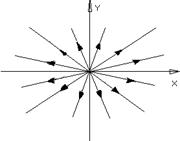
Розглянемо лінійну стаціонарну систему диференціальних рівнянь на площині
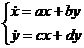
Побудуємо якісну картинку наведеного розв‘язку  в залежності від параметрів системи (побудування фазового портрету). При розв‘язку системи складаємо характеристичне рівняння
в залежності від параметрів системи (побудування фазового портрету). При розв‘язку системи складаємо характеристичне рівняння 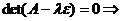
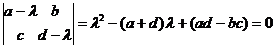
I. Нехай 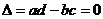 . Тоді корені характеристичного рівняння
. Тоді корені характеристичного рівняння 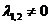
1) Нехай 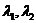 –дійсні, різні, одного знаку
–дійсні, різні, одного знаку
a) 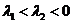 . Розв‘язок має вигляд:
. Розв‘язок має вигляд:
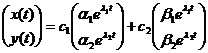
де 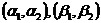 – власні вектори. При
– власні вектори. При 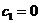 :
:
 , або
, або 
 Траекторія має вигляд прямої. І оскільки
Траекторія має вигляд прямої. І оскільки
 , то рух по ній
, то рух по ній  при
при 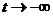 .
.
Аналогічно при  :
:
 , або
, або 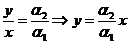
І оскільки 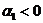 , то
, то  при
при 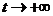 .
.
Траекторії між цими прямими мають вигляд “парабол” і оскільки  , то рух направлен до початку координат. Точка рівноваги називається “стійким вузлом”.
, то рух направлен до початку координат. Точка рівноваги називається “стійким вузлом”.
б) Нехай 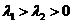 .
.
 Оскільки при заміні
Оскільки при заміні  все залишиться,
все залишиться,
як і в попередньому випадку, то фазовий
портрет цієї системи відрізняється від попереднього
лише напрямом руху. Тобто
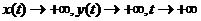 . Степінь рівноваги назвемо
. Степінь рівноваги назвемо
“нестійким вузлом”.
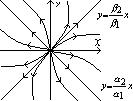
2) Нехай 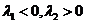 , дійсні, різних знаків.
, дійсні, різних знаків.
Загальний розв‘язок 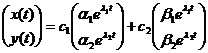
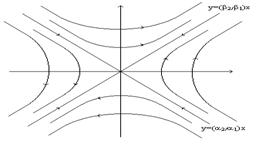

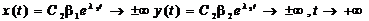 При c1=0 маємо І рух іде по прямій y=(b2/b1)x. При c2=0 маємо
При c1=0 маємо І рух іде по прямій y=(b2/b1)x. При c2=0 маємо
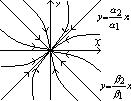
Всі інші траєкторії мають
вигл. “гіпербол”, розташованих
між цими прямими. Рух по траєктор.
збіг. до до однієї прямої і розбіг. від

іншої. Стан рівноваги наз “сідлом”, а прямі відповідно стійкою і постійною сепаратрисами. 3) Нехай корені комплексні l1,2=p±iq Розв. має вигл.
а) Нехай p<0 Тоді x(t)®0 y(t)®0 при t® µ при чому траєкторії мають вигл. спіралей, що “накручуються” на поч. корд. Стан рівноваги наз “стійким фокусом”.
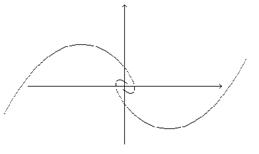 б) Нехай p>0 траєкторія зберіг. такий же вигл. але рух іде у протил. напр. Стан рівноваги наз “нестійким фокусом”.
б) Нехай p>0 траєкторія зберіг. такий же вигл. але рух іде у протил. напр. Стан рівноваги наз “нестійким фокусом”.
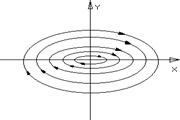 4. Нехай λ1,2=±iq. Розв’язок має вигляд:
4. Нехай λ1,2=±iq. Розв’язок має вигляд: 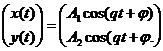
Траєкторії мають вигляд замкнених кривих. Рух по них
періодичний  .Стан рівноваги називається
.Стан рівноваги називається
”центром”.
5. Нехай корені кратні, l1=l2=l. Можливі 2 випадки:
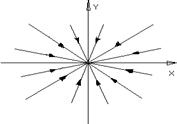 1)Матриця Жордана має вигляд
1)Матриця Жордана має вигляд 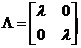 . Тоді розвязок має вигляд x(t)=C1elt, y(t)= C2elt,або
. Тоді розвязок має вигляд x(t)=C1elt, y(t)= C2elt,або 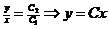 .
.
а)Якщо l<0,то стан рівноваги називається стійким дикритичим вузлом.
б)Якщо l>0,то нестійкий дикритичний вузол.
2)Якщо клітина Жордана 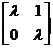 ,то
,то 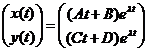 .Інтегральні криві мають вигляд “парабол”,що злиплись однією стороною.
.Інтегральні криві мають вигляд “парабол”,що злиплись однією стороною.
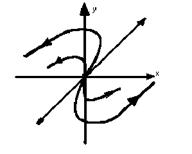
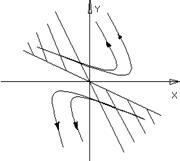
а) Якщо l<0,то стан рівноваги називається стійким виродженим вузлом.
б) Якщо a >0,то стан рівноваги наз. нестійким ви-
дженим вузлом.
ІІ Нехай D=ad-bc=0. Тоді характеристичне рівняння
має вигляд:l2 –(a+d)l=0.
l1=0 l2=a+d.
1) Нехай l1=0, l2= a+d ¹ 0. Загальний розв’язок
x(t)=C1a1el1t +C2b1
y(t)= C1a2el2t +C2b2
 Система xْ =ax+by
Система xْ =ax+by
yْ=cx+dy може бути переписана 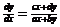
Оскільки 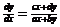 , то строки пропорційні і (cx+dy)=α(ax+by),звідки
, то строки пропорційні і (cx+dy)=α(ax+by),звідки

Оскільки на прямій ax+by=0 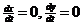 , то це пряма сталих точок.
, то це пряма сталих точок.
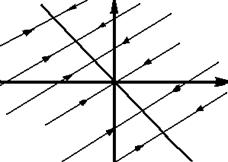
А на сім’ї прямих y=αx+C рух йде за законом x(t)=C1a1elt,y(t)= C2a2elt
a) якщо l<0,то особлива пряма—стійка.
 |
b) якщо l>0,то особлива пряма нестійка.
 |
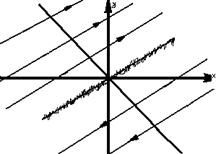
2)Нехай l1=l2=0, тоді особлива пряма ax+by=0 співпадає з однією з сім’ї y=αx+C,тобто
з y=αx.
СТІЙКІСТЬ ЛІНІЙНИХ СИСТЕМ В R  .
.
Розглянемо систему лінійних неоднорідних диференційних рівнянь 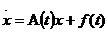 .Нехай
.Нехай  -
-
розв’язок,що досліджується на стійкість.
ТЕОРЕМА.
Дослідження стійкості довільного розв’язку  лінійної неоднорідної системи еквівалентна дослідженню стійкості нульового розв’язку
лінійної неоднорідної системи еквівалентна дослідженню стійкості нульового розв’язку 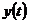
 .відповідної однорідної системи
.відповідної однорідної системи 

ДОВЕДЕННЯ:
Зробимо заміну 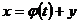 ,де
,де 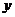 - нова невідома функція.Одержимо
- нова невідома функція.Одержимо 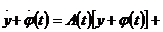
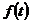 .
.
Поскільки 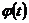 -розв’язок,то
-розв’язок,то 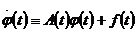 .І залишиться однорідна система
.І залишиться однорідна система 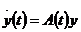 .Як видно
.Як видно
з вигляду заміни 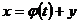 розв’язку
розв’язку  відповідає
відповідає 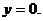
ЗАУВАЖЕННЯ
На стійкість довільного розв’язку  впливає лише матриця
впливає лише матриця 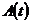 ! І всі розв’язки лінійних неодно-
! І всі розв’язки лінійних неодно-
рідних систем одночасно або стійкі або нестійкі,в залежності від стійкості нульового розв’язку одно-
рідної системи.
Таким чином (на відміну від нелінійних систем) справедливе визначення.
ВИЗНАЧЕННЯ
Лінійна система називається стійкою (асимптотично стійкою) якщо є стійкими (асимптотично стійки- ми) всі її розв’язки.
Розглянемо лінійні системи з сталими коефіцієнтами 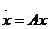 .Умови стійкості для цих систем мають
.Умови стійкості для цих систем мають
найбільш конструктивний вигляд.При дослідженні складається характеристичне рівняння det(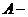
- 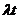 )=0,або
)=0,або 
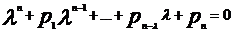 .Нехай
.Нехай 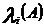 ,
, 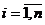
 власні числа матриці
власні числа матриці  ,тобто коре-
,тобто коре-
ні характеристичного рівняння.
ТЕОРЕМА
1.Щоб лінійна стаціонарна система була асимптотично стійкою необхідно і достатньо,щоб 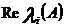 <0,
<0, 
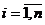 .
.
2.Щоб лінійна стаціонарна система була стійкою за Ляпуновим необхідно і достатньо,щоб

Причому з нульовою дійсною частиною 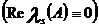 мали прості елементарні дільники,або клітка
мали прості елементарні дільники,або клітка
Жордана складалася з одного елементу.
3.Якщо існує хоч один корінь 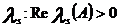 ,то система нестійка.
,то система нестійка.
ДОВЕДЕН якщо λ1= λ2=... λn= λ кратні корені.
Звідси видно, що при Re λi (А)<0 то незал. від кратності |x(t)|→0, t→+∞.
Якщо Re λi (A)=0 то комплексні корені стійкості не заважають.але потрібна відсутність многочлена(t).це забезпечуеться простотою елемент. дільн.►
Таким чином,при досліджені стійкості розкрив. хар. рів.det(A- λE)=0 і дослідж. корені λi(А).
Як виплив з теор корені можна не знати,досить визначити значен дійсної частини Re λi (A).
Існують алгебраічні та частотні критерії.
Нех. хар. рів. має вигляд:
λⁿ +p1λⁿֿ¹+p2 λⁿֿ ²+...+pn-1λ+pn=0 Матриця виглядає:
│ p1 1 0 0 …0│
Г= │ p3 p2 p1 1… 0│ - матриця Гурвіца, де рi=0 якщо і>n.
│......... …. …… │
│ p2n-1 p2n-2 ……… pn│
 2018-01-21
2018-01-21 860
860








