1. Абсолютный покой жидкости. Рассмотрим равновесие жидкости в состоянии абсолютного покоя, т.е. когда на жидкость действует только сила тяжести. Давление на свободную поверхность жидкости равно атмосферному давлению  . Определим давление
. Определим давление  в произвольно выбранной точке М, расположенной на глубине
в произвольно выбранной точке М, расположенной на глубине  (рис. 1.3). Для этогорассмотрим равновесие жидкого тела, ограниченного снизу площадкой
(рис. 1.3). Для этогорассмотрим равновесие жидкого тела, ограниченного снизу площадкой 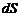 . Давление на основание выделенного объема будет внешним по отношению к жидкому телу и будет направлено вертикально вверх. Запишем уравнение равновесия в проекции на вертикальную ось тела:
. Давление на основание выделенного объема будет внешним по отношению к жидкому телу и будет направлено вертикально вверх. Запишем уравнение равновесия в проекции на вертикальную ось тела:
 , т.е.
, т.е.  . (1.16)
. (1.16)
Получили основное уравнение гидростатики.
 Давление во всех точках свободной поверхности одинаково и равно
Давление во всех точках свободной поверхности одинаково и равно  ,следовательно, давление во всех точках жидкости на глубине h также одинаково согласно основному уравнению гидростатики. Поверхность, давление на которой постоянно, называется поверхностью уровня. В данном случае поверхности уровня – горизонтальные плоскости. Выберем горизонтальную отсчетную плоскость, проходящую на расстоянии
,следовательно, давление во всех точках жидкости на глубине h также одинаково согласно основному уравнению гидростатики. Поверхность, давление на которой постоянно, называется поверхностью уровня. В данном случае поверхности уровня – горизонтальные плоскости. Выберем горизонтальную отсчетную плоскость, проходящую на расстоянии  от свободной поверхности, тогда уравнение (1.16) приобретает вид
от свободной поверхности, тогда уравнение (1.16) приобретает вид
 или
или  . (1.17)
. (1.17)
Все члены уравнения (1.17) имеют линейную размерность и носят название: 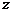 – геометрическая высота,
– геометрическая высота,  – пьезометрическая высота. Величина
– пьезометрическая высота. Величина  называется гидростатическим напором и согласно (1.17) при абсолютном покое жидкости постоянна.
называется гидростатическим напором и согласно (1.17) при абсолютном покое жидкости постоянна.
2. Относительный покой жидкости. Состояние равновесия жидкости при наличии переносного движения называется относительным покоем жидкости. Относительный покой сводится к двум возможным видам равновесия жидкости.
Равновесие жидкости при равномерно ускоренном прямолинейном
движении сосуда
Примером может служить равновесие жидкости в цистерне, движущейся с некоторым ускорением  (рис. 1.4, а). В этом случае на жидкость будут действовать сила тяжести и сила инерции равномерно укоренного движения цистерны:
(рис. 1.4, а). В этом случае на жидкость будут действовать сила тяжести и сила инерции равномерно укоренного движения цистерны:
 ,
,
где  – равнодействующая единичная массовая сила,
– равнодействующая единичная массовая сила,  – единичная массовая сила переносного движения.
– единичная массовая сила переносного движения.


а б
Рис. 1.4. К выводу основного уравнения гидростатики для относительного покоя:
а – равномерно ускоренное прямолинейное движение сосуда; б – равномерное
вращение сосуда
При движении цистерны начальное положение свободной поверхности жидкости изменится. Так как равнодействующий вектор массовых сил должен быть направлен по внутренней нормали к свободной поверхности жидкости, то новое положение свободной поверхности жидкости будет перпендикулярно вектору  . Наклон свободной поверхности жидкости к горизонтальной плоскости определяется соотношением ускорений
. Наклон свободной поверхности жидкости к горизонтальной плоскости определяется соотношением ускорений  :
:  .
.
Найдем условия равновесия жидкого объема, имеющего в основании малую площадку 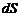 в точке М, расположенной внутри жидкости на глубине
в точке М, расположенной внутри жидкости на глубине  под уровнем свободной поверхности:
под уровнем свободной поверхности:
 , или
, или  .
.
Здесь  (h – погружение точки М под уровень свободной поверхности жидкости, измеряемое по вертикали), так как
(h – погружение точки М под уровень свободной поверхности жидкости, измеряемое по вертикали), так как  ,
,  . Приходим к уравнению равновесия жидкости
. Приходим к уравнению равновесия жидкости
 ,
,
совпадающему по виду с записью основного закона гидростатики (1.16).
Таким образом, давление в любой точке жидкости будет зависеть только от положения этой точки относительно уровня свободной поверхности жидкости. Поверхности равного давления будут параллельны свободной поверхности жидкости и иметь такой же уклон  .
.
Равновесие жидкости в равномерно вращающемся сосуде
Свободная поверхность жидкости, залитой в цилиндрический сосуд и находящейся под действием сил тяжести, примет форму горизонтальной плоскости на некотором уровне  относительно дна сосуда. После того как мы приведем сосуд во вращение вокруг его вертикальной оси с некоторой постоянной угловой скоростью
относительно дна сосуда. После того как мы приведем сосуд во вращение вокруг его вертикальной оси с некоторой постоянной угловой скоростью  const, форма свободной поверхности жидкости изменится: в центре сосуда уровень понизится, а по краям сосуда повысится, вследствие действия силы инерции, создающей ускорение переносного движения
const, форма свободной поверхности жидкости изменится: в центре сосуда уровень понизится, а по краям сосуда повысится, вследствие действия силы инерции, создающей ускорение переносного движения  , направленное в сторону стенок сосуда (рис. 1.4, б).
, направленное в сторону стенок сосуда (рис. 1.4, б).
Выберем любую точку жидкости на глубине под свободной поверхностью  (в частности, точка находится на дне сосуда), тогда давление в ней будет
(в частности, точка находится на дне сосуда), тогда давление в ней будет
 .
.
Этот вывод можно распространить и на более сложные случаи вращения сосуда. Наклоняя ось его вращения под углом к горизонту, результат получим тот же, что подтверждает универсальность основного уравнения гидростатики.
Пример 1.3. Найти форму поверхности жидкости во вращающемся сосуде (рис. 1.4, б).
Решение. В каждой точке поверхности вектор углового ускорения  будет направлен под некоторым углом
будет направлен под некоторым углом 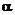 по отношению к касательной плоскости, проходящей через данную точку свободной поверхности:
по отношению к касательной плоскости, проходящей через данную точку свободной поверхности:
 ,
,
или после интегрирования
 ,
,
где  – координата самой низкой точки, расположенной в центре на оси вращения. Итак, получили, что свободная поверхность жидкости, находящейся в равномерно вращающемся вокруг его вертикальной оси сосуде, будет иметь вид параболоида вращения.
– координата самой низкой точки, расположенной в центре на оси вращения. Итак, получили, что свободная поверхность жидкости, находящейся в равномерно вращающемся вокруг его вертикальной оси сосуде, будет иметь вид параболоида вращения.
Пример 1.4. Конструкция подводного аппарата выдерживает избыточное давление до 10 МПа. Определить максимальную рабочую глубину погружения аппарата.
Решение. Из основного уравнения гидростатики имеем
 ,
,
т. е.  10×106/(998×9.81) = 1021 м.
10×106/(998×9.81) = 1021 м.
Дифференциальные уравнения
равновесия жидкости
Рассмотрим условия равновесия объема жидкости малых размеров в виде параллелепипеда (рис. 1.5).
Пусть на объем действует массовая сила  На левую и правую грани параллелепипеда действуют силы давления
На левую и правую грани параллелепипеда действуют силы давления  и
и  соответственно. На переднюю и заднюю грани:
соответственно. На переднюю и заднюю грани:  и
и  , на нижнюю и верхнюю грани:
, на нижнюю и верхнюю грани:  и
и  . Уравнения равновесия выделенного объема жидкости имеют вид:
. Уравнения равновесия выделенного объема жидкости имеют вид:
 ,
,
 ,
,
 ,
,
или
 .
.
Здесь
 ,
,
и аналогично для других направлений. Проекции массовой силы на координатные оси:
 ,
,
 ,
,
 ,
,
где 
 и
и  – соответствующие проекции ускорения.
– соответствующие проекции ускорения.

Рис. 1.5. К выводу уравнений равновесия
жидкости
В итоге получаем систему дифференциальных уравнений гидростатики (уравнения Эйлера):
 ,
,
 ,
,
 ,
,
или в векторной форме
 , (1.18)
, (1.18)
где  – поле массовых сил,
– поле массовых сил,  – дифференциальный оператор.
– дифференциальный оператор.
Из (1.18), в частности, следует, что приращение (полный дифференциал) давления при изменении координат жидкой частицы на  равно
равно
 . (1.19)
. (1.19)
Если из массовых сил на жидкость действует только сила тяжести, направленная вдоль оси 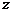 , то
, то  0,
0,  и уравнение (1.19) приобретает вид
и уравнение (1.19) приобретает вид
 . (1.20)
. (1.20)
Отсюда интегрированием получаем основное уравнение гидростатики. Рассмотрим пример равновесного состояния газа в поле сил тяжести.
 2018-02-14
2018-02-14 1634
1634
