2018-02-14
526
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид: 
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так: 
, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c: 
Математи́ческийма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Период малых колебаний математического маятника длины l в поле тяжести с ускорением свободного падения g приближенно равен 
и мало зависит от амплитуды и массы маятника.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида 
, где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах;
, где l ― длина подвеса, g ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: 
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;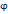 
— начальный угол отклонения маятника; 
— масса маятника; 
— расстояние от точки подвеса до центра тяжести маятника; 
— радиус инерции относительно оси, проходящей через центр тяжести. 
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса: 
.
Дифференциальное уравнение движения физического маятника
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом: 
. Полагая 
, предыдущее уравнение можно переписать в виде: 
. Последнее уравнение аналогично уравнению колебаний математического маятника длиной 
. Величина называется приведённой длиной физического маятника. Период малых колебаний физического маятника 
