Гауссовское (нормальное) распределение ошибок в линейной модели наблюдений 6 страница

И здесь при увеличении количества объясняющих переменных первое слагаемое в правой части уменьшается, а второе увеличивается. Среди нескольких альтернативных моделей (полной и редуцированных) предпочтение отдается модели с наименьшим значением .

Пример. В последнем примере получаем для полной модели и редуцированных моделей и следующие значения и .

	AIC	SC
M1	8.8147	8.9594
M2	8.6343	8.7428
M3	8.4738	8.5462

Предпочтительной по обоим критериям оказывается опять модель .

Замечание. В рассмотренном примере все три критерия , и выбирают одну и ту же модель. В общем случае подобное совпадение результатов выбора вовсе не обязательно.

Включение в модель большого количества объясняющих переменных часто приводит к ситуации, которую называют мультиколлинеарностью.

Мы обещали ранее коснуться проблемы мультиколлинеарности и сейчас выполним это обещание. Прежде всего напомним наше предположение

(4) матрица X^TX невырождена, т. е. ее определитель отличен от нуля:

которое можно заменить условием

(4^’) столбцы матрицы X линейно независимы.

Полная мультиколлинеарность соответствует случаю, когда предположение (4) нарушается, т. е. когда столбцы матрицы линейно зависимы, например,

( -й столбец является линейной комбинацией остальных столбцов матрицы ). При наличии чистой мультиколлинеарности система нормальных уравнений не имеет единственного решения, так что оценка наименьших квадратов для вектора параметров (коэффициентов) попросту не определена однозначным образом.

На практике, указывая на наличие мультиколлинеарности, имеют в виду осложнения со статистическими выводами в ситуациях, когда формально условие (4) выполняется, но при этом определитель матрицы X^TX близок к нулю. Указанием на то, что -я объясняющая переменная «почти является» линейной комбинацией остальных объясняющих переменных, служит большое значение коэффициента возрастания дисперсии

оценки коэффициента при этой переменной вследствие наличия такой «почти линейной» зависимости между этой и остальными объясняющими переменными. Здесь - коэффициент детерминации при оценивании методом наименьших квадратов модели

Если , то , и это соответствует некоррелированности -ой переменной с остальными переменными. Если же , то тогда , и чем больше корреляция -ой переменной с остальными переменными, тем в большей мере возрастает дисперсия оценки коэффициента при -ой переменной по сравнению с минимально возможной величиной этой оценки.

Мы можем аналогично определить коэффициент возрастания дисперсии оценки коэффициента при -ой объясняющей переменной для каждого :

Здесь — коэффициент детерминации при оценивании методом наименьших квадратов модели линейной регрессии -ой объясняющей переменной на остальные объясняющие переменные. Слишком большие значения коэффицентов возрастания дисперсии указывают на то, что статистические выводы для соответствующих объясняющих переменных могут быть весьма неопределенными: доверительные интервалы для коэффициентов могут быть слишком широкими и включать в себя как положительные, так и отрицательные значения, что ведет в конечном счете к признанию коэффициентов при этих переменных статистически незначимыми при использовании - критериев.

Пример. Обращаясь опять к данным об импорте товаров и услуг во Францию, находим:

Коэффициенты возрастания дисперсии для переменных и совпадают вследствие совпадения коэффициентов детерминации регрессии переменной на переменные и и регресии переменной на переменные и (взаимно обратные регрессии).

Полученные значения коэффициентов возрастания дисперсий отражают очень сильную коррелированность переменных и . (Выборочный коэффициент корреляции между этими переменными равен .)

При наличии мультиколлинеарности может оказаться невозможным правильное разделение влияния отдельных объясняющих переменных. Удаление одной из переменных может привести к хорошо оцениваемой модели. Однако оставшиеся переменные примут на себя дополнительную нагрузку, так что коэффициент при каждой из этих переменных измеряет уже не собственно влияние этой переменной на объясняемую переменную, а учитывает также и часть влияния исключенных переменных, коррелированных с данной переменной.

Пример. Продолжая последний пример, рассмотрим редуцированные модели, получамые исключением из числа объясняющих переменных переменной или переменной . Оценивание этих моделей приводит к следующим результатам:

c и для коэффициента при ;

c и для коэффициента при .

В каждой из этих двух моделей коэффициенты при и имеют очень высокую статистическую значимость. В первой модели изменчивость переменной объясняет изменчивости переменной ; во второй модели изменчивость переменной объясняет изменчивости переменной . С этой точки зрения, переменные и вполне заменяют друг друга, так что дополнение каждой из редуцированных моделей недостающей объясняющей переменной практически ничего не добавляя к объяснению изменчивости (в полной модели объясняется изменчивости переменной ), в то же время приводит к неопределенности в оценивании коэффициентов при и .

Но коэффициент при в полной модели соответствует связи между переменными и , очищенными от влияния переменной , тогда как коэффициент при в полной модели соответствует связи между переменными и , очищенными от влияния переменной . Поэтому неопределенность в оценивании коэффициентов при и в полной модели по-существу означает невозможность разделения эффектов влияния переменных и на переменную .

Приведем значения , и для всех трех моделей.


Полная	0.9702	1.1324	3.274	3.411
Без	0.9704	1.1286	3.211	3.303
Без	0.9719	1.0991	3.158	3.250

Все четыре критерия выбирают в качестве наилучшей модель с исключенной переменной .

Мы не будем далее углубляться в проблему мультиколлинеарности, обсуждать другие ее последствия и возможные способы преодоления затруднений, связанных с мультиколлинеарностью. Заинтересованный читатель может обратиться по этому вопросу к более полным руководствам по эконометрике.

2.10. ПРОВЕРКА ГИПОТЕЗ О ЗНАЧЕНИЯХ
КОЭФФИЦИЕНТОВ: ОДНОСТОРОННИЕ КРИТЕРИИ

Вспомним пример с потреблением текстиля. Мы подобрали линейную модель в логарифмах (с постоянными эластичностями)

(здесь — расходы на личное потребление текстиля, — относительная цена текстиля, - располагаемый доход). В рамках этой модели представляют интерес гипотезы и о «единичной эластичности» расходов на потребление текстиля как по доходам, так и по ценам.

Построить критерии с уровнем значимости для проверки этих гипотез можно по той же схеме, по которой строятся критерии проверки гипотез , только теперь для проверки гипотезы следует использовать - статистику

а для проверки гипотезы — - статистику

Каждая из этих статистик, в случае справедливости соответствующей нулевой гипотезы, имеет распределение . Нулевая гипотеза отвергается, если значение - статистики превышает по абсолютной величине значение .

В нашем примере

Таким образом, отклонение значения от гипотетического значения статистически значимо — гипотеза отвергается. В то же время, отклонение значения от гипотетического значения не является статистически значимым, и гипотеза не отвергается.

Замечание. Из проведенного рассмотрения видна важность не толькоабсолютных отклонений оценок от гипотетических значений параметров , но и точностей оценок , измеряемых дисперсиями и оцениваемых величинами . Действительно, абсолютные величины отклонений в рассмотренном примере равны

и ,

соответственно, т. е. отличаются не очень существенно. Однако примерно в 4.3 раза меньше, чем , и именно такое большое отличие и и приводит, в конечном счете, к противоположным решениям в отношении гипотез и .

Итак, на основании построенной процедуры гипотеза отвергается. А что же тогда принимается?

Формально, альтернативой для в построенном критерии является гипотеза , поскольку критическое множество содержит в равной степени как большие положительные, так и большие (по абсолютной величине) отрицательные значения - статистики . В то же время, значение , соответствующее отклонению , скорее говорит в пользу того, что в действительности .

В этой связи, естественным представляется более определенный выбор альтернативной гипотезы, а именно, сопоставление нулевой гипотезе односторонней альтернативы (односторонняя альтернатива — в отличие от двухсторонней альтернативы ). При такой постановке задачи отвержение нулевой гипотезы в пользу альтернативы производится только при больших положительных отклонениях , т. е. при больших положительных значениях -статистики. Если мы отнесем к последним значения, превышающие , то получим статистический критерий, у которого ошибка первого рода (уровень значимости) равна . Его критическое множество определяется соотношением

справа стоит теперь значение , а не , как это было при двухсторонней альтернативе. Поскольку у нас , мы отвергаем гипотезу в пользу гипотезы .

Построим аналогичную процедуру для параметра . Именно, построим критерий уровня для проверки гипотезы против односторонней альтернативы . Критическое множество такого критерия должно состоять из значений -статистики, превышающих . У нас значение

опять меньше порогового, так что гипотеза не отвергается в пользу .

Обратим теперь внимание на то, что при рассмотрении пары конкурирующих гипотез

мы выделяем в гипотезу только одно частное значение , хотя по-существу дела проблема состоит скорее в выборе между гипотезами

Последняя ситуация коренным образом отличается от предыдущей: оказывается сложной гипотезой, т. е. гипотезой, допускающей более одного значения параметра, в данном случае даже бесконечно много значений параметра . В противоположность этому, в предыдущей ситуации гипотеза была простой.

Какие осложнения возникают при использовании сложной нулевой гипотезы?

Возьмем, для примера, частную гипотезу . Мы отвергли бы ее в пользу при

В то же время, частную гипотезу мы отвергаем в пользу той же при

Иначе говоря, при различных частных гипотезах, входящих в состав сложной нулевой гипотезы , мы получаем различныекритические множества, обеспечивающие заданный уровень значимости (ошибку 1-го рода) . Построение каждого такого множества непосредственно использует конкретное гипотетическое значение , тогда как в рамках гипотезы отдельное гипотетическое значение параметра не конкретизируется.

Возникающее затруднение преодолевается, исходя из следующих соображений. Коль скоро мы не в состоянии построить единое для всех критическое множество, вероятность попадания в которое равна 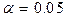при справедливости каждой отдельной частной гипотезы, следует попытаться построить единое для всех критическое множество, вероятность попадания в которое при выполнении каждой отдельной частной гипотезы была бы не больше 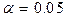. Такая задача реализуется путем использования критического множества, соответствующего граничному значению односторонней гипотезы, в данном случае .