График функции - множество точек, у которых абcциссы являются допустимыми значениями аргумента x, а ординаты - соответствующими значениями функции y.
 Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т.0 (y = ax - прямая пропорциональность)
Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т.0 (y = ax - прямая пропорциональность)
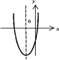 Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0
Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0
 Гипербола - график функции
Гипербола - график функции 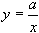 . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а > 0) или у - х (а < 0).
. При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а > 0) или у - х (а < 0).
 Логарифмическая функция y = logax (a > 0)
Логарифмическая функция y = logax (a > 0)
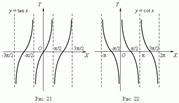
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком (рис. 19). Эта кривая называется синусоидой.
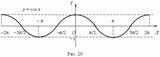
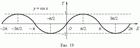 График функции y = cos x представлен на рис. 20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на
График функции y = cos x представлен на рис. 20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на  /2.
/2.
Основные свойства функций. Монотонность, четность, нечетность, периодичность функций.
Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f (x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.2 ) Нуль функции - такое значение аргумента, при котором значение функции равно нулю.3 ) Промежутки знакопостоянства функции - такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.4 ) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.5 ) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f (-x) = f (x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f (-x) = - f (x). График нечетной функции симметричен относительно начала координат.6 ) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f (x) | ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная. 7 ) Периодическость функции. Функция f (x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f (x+T) = f (x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Периодические функции. Правила нахождения основного периода функции.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Все тригонометрические функции являются периодическими. Являются неверными утверждения относительно суммы периодических функций: Сумма 2 функций с соизмеримыми (даже основными) периодами T 1 и T 2 является функция с периодом НОК (T 1, T 2). Сумма 2 непрерывных функций с несоизмеримыми (даже основными) периодами является непериодической функцией. Не существует периодических функций, не равных константе, у которой периодами являются несоизмеримые числа.
Построение графиков степенных функций.
Степенная функция. Это функция: y = axn, где a, n - постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу; при n = 1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, при n = 0 степенная функция превращается в постоянную величину: y = a, т. e. её график - прямая линия, параллельная оси Х, исключая начало координат (поясните, пожалуйста, почему?). Все эти случаи (при a = 1) показаны на рис.13 (n 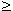 0) и рис.14 (n < 0). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:
0) и рис.14 (n < 0). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:
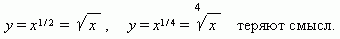
 .
.
Обратная функция
Обра́тная фу́нкция - функция, обращающая зависимость, выражаемую данной функцией. Функция 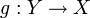 является обратной к функции
является обратной к функции 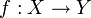 , если выполнены следующие тождества:
, если выполнены следующие тождества: 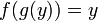 для всех
для всех 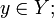
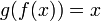 для всех
для всех 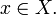
Предел функции в точке. Основные свойства предела.
Корень n-ой степени и его свойства.
Корнем n-ой степени из числа a называется такое число, n-ая степень которого равна a.
Определение: Арифметическим корнем n-ой степени из числа a называют неотрицательное число, n-ая степень которого равна a.
Основные свойства корней:
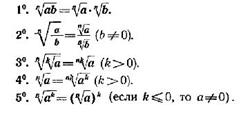
Степень с произвольным действительным показателем и его свойства.
Пусть дано положительное число 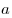 и произвольное действительное число
и произвольное действительное число 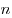 . Число
. Число 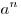 называется степенью, число
называется степенью, число 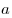 - основанием степени, число
- основанием степени, число 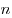 - показателем степени.
- показателем степени.
По определению полагают:
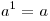 .
.
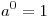 .
.
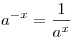 ,
, 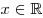 .
.
Если 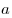 и
и 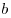 - положительные числа,
- положительные числа, 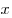 и
и 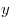 - любые действительные числа, то справедливы следующие свойства:
- любые действительные числа, то справедливы следующие свойства:
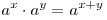 .
.
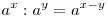 .
.
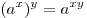 .
.
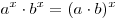 .
.
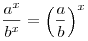 .
.
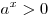 .
.
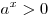
 2020-01-14
2020-01-14 477
477








